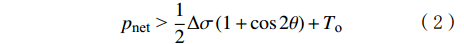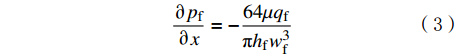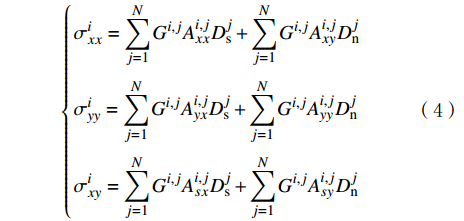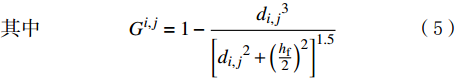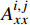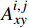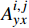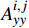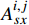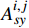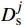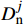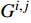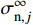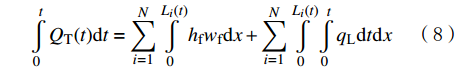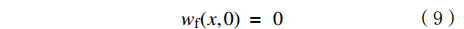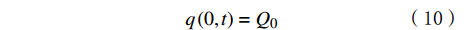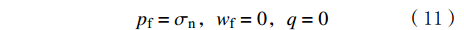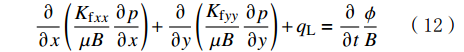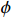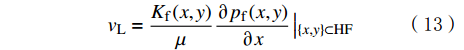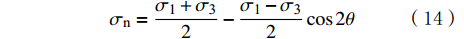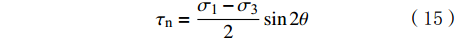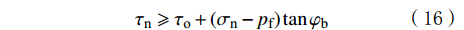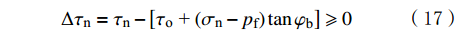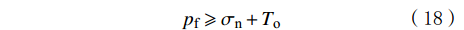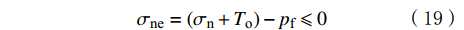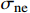Numerical Simulation of Complex Fracture Propagation in Shallow Shale Gas Fracturing in Zhaotong
-
摘要:
昭通浅层页岩气田主体埋深在1 000~2 200 m,地层压力系数低,效益开发难度较大,水力压裂是唯一增产措施,但目前国内尚无对中浅层页岩储层实施规模开发的经验可供借鉴,水力压裂工艺参数仍有优化空间。为明确目标昭通浅层页岩气田裂缝扩展主控影响因素,优化页岩气水平井压裂参数,针对该页岩气田储层天然裂缝发育、水平应力差小,主体改造工艺射孔簇较多等地质、工程特点,开展了昭通浅层页岩气压裂复杂裂缝扩展数值模拟研究。采用位移不连续法,考虑天然裂缝和水力裂缝的相互作用模式,基于压裂裂缝流动方程、裂缝宽度方程和物质平衡方程,推导了复杂裂缝扩展数学模型;针对昭通浅层页岩气实际地质特点,基于建立的数学模型优化了施工参数,明确了天然裂缝内聚力、射孔簇数是影响改造体积的主要因素。同时,通过暂堵数值模拟,明确得出:暂堵有利于提高裂缝开启效率,暂堵位置、暂堵时机及暂堵次数对暂堵效果有明显影响。通过现场试验对比模拟结果,发现采取优化后的压裂措施可使单井日产气量提高30.3%。该研究成果对昭通浅层页岩气后续压裂施工具有良好的借鉴意义。
Abstract:The main burial depth of the shallow shale gas field in Zhaotong is 1000-2200 m. The formation pressure coefficient is low, making the benefit development challenging. Hydraulic fracturing technology remains the only stimulation measure. However, there is no prior experience of large-scale development of medium and shallow shale reservoirs in China for reference. Therefore, there is still room for optimizing hydraulic fracturing parameters. In consideration of the geological and engineering characteristics, such as natural fracture development, small horizontal stress differences, and large perforation cluster numbers of the main stimulation, a numerical simulation of complex fracture propagation in shallow shale gas fracturing in Zhaotong was conducted. The displacement discontinuity method was employed, with the interaction mode of natural and hydraulic fractures considered. Based on the fracture flow equation, fracture width equation, and mass balance equation, the mathematical model of complex fracture propagation was derived. Based on the model, construction parameters were optimized according to the actual geological characteristics of shallow shale gas in Zhaotong. It was determined that natural fractures and perforation cluster numbers were the main factors affecting the stimulated reservoir volume (SRV). At the same time, through the temporary plugging numerical simulation, it is clarified that temporary plugging is conducive to improving the fracture opening efficiency, and the location, timing and times for temporary plugging have obvious effects on the temporary plugging effect. The simulation results were compared with on-site test results, demonstrating that the optimized fracturing measures increased daily single gas production by 30.3%. Consequently, this study provides valuable insights for the subsequent fracturing treatment of shallow shale gas in Zhaotong.
-
昭通浅层页岩气储层主要分布在五峰组—龙马溪组一段,主构造埋深1 000~2 200 m,整体可压性较高,脆性矿物含量高,且自上而下逐渐增高。页岩中的脆性矿物一般指石英、长石等碎屑岩矿物,方解石、白云石等碳酸盐类矿物,以及黄铁矿等。龙马溪组脆性指数均值60.67,最小水平主应力21.8~29.2 MPa(平均26.4 MPa),最大水平主应力30.0~37.7 MPa(平均34.7 MPa),水平应力差8.3 MPa[1–2]。储层内天然裂缝发育,垂向应力居中或最小,呈逆走滑断层地应力状态,部分区域极易形成水平裂缝,目前压裂采用以“小簇距+大排量”单段多簇(大于 5 簇)的改造模式,但多簇裂缝受地应力的影响,各簇开启难度不一,部分射孔簇进液效率低,限制了单井改造效果。为保证射孔簇均匀起裂,投入暂赌球,利用暂堵球封堵射孔孔眼,通过一次或多次暂堵转向,促进射孔簇均匀起裂,提高了各簇进液效率和作业效率。
已有研究表明,天然裂缝可能会改变水力裂缝的延伸路径,压裂裂缝性储层可能会形成多分支和非平面的复杂裂缝。室内试验发现,在一定的逼近角和应力差条件下,天然裂缝会改变水力裂缝的延伸路径[3]。近年来,不少研究者开始采用数值模拟方法研究天然裂缝对水力裂缝的影响[4–11],建立了水力裂缝非平面延伸的数学模型,讨论了水力裂缝沿天然裂缝延伸时天然裂缝宽度的变化规律。数值模拟表明,一定导流能力的网络裂缝对提高页岩气产量具有重要作用[12]。
对于暂堵材料在水平井中运移以及封堵机理的研究较少,目前矿场中评价暂堵的方法主要以现场施工暂堵后压力涨幅为主,具有较大的不确定性。郑新权等人[12]提出了暂堵转向有效性三参数评价方法:增压值(堵得住)、叠置正压差(堵得稳)、磨蚀压降(堵得准);周朗等人[13]建立了页岩气水平井段内多簇暂堵转向压裂裂缝动态扩展模型,实现了对暂堵前后分簇裂缝扩展形态的动态模拟;郭建春等人[14]通过对国内外文献进行总结,针对暂堵转向压裂技术,提出强化暂堵理论研究,明确暂堵剂运移、封堵、暂堵层承压和裂缝转向机理的发展建议;Tan Xuehao等人[15]修正了暂堵球运移数学模型,利用修正后的模型可以预测不同密度暂堵球在直井、斜井和水平井中的暂堵效率;A.Wilson[16]分析了暂堵机理,认为大颗粒暂堵剂暂堵后注入小颗粒暂堵剂能有效建立裂缝封堵体系;M. A. EL-EMAM等人[17]采用CFD+DEM耦合方法建立了水平内暂堵球运移封堵模型,分析了暂堵球粒径、暂堵球数量等对封堵效率的影响。
由于前人的研究主要集中于平面裂缝延伸模型,同时未考虑天然裂缝–地应力耦合条件下施工参数的优化,对于矿场应用推广性较低。因此,笔者将平面裂缝延伸模型扩展到二维复杂裂缝延伸数学模型,以期通过求解裂缝交点处的流体压力和裂缝宽度得到不同时间的裂缝几何尺寸。同时,针对目前国内外尚无相关软件或工具可以进行投球暂堵方式模拟及优化的现状,通过设置缝内暂堵体渗透率的方法,实现了缝内暂堵数值模拟,并开展了暂堵次数、暂堵位置及投入时机的优化研究。
1. 数学模型的建立
页岩储层压裂中复杂裂缝的形成过程,主要包括一个压裂段内多条主裂缝同步延伸、压裂流体滤失、储层孔隙压力升高、天然裂缝激活,以及天然裂缝激活导致储层渗透率增大和孔隙度变化。基于此,建立了页岩气压裂复杂裂缝扩展模型。
1.1 水力裂缝与天然裂缝相交扩展准则
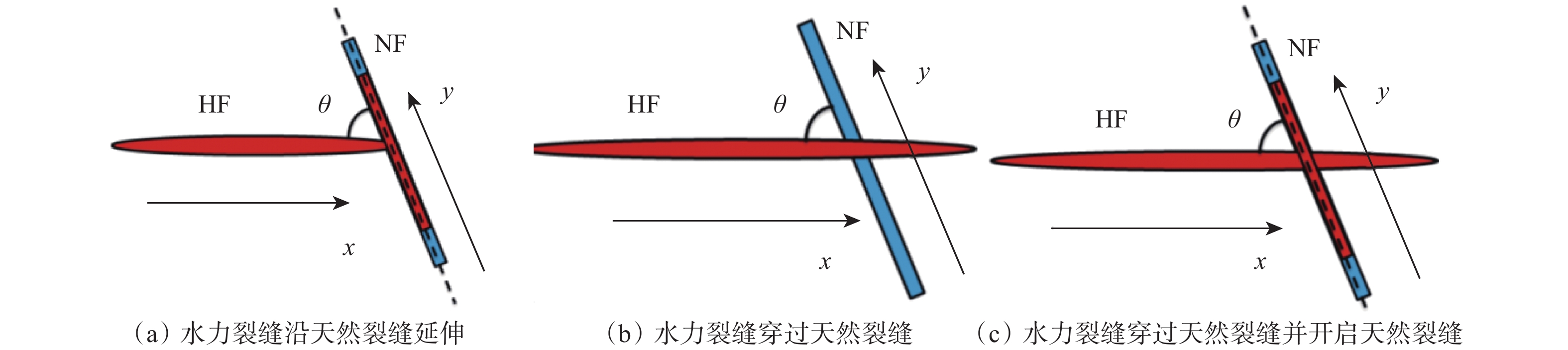
根据相关理论和试验结果,水力裂缝与天然裂缝相交后,水力裂缝存在3种扩展路径[17–18]:1)水力裂缝会开启闭合的天然裂缝并沿着天然裂缝转向延伸;2)水力裂缝穿过天然裂缝延伸,但是天然裂缝没有开启;3)水力裂缝穿过天然裂缝延伸并且开启天然裂缝(如图1所示,其中θ为天然裂缝与水平最大主应力的夹角(天然裂缝的逼近角),HF表示水力裂缝,NF表示天然裂缝),压裂流体可能沿着x和y方向流动(其中x方向为平行于水力裂缝方向,y方向为平行于天然裂缝方向)。
对于第一种延伸模式,满足的力学条件为:
12Δσ(1+cos2θ)+To>pnet > 12Δσ(1−cos2θ) (1) 对于第二种延伸模式,满足的力学条件为:
pnet > 12Δσ(1+cos2θ)+To (2) 式中:Δσ为水平主应力差,MPa;θ为天然裂缝的逼近角,(°);To为岩石的抗张强度,MPa;pnet为交点处水力裂缝净压力,MPa。
对于第三种延伸模式,需要交点处的净压力同时满足式(1)和式(2)。
1.2 缝中流体流动压降方程
流体在裂缝中沿着长度方向流动的压降方程为:
∂pf∂x=−64μqfπhfw3f (3) 式中:pf为水力裂缝内的流体压力,MPa;μ为压裂液黏度,mPa·s;qf为水力裂缝横截面的体积流量,m3/s ; hf为水力裂缝的高度,m;wf为水力裂缝的宽度,m。
1.3 水力裂缝宽度
对于分段多簇射孔的水平井,水力压裂过程中多条裂缝在一个压裂段之内同时延伸,延伸的水力裂缝之间互相干扰会影响水力裂缝的宽度。基于二维位移不连续理论引入三维修正因子[19],得到 x–y平面内任意单元i的法向与切向诱导应力:
{σixx=N∑j=1Gi,jAi,jxxDjs+N∑j=1Gi,jAi,jxyDjnσiyy=N∑j=1Gi,jAi,jyxDjs+N∑j=1Gi,jAi,jyyDjnσixy=N∑j=1Gi,jAi,jsxDjs+N∑j=1Gi,jAi,jsyDjn (4) 其中Gi,j=1−di,j3[di,j2+(hf2)2]1.5 (5) 任意单元j的边界条件可表示为:
{σjxy=0σjyy=pf,j−σ∞n,j(j=1,2,...,N) (6) 式中:
Ai,jxx ,Ai,jxy ,Ai,jyx ,Ai,jyy ,Ai,jsx 和Ai,jsy 为平面应变弹性系数,可以通过文献得到;Djs 和Djn 分别为裂缝单元j微段上的剪切和正位移不连续量,m;Gi,j 为三维修正因子;di,j为单元i到裂缝单元j的距离,m;N为裂缝单元数量;σ∞n,j 为裂缝面的正应力,MPa。将式(6)中应力边界条件代入式(4),可求出任意裂缝单元的正位移不连续量和剪切位移不连续量,其中正位移不连续量为裂缝宽度。
1.4 物质平衡方程
注入流体一部分用于扩展裂缝体积,一部分滤失到天然裂缝中,故而单条水力裂缝流体的质量守恒方程为:
∂q∂x+qL+∂(wfhf)∂t=0 (7) 全局物质守恒方程为:
t∫0QT(t)dt=N∑i=1Li(t)∫0hfwfdx+N∑i=1Li(t)∫0t∫0qLdtdx (8) 式中:qL为压裂液滤失体积,m2/s;QT(t)为压裂液注入排量,m3/s;Li(t)为t时刻第i条裂缝的长度,m。
1.5 初始条件和边界条件
初始条件下裂缝的宽度为0,即:
wf(x,0)=0 (9) 井筒注入点处的排量恒定:
q(0,t)=Q0 (10) 在裂缝端点处:
pf=σn,wf=0,q=0 (11) 式中:σn为裂缝表面的正应力,MPa。
1.6 天然裂缝流动方程
水力裂缝激活天然裂缝之后,压裂液大量流入储层中,引起储层孔隙压力急剧升高[20]。单相微可压缩流体在储层中流动的质量守恒方程为:
∂∂x(KfxxμB∂p∂x)+∂∂y(KfyyμB∂p∂y)+qL=∂∂tϕB (12) 式中:B为压裂液的体积系数;pr为储层孔隙压力,MPa;
ϕ 为储层孔隙度(其值将随天然裂缝破坏而增大);Kfxx和Kfyy为裂缝沿着x和y两个方向的渗透率,D。1.7 压裂液滤失
水力裂缝中的流体在水力裂缝与储层压差作用下,压裂液大量滤失进入储层天然裂缝系统中。考虑流体由水力裂缝垂直线性渗入天然裂缝系统中,基于达西定律可以得到滤失量为[21]:
vL=Kf(x,y)μ∂pf(x,y)∂x|{x,y}⊂HF (13) 式中:vL为滤失速度,m/s;Kf(x,y)为储层渗透率,D。
1.8 天然裂缝破坏准则
天然裂缝发育是低渗透油气藏储层压裂形成复杂裂缝网络的必要条件。天然裂缝是储层力学上的薄弱环节,压裂改造过程中天然裂缝更易先于基岩发生张开和剪切破裂[19],有利于复杂裂缝网络的形成。作用在天然裂缝面上的正应力和剪应力可以通过二维应力解得到,表达式为:
σn=σ1+σ32−σ1−σ32cos2θ (14) τn=σ1−σ32sin2θ (15) 式中: τn为裂缝上的剪切应力,MPa;σ1,σ3分别为最大和最小水平应力,MPa。
天然裂缝中孔隙流体压力的升高将会使天然裂缝面自身的力学强度降低,致使作用在天然裂缝平面上的剪切应力大于裂缝面的剪切强度,根据Mohr–Coulomb准则,天然裂缝发生剪切滑动的条件为:
τn⩾ (16) 由式(16)得到:
\Delta {\tau _{\text{n}}} = {\tau _{\text{n}}} - \left[ {{\tau _{\text{o}}}{\text{ + }}({\sigma _{\text{n}}} - {p_{\text{f}}})\tan {{\varphi _{{\text{b}}}}} } \right] \geqslant 0 (17) 式中:τo为天然裂缝的内聚力,MPa;φba为天然裂缝的内摩擦角,(°);Δτn为有效剪应力,MPa。
如果天然裂缝系统中流体压力持续升高,直至超过垂直作用在天然裂缝面上的正应力和抗拉强度时,天然裂缝发生张性破坏,张开破裂准则的数学表达式为[22–23]:
{p_{\text{f}}} \geqslant {\sigma _{\text{n}}} + {T_{\text{o}}} (18) {\sigma _{{\text{ne}}}} = \left( {{\sigma _{\text{n}}} + {T_{\text{o}}}} \right) - {p_{\text{f}}} \leqslant 0 (19) 式中:
\sigma_{{\rm{ne}}} 为裂缝的有效正压力,MPa。Δτn>0代表该区域内的天然裂缝发生剪切破裂,σne<0则代表该区域内的天然裂缝发生张开破裂,因此可将Δτn>0和σne<0的总区域等效为增产区域。
2. 敏感性分析
根据前面建立的复杂裂缝模拟数学模型,模拟天然裂缝发育条件下天然裂缝参数和施工参数对储层改造体积(SRV)的影响,基本参数设置如下:天然裂缝平均倾角88°,天然裂缝平均逼近角65°,天然裂缝内聚力0~1 MPa,内摩擦角30°;地层杨氏模量35~45 GPa,泊松比0.24,最大水平主应力44~51 MPa,最小水平主应力32~40 MPa,垂向应力37 MPa。
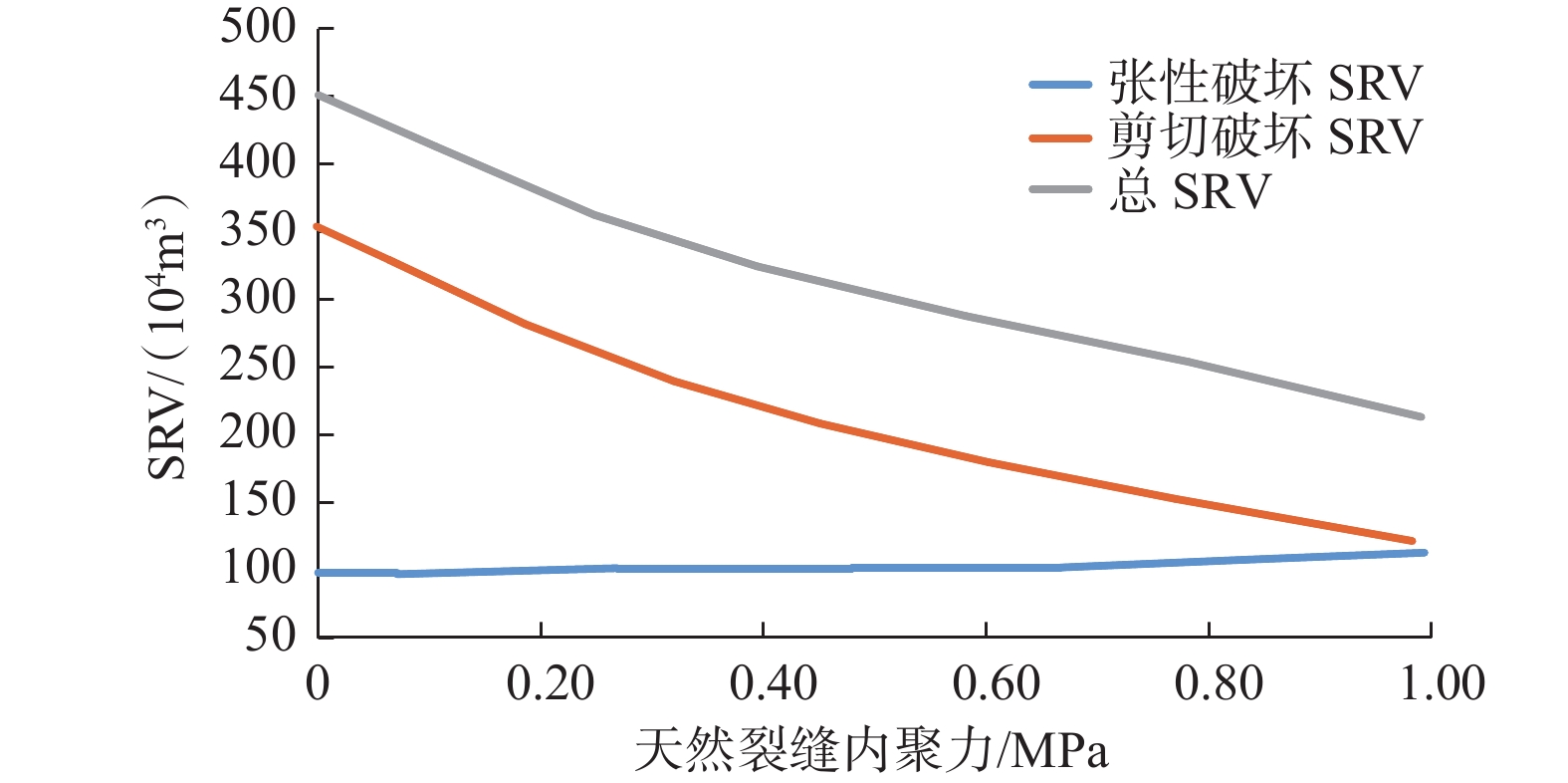
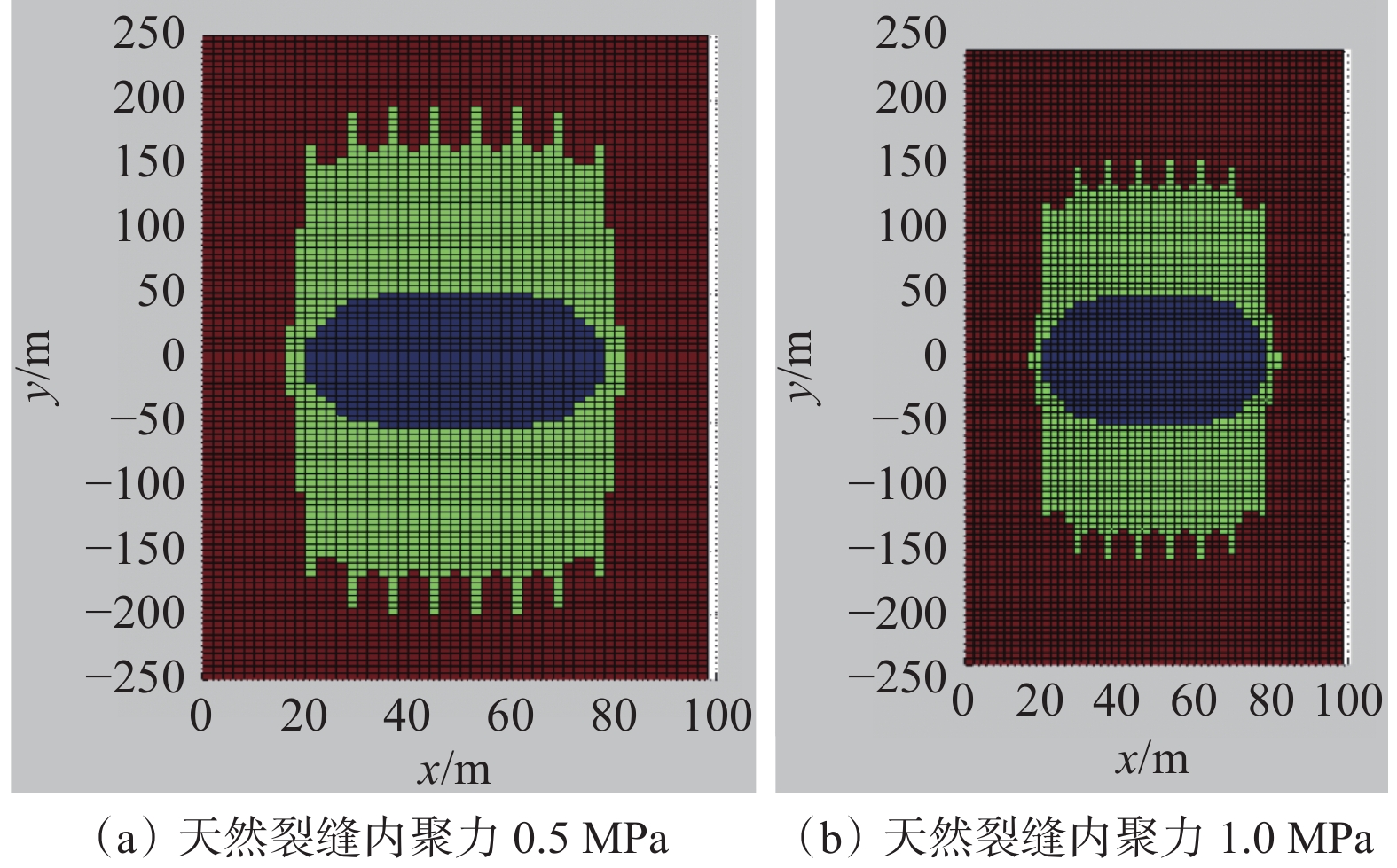
2.1 天然裂缝内聚力
图2所示为天然裂缝内聚力对SRV的影响,图3(a)和图3(b)分别表示内聚力分别为0.5和1.0 MPa时发生张性破坏和剪切破坏的区域。从图2、图3可以看出,内聚力对天然裂缝张性破坏SRV基本没有影响,但是剪切破坏 SRV随着内聚力增大而大幅度减小,最终导致总SRV逐渐减小。这是因为,天然裂缝内聚力越大,天然裂缝越不容易发生剪切破坏,但内聚力对天然裂缝张性破坏并没有影响,所以张性破坏SRV不变。
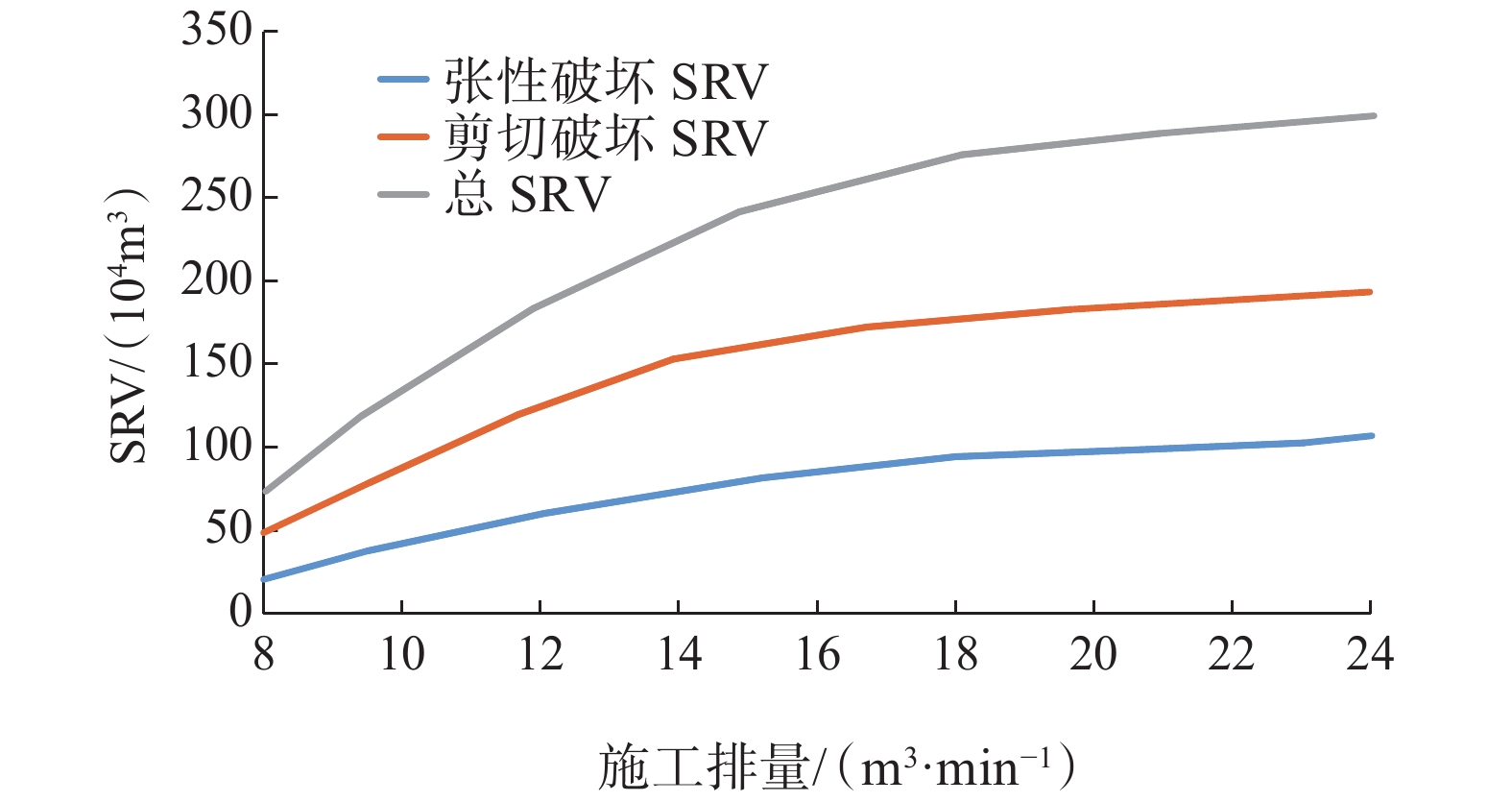
2.2 泵注排量
图4所示为泵注排量对SRV的影响,图5(a)和图5(b)分别表示泵注排量为12和18 m3/min时储层的总改造区域。从图4可以看出,张性破坏SRV、剪切破坏SRV和总SRV随着泵注排量增大而增大,但是增大幅度逐渐减小,泵注排量在18 m3/min左右时最优。从图5可以看出,泵注排量18 m3/min改造区域的长度明显比泵注排量12 m3/min长。这是因为,随着泵注排量增大,水力裂缝内净压力升高,水力裂缝容易穿过天然裂缝实现深穿透。此外,泵注排量增大也使天然裂缝内的孔隙压力显著升高,促使天然裂缝发生张性破坏与剪切破坏,因此更有利于 SRV增大。
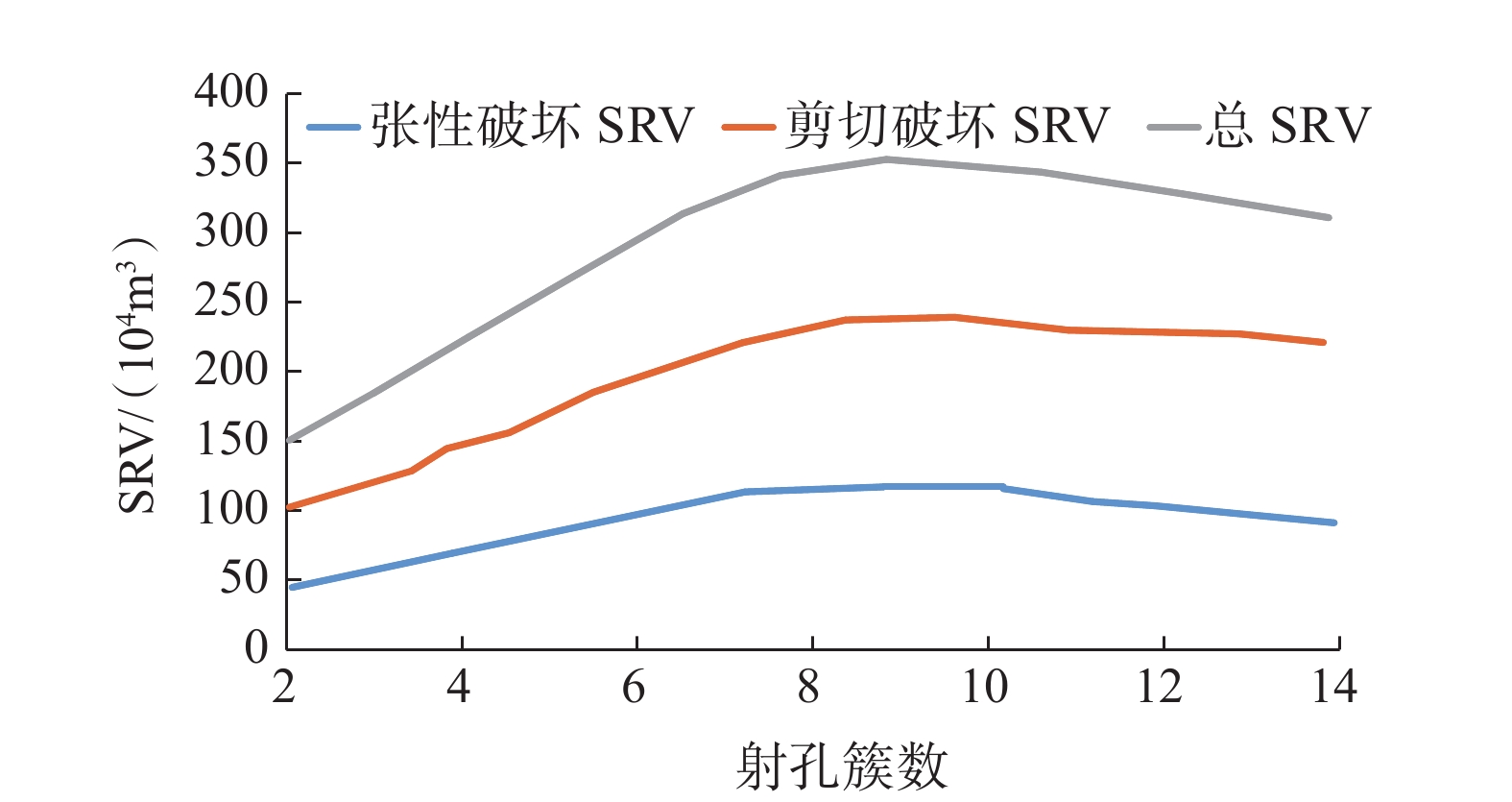
2.3 射孔簇数
图6和图7所示为射孔簇数对SRV影响的模拟结果。从图6和图7可以看出,张性SRV、剪切SRV及总SRV随射孔簇数增多先增大后减小。这是由于泵注排量保持不变的条件下,射孔簇数较少时,单簇排量增加,缝内净压力升高有利于水力裂缝实现深穿透,形成长度较长的裂缝,但是总SRV较小,这是由于单簇进液量增加,各簇之间的SRV可能重叠导致重复改造;但是当射孔簇数过多时,单簇进液量降低,缝内净压力降低,不利于主裂缝周围天然裂缝发生剪切和张性破坏,改造区域扩展长度减小,总 SRV减小。因此,存在最优射孔簇数,本例中最优射孔簇数在7~9簇。
2.4 暂堵时机优化模拟
为明确不同暂堵时机下裂缝扩展的规律,分别开展了在泵注1/3总液量和2/3总液量时暂堵后裂缝形态的模拟,结果如图8所示。由图8可知,在暂堵位置相同条件下,在施工早期暂堵有利于提高缝内压力,促进天然裂缝激活开启;暂堵时机选择越晚,流体滤失量越大,主裂缝延伸越长,对开启天然裂缝不利。
2.5 暂堵次数
分别模拟了缝内暂堵1次和2次后的裂缝形态,结果如图9所示。由图9可知:缝内暂堵后,沿着水力裂缝延伸方向天然裂缝逐渐开启,靠近井筒附近天然裂缝成为优势通道,天然裂缝开启较长;第2次暂堵近井筒附近天然裂缝,水力裂缝延伸方向天然裂缝均匀扩展,提高了远井地带裂缝的复杂程度。
2.6 水平应力差
水平应力差是影响裂缝起裂的关键参数(见图10),昭通浅层页岩气田储层的应力差异较大,导致射孔簇开启效率不高,数值模拟得出:水平应力差越大,水力裂缝缝内暂堵后开启天然裂缝所需流体压力越高,缝内暂堵转向越困难。分析其原因,认为最大水平应力越大,天然裂缝缝面正应力越大,天然裂缝张性开启越困难。
3. 现场试验
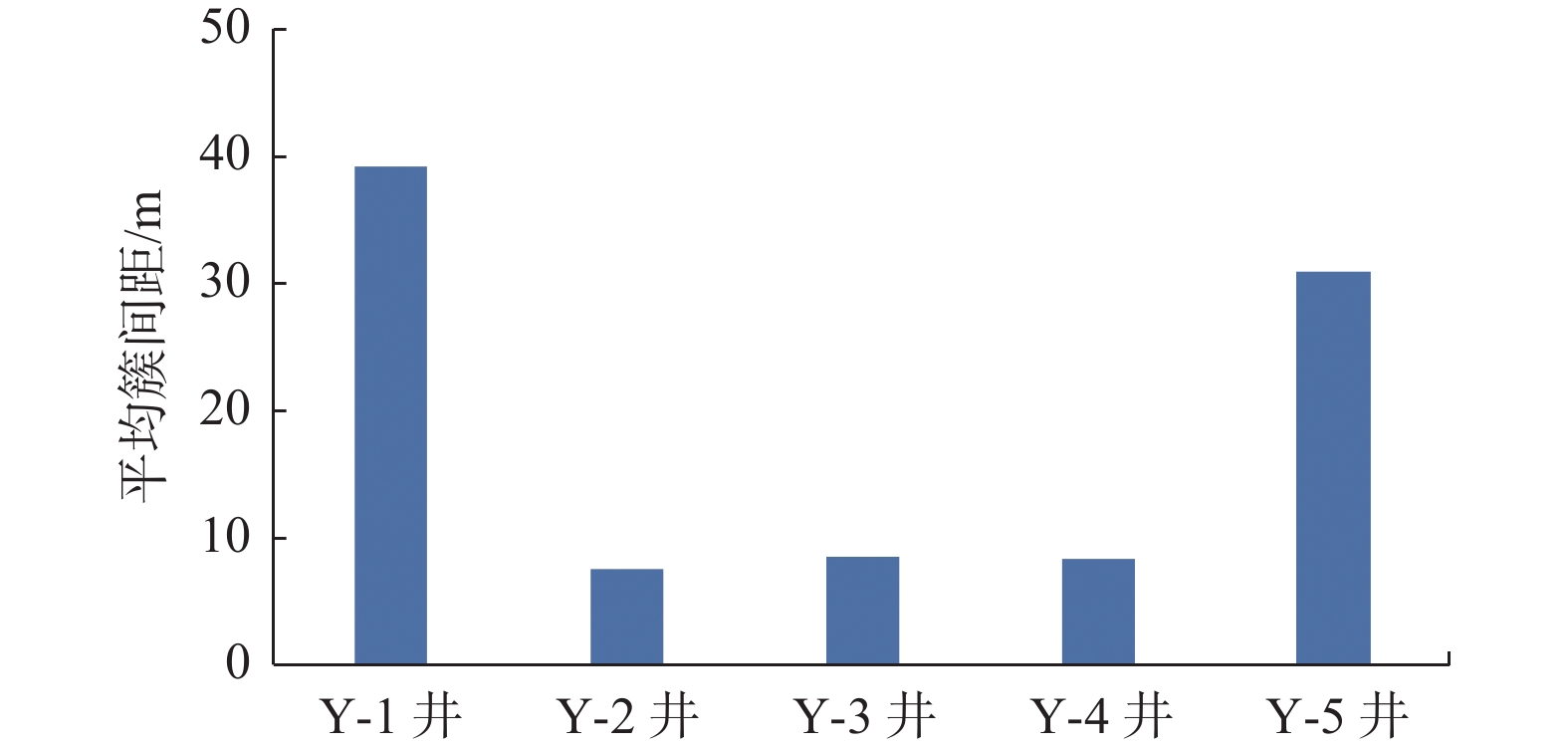
为验证模拟结果的可靠性,在昭通页岩气太阳–大寨示范区的阳102H16平台开展了现场试验。该平台储层杨氏模量均值38 GPa,泊松比均值0.22,最小水平应力均值35 MPa,水平应力差值8.4 MPa。针对天然裂缝以及断层等地质异常对页岩压裂影响大的问题,结合数值模拟预测结果,根据该平台天然裂缝与井筒位置关系不同制定了针对性的压裂方案,在加砂强度和用液强度基本一致的情况下对比了5口井的簇间距,结果如图11所示(阳 102H16-1井 简写为Y-1井,其他同理)。
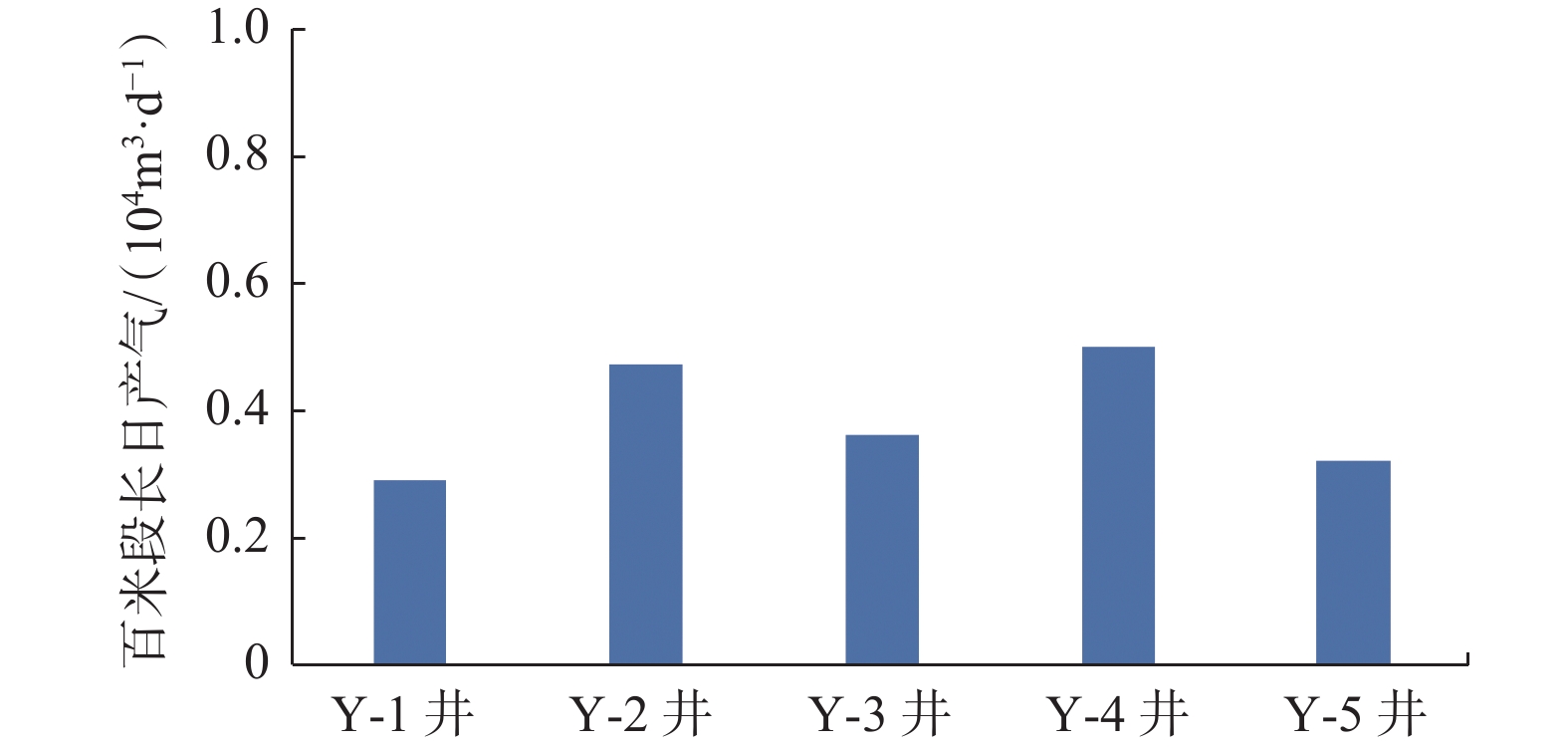
对于图11中5口井,从生产数据看,多射孔簇井平均日产气量2.67×104 m3,少射孔簇井平均日产气量2.26×104 m3,多射孔簇井比少射孔簇井平均日产气高18.14%;多射孔簇井(Y-2井、Y-3井和Y-4井)平均折算百米日产气0.443×104 m3,少射孔簇井(Y-1井、Y-5井)平均折算百米日产气0.305×104 m3(见图12),多射孔簇井比少射孔簇井平均折算百米日产气高45.25%;少射孔簇2口井的套压低于多射孔簇的3口井,表明射孔簇数多裂缝开启效率较高,人工裂缝导流能力较高;少射孔簇井裂缝半长可能长,但缝网复杂程度较低,造成产量差异。
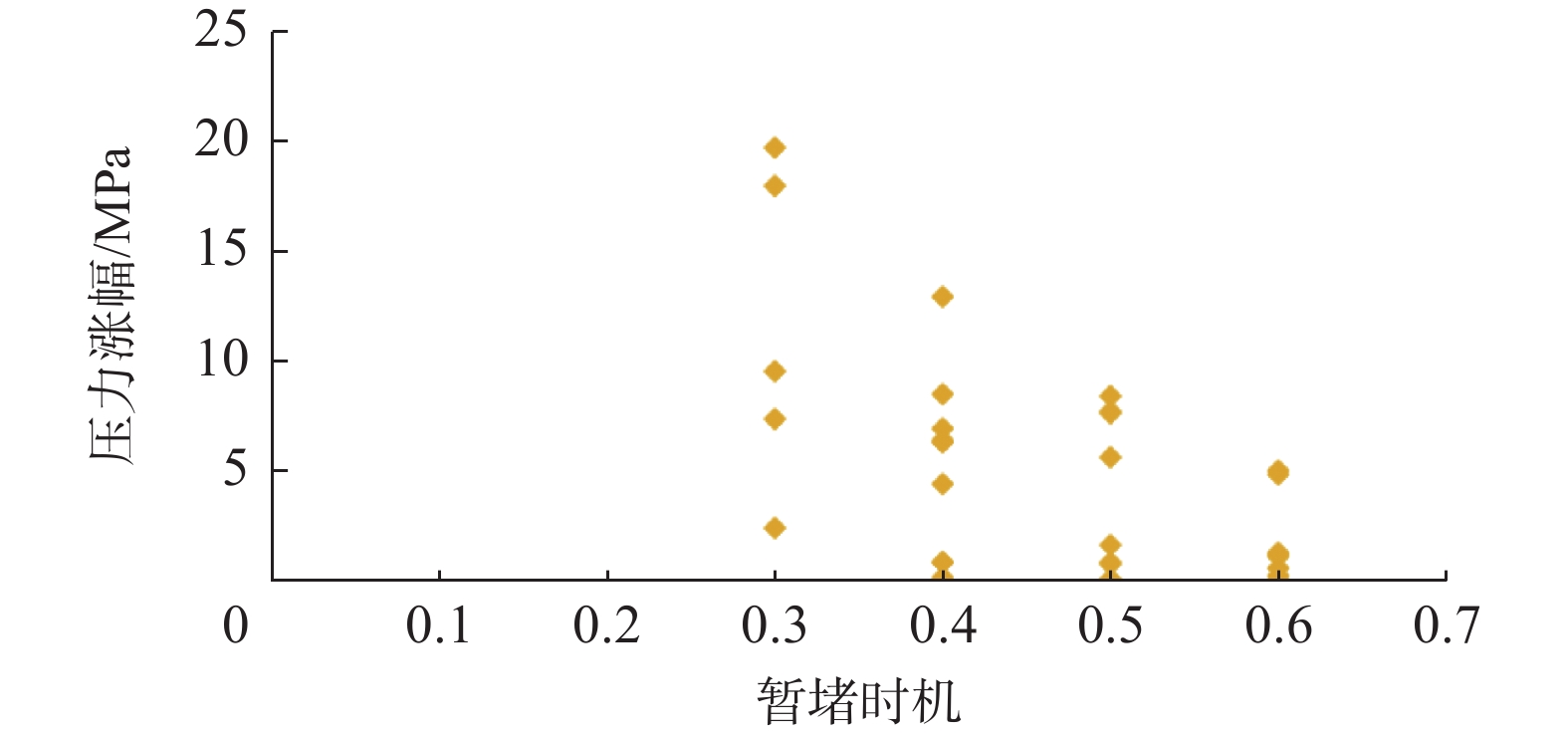
在本平台开展了暂堵优化试验,结果如图13所示。从暂堵压力响应来看,提早暂堵有利于防止裂缝过度延伸,提高开启效率,但平台内未部署微地震监测,仅能从压力涨幅和暂堵前后施工压力曲线叠加判断暂堵效果。
4. 结 论
1)将平面裂缝延伸模型扩展为二维复杂裂缝延伸模型,模拟了天然裂缝发育下的人工裂缝扩展规律,发现天然裂缝内聚力越小,储层改造体积越大。
2)模拟结果显示,天然裂缝内聚力越小,页岩压裂的SRV越大。压裂昭通浅层页岩气储层时,注入排量16~18 m3/min、单段射孔8簇左右时容易形成复杂缝网。
3)现场试验进一步明确了增加射孔簇数和提早进行暂堵,可以防止裂缝过度延伸、提高开启效率、增大储层改造体积、提高单井产量。
4)多射孔簇下改造容易造成射孔簇流量分配不均匀等问题,需要与暂堵工艺配合来改善改造效果。本研究对暂堵方案(暂堵时机、暂堵次数等)做了进一步优化模拟,形成了昭通浅层页岩气压裂改造施工模板。
-
-
[1] 徐政语,梁兴,鲁慧丽,等. 昭通示范区五峰组—龙马溪组页岩气成藏类型与有利区分布[J]. 海相油气地质,2021,26(4):289–298. XU Zhengyu, LIANG Xing, LU Huili, et al. Shale gas accumulation types and favorable area distribution of Wufeng Formation-Longmaxi Formation in Zhaotong Demonstration Area[J]. Marine Origin Petroleum Geology, 2021, 26(4): 289–298.
[2] 王红岩,刘钰洋,张晓伟,等. 基于层次分析法的页岩气储层地质工程一体化甜点评价:以昭通页岩气示范区太阳页岩气田海坝地区X井区为例[J]. 地球科学,2023,48(1):92–109. WANG Hongyan, LIU Yuyang, ZHANG Xiaowei, et al. Geology-engineering intergration shale gas sweet spot evaluation based on analytic hierarchy process: application to Zhaotong Shale Gas Demonstration District, Taiyang Shale Gas Field, Haiba Area, X Well region[J]. Earth Science, 2023, 48(1): 92–109.
[3] RAHMAN M M, AGHIGHI A, RAHMAN S S. Interaction between induced hydraulic fracture and pre-existing natural fracture in a poro-elastic environment: effect of pore pressure change and the orientation of natural fracture[R]. SPE 122574, 2009.
[4] TALEGHANI A D, OLSON J E. How natural fractures could affect hydraulic-fracture geometry[J]. SPE Journal, 2014, 19(1): 161–171. doi: 10.2118/167608-PA
[5] CHENG Wan, JIN Yan, CHEN Mian, et al. Reactivation mechanism of natural fractures by hydraulic fracturing in naturally fractured shale reservoirs[J]. Journal of Natural Gas Science and Engineering, 2015, 27(Part 3): 1357 − 1365.
[6] AIMENE Y, HAMMERQUIST C, OUENES A. Anisotropic damage mechanics for asymmetric hydraulic fracture height propagation in a layered unconventional gas reservoir[J]. Journal of Natural Gas Science and Engineering, 2019, 67: 1–13. doi: 10.1016/j.jngse.2019.04.013
[7] 赵金洲,任岚,胡永全,等. 裂缝性地层水力裂缝非平面延伸模拟[J]. 西南石油大学学报(自然科学版),2012,34(4):174–180. ZHAO Jinzhou, REN Lan, HU Yongquan, et al. Numerical simulation on non-planar propagation of hydraulic fracture in naturally fractured formations[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2012, 34(4): 174–180.
[8] RU Zhixing, HU Jinghong, MADNI A S, et al. A study on the optimal conditions for formation of complex fracture networks in fractured reservoirs[J]. Journal of Structural Geology, 2020, 135: 104039. doi: 10.1016/j.jsg.2020.104039
[9] GUO Jianchun, ZHAO Xing, ZHU Haiyan, et al. Numerical simulation of interaction of hydraulic fracture and natural fracture based on the cohesive zone finite element method[J]. Journal of Natural Gas Science and Engineering, 2015, 25: 180–188. doi: 10.1016/j.jngse.2015.05.008
[10] DAHI-TALEGHANI A, OLSON J E. Numerical modeling of multistranded - hydraulic - fracture propagation: accounting for the interaction between induced and natural fractures[J]. SPE Journal, 2011, 16(3): 575–581. doi: 10.2118/124884-PA
[11] CIPOLLA C L, LOLON E P, ERDLE J C, et al. Reservoir modeling in shale-gas reservoirs[J]. SPE Reservoir Evaluation & Engineering, 2010, 13(4): 638–653.
[12] 郑新权,何春明,杨能宇,等. 非常规油气藏体积压裂2.0工艺及发展建议[J]. 石油科技论坛,2022,41(3):1–9. ZHENG Xinquan, HE Chunming, YANG Nengyu, et al. Volume fracturing 2.0 technology and development suggestions for unconventional reservoirs[J]. Petroleum Science and Technology Forum, 2022, 41(3): 1–9.
[13] 周朗,林然,周小金,等. 页岩气水平井段内多簇缝口暂堵转向压裂数值模拟[J]. 钻采工艺,2023,46(4):82–87. ZHOU Lang, LIN Ran, ZHOU Xiaojin, et al. Numerical simulation research on diverting fracturing for staged fracturing horizontal well in shale gas reservoir[J]. Drilling and Production Technology, 2023, 46(4): 82–87.
[14] 郭建春,赵峰,詹立,等. 四川盆地页岩气储层暂堵转向压裂技术进展及发展建议[J]. 石油钻探技术,2023,51(4):170–183. GUO Jianchun, ZHAO Feng, ZHAN Li, et al. Progress and development suggestions on temporary plugging and diversion fracturing technology for shale gas reservoirs in Sichuan Basin[J]. Petroleum Drilling Techniques, 2023, 51(4): 170–183.
[15] TAN Xuehao, WENG Xiaowei, AHMED T K, et al. An improved ball sealer model for well stimulation[R]. SPE189573, 2018.
[16] WILSON A. Engineering approach to designing fluid diverters: jamming and plugging[J]. Journal of Petroleum Technology, 2018, 70(6): 63–67. doi: 10.2118/0618-0063-JPT
[17] EL-EMAM M A, ZHOU L, SHI W, et al. Theories and applications of CFD-DEM coupling approach for granular flow: a review[J]. Archives of Computational Methods in Engineering, 2021, 28(7): 4979–5020. doi: 10.1007/s11831-021-09568-9
[18] REN Long, SU Yuliang, ZHAN Shiyuan, et al. Modeling and simulation of complex fracture network propagation with SRV fracturing in unconventional shale reservoirs [J]. Journal of Natural Gas Science and Engineering,2016,28:132-141
[19] 王军磊,贾爱林,位云生,等. 基于复杂缝网模拟的页岩气水平井立体开发效果评价新方法:以四川盆地南部地区龙马溪组页岩气为例[J]. 天然气工业,2022,42(8):175–189. WANG Junlei, JIA Ailin, WEI Yunsheng, et al. A new method for evaluating tridimensional development effect of shale gas horizontal wells based on complex fracture network simulation: A case study of Longmaxi Formation shale gas in the southern Sichuan Basin[J]. Natural Gas Industry, 2022, 42(8): 175–189.
[20] GHASSEMI A, ZHOU X X, RAWAL C. 3D poroelastic analysis of rock failure around a hydraulic fracture[J]. Journal of Petroleum Science and Engineering, 2013, 108(34/35): 118–127.
[21] LI Zhiqiang, QI Zhilin, YAN Wende, et al. New algorithm to simulate fracture network propagation using stationary and moving coordinates in naturally fractured reservoirs[J]. Energy Science & Engineering, 2020, 8(11): 4025–4042.
[22] HU Yongquan, LI Zhiqiang, ZHAO Jinzhou, et al. Prediction and analysis of the stimulated reservoir volume for shale gas reservoirs based on rock failure mechanism[J]. Environmental Earth Sciences, 2017, 76(15): 546–559.
[23] 林然. 页岩压裂水平井SRV动态模拟的理论研究[D]. 成都: 西南石油大学, 2018. LIN Ran. Dynamic simulation of stimulated reservoir volume(SRV) during hydraulic fracturing in horizontal shale gas well[D]. Chengdu: Southwest Petroleum University, 2018.
-
期刊类型引用(8)
1. 李紫妍,陈军斌,左海龙,王庆,欧阳雯,林天,刘波,任大忠. 页岩储层水力裂缝和天然裂缝交互规律. 断块油气田. 2024(02): 232-240 .  百度学术
百度学术
2. 尹帅,赵军辉,刘平,沈志成. 裂缝性储层天然缝与水力缝开启条件及扩展规律研究. 石油钻探技术. 2024(03): 98-105 .  本站查看
本站查看
3. 宋兆辉. 树莓状聚合物纳微米封堵剂的制备及性能评价. 石油钻探技术. 2024(03): 84-90 .  本站查看
本站查看
4. 刘善勇,尹彪,楼一珊,张艳. 粗糙裂缝内支撑剂运移与展布规律数值模拟. 石油钻探技术. 2024(04): 104-109 .  本站查看
本站查看
5. 史小卫,孙麒涵,陈俊侠,林萌,吴会永,王洪建. 首山一矿水平井水力压裂应力阴影效应及裂缝演化机理. 能源与环保. 2024(08): 14-21 .  百度学术
百度学术
6. 余绍志,纪国法. 基于水力压裂裂缝扩展规律的天然气开发应用. 能源与环保. 2024(08): 242-247+253 .  百度学术
百度学术
7. 李德旗,刘春亭,朱炬辉,胥云,王荣,张俊成,吴凯,潘丹丹. 高闭合压力下深层页岩气促缝网强支撑压裂工艺. 石油钻采工艺. 2024(03): 336-345 .  百度学术
百度学术
8. 杨亚东,邹龙庆,王一萱,朱静怡,李小刚,熊俊雅. 川南深层页岩气藏压裂裂缝导流能力影响因素分析. 特种油气藏. 2024(05): 162-167 .  百度学术
百度学术
其他类型引用(0)



 下载:
下载: