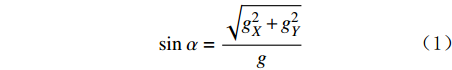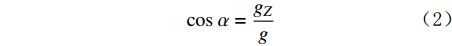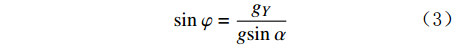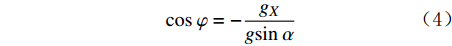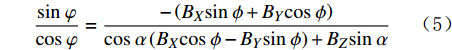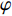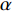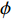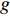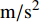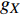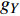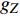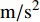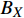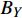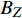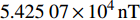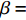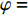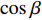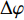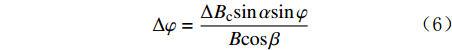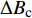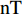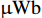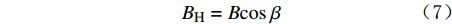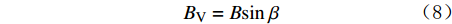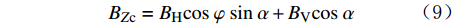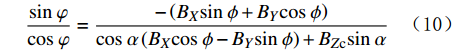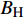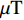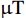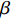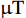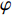Calculation and Correction of Azimuth Errors Based on Finite Element Analysis
-
摘要:
为了满足定向井磁方位的高精度需求,需要准确计算方位角测量误差和分析误差来源。采用有限元分析软件,模拟了钻具在地磁场中产生的干扰磁场的变化情况。通过钻杆内部三轴磁感应强度得出方位角误差的测量值,与钻杆真实方位对比得到了方位角误差。通过控制钻杆方位角、井斜角、底部钻具组合、无磁钻铤长度、外部磁场的大小和方向等因素,来观测、分析了方位角误差的变化规律。模拟试验得出,方位角误差在钻杆的南北方向上最小,在钻杆的东西方向上最大,并随着井斜角增大而增大,这种变化呈现出正弦的变化规律;经度、纬度也会对方位角的变化产生影响,方位角误差大体上随着维度增加而增大,主要取决于当地的总磁场和磁倾角大小。研究结果表明,方位角误差与测斜数据、底部钻具组合、经度、纬度和无磁钻铤长度有密切关系,可以通过有限元模拟准确估算出不同情况下方位角误差的大小,对方位角误差进行修正。模拟结果可为工程应用中无磁钻铤、底部钻具组合的选取和方位角误差修正提供参考数据和理论依据。
Abstract:The high-precision magnetic azimuth of directional wells requires the accurate calculation of azimuth measurement errors and analysis of error sources. In this study, the finite element analysis (FEA) software was used to simulate the change in the interference magnetic field generated by the drill tool in the geomagnetic field. The measured azimuth error was obtained through the triaxial magnetic induction intensity inside the drill pipe and was compared with the real azimuth of the drill pipe to get the azimuth error. Then, the variation laws of azimuth errors was observed and analyzed by controlling factors including the azimuth of the drill pipe, deviation angles, bottom hole assembly (BHA), non-magnetic drill collar length, and the size and direction of the external magnetic field. The simulation test showed that the azimuth error was the smallest in the north-south direction and the largest in the east-west direction of the drill pipe, and it increased with the rise in the deviation angles, which presented a sinusoidal variation law. Longitude and latitude would also affect the change in azimuth, and the azimuth error grew with the increase in dimensions in general and mainly depended on the local total magnetic field and magnetic inclination. The research results indicate that the azimuth error closely correlates with the inclinometer data, BHA, longitude, latitude, and the non-magnetic drill collar length, and it can be accurately estimated by finite element simulation under different conditions and then be corrected accordingly. The simulations can provide a reference and theoretical basis for the selection of the non-magnetic drill collar and BHA, and the correction of azimuth errors in engineering applications.
-
利用磁力随钻测斜仪(如MWD工具)实时测量井眼轨迹时[1-2],由于铁磁性钻具材料在地磁场作用下发生磁化而产生干扰磁场,对磁力测斜仪精度产生影响而导致方位角测量结果不准确[3-4]。目前,通常采用井眼测量精度行业指导委员会(ISCWSA)提供的误差模型[5],但ISCWSA的误差模型是基于现场实际测量数据所给定的参考值,而钻具的磁化受很多因素影响[6],在所有情况下都使用同一套数据显然是不准确的[7]。而且,随着各种测井工具和旋转导向工具的发展[8],ISCWSA所提供的磁极强度指导数据并不能涵盖所有类型;不同公司使用不同标准的磁性材料,也给井底钻具组合干扰磁场的计算带来了难度。简而言之,对于各种情况下的磁干扰,根据同一套标准去计算方位角,导致计算结果不可靠[9-10]。
针对钻具磁干扰引起的方位角误差,可通过增加无磁钻铤长度来减小传感器位置的干扰磁场,以减小方位角计算误差,也可以通过校正算法来校正磁干扰造成的误差。其中,使用无磁钻铤减小方位角误差时,要考虑无磁钻铤长度的设计问题,无磁钻铤过长会增加钻井成本,过短则不能有效消除误差。磁干扰校正算法主要分为轴向磁干扰校正和径向磁干扰校正[11]:径向磁干扰误差较小,在同一井深处旋转钻柱,测量仪器沿井眼估计轴线旋转并连续或者离散记录测量数据,径向磁干扰随钻柱旋转且与仪器坐标系相对静止,在径向磁干扰作用下,由磁通门径向连续或离散数据可确定出一个偏离坐标原点的圆,原点到圆心的距离便是径向磁干扰[12];轴向磁干扰校正方法有短箍校正法、罗素法、矢量和法和钻具截面法[13],都是通过地磁场和磁通门传感器的径向读数来消除轴向的误差;但在钻杆轴向磁场很小时(钻杆在东西向),地磁场在钻具轴向上的分量较小,对轴向上的磁场变化极为敏感,很小的钻具轴向磁干扰误差就会在地磁场方向引起很大的计算误差,导致计算方位角时产生误差,从而影响井眼轨迹计算的准确性[14]。所以,在方位角位于东/西20°范围内、井斜角超过70°的非非区不宜采用该方法,在高纬度地区非非区误差还会增大[15]。
针对上述问题,利用有限元方法,模拟分析了不同情况下的方位角误差和各个因素对方位角误差的影响规律。该方法打破了实验方法的局限性,考虑了更多的误差因素,并且可以灵活调整误差影响因素的数值,综合分析所有误差项,从而得到方位角误差模型。根据实际使用的钻具组合,设计不同的模型并选择相应的材料,可以突破ISCWSA误差模型的局限性,模拟出更准确的磁干扰误差,然后根据磁干扰的分布设计无磁钻铤的长度。传统校正方法在非非区计算误差很大,采用有限元模拟方法可以得到更准确的方位角测量误差。模拟结果可对实际生产中方位角计算、方位角修正和无磁钻铤长度选择提供数据参考和理论依据。
1. 方位角误差模型的建立及数据处理
1.1 模型的建立与参数设置
Ansys Maxwell[16]是一款基于麦克斯韦微分方程,采用有限元离散形式,将工程中电磁场问题转换为矩阵求解的软件。该软件是处理电磁问题的专业软件,具有高精度的自适应网格剖分功能、用户可自定义的材料库及强大的后处理功能。
钻杆和井底钻具组合本身带有一定磁性,在地磁场中会产生干扰磁场。而方位角通常通过测量三轴磁通量来计算得出,干扰磁场会使钻杆内部的磁通量发生变化,从而影响方位角的计算结果。为降低铁磁钻具对随钻磁力测斜仪的干扰,通常将随钻磁力测斜仪置于无磁钻铤中,但无磁钻铤上下部仍会产生干扰场,影响传感器位置的磁场。通过有限元模拟,可以准确计算出当前情况下干扰磁场的大小,从而计算出干扰磁场所产生的方位角误差。
井底钻具组合的结构、材料和外部地磁场分布是建立方位角误差模型的关键。其中,当地的地磁场强度、磁倾角和磁偏角,可根据具体井位信息通过NOAA(美国国家海洋和大气管理局)网站查得。磁场的磁倾角和磁偏角主要影响外部磁场的方向,由于铁磁材料具有电磁屏蔽效应,磁场与钻杆夹角的不同,会导致钻杆内部磁感应强度不同。外磁场垂直于钻杆轴向和平行于钻杆轴向时钻杆内部磁感应强度的分布情况如图1所示。
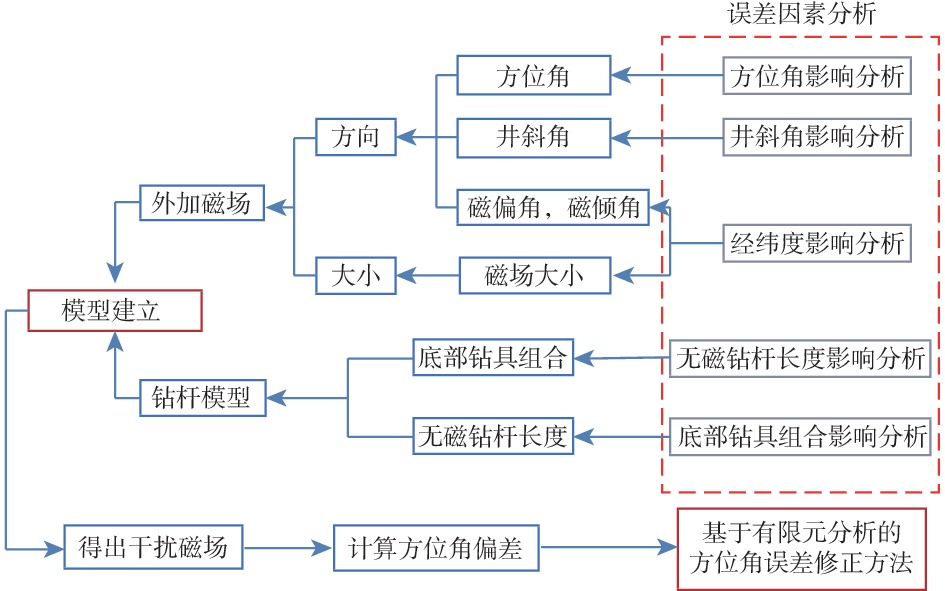
选取中国海油科技攻关项目“救援井关键技术研究及实钻工程示范”(编号:YJB18YF003)研究中的试验井(该井位于天津附近的渤海湾内),利用其钻具相关数据(见表1),建立了方位角误差模型,具体建模步骤如图2所示。
表 1 方位角误差模型采用的钻具数据Table 1. Data of drill tools used in the azimuth error model钻具或仪器 长度/mm 外径/mm PDC钻头 280 215.9 旋转导向工具 7 520 171.4 BCPM测井工具 4 940 171.4 集成井下测量仪 6 660 171.4 无磁钻铤 9 270 171.4 浮阀 680 165.1 加重钻杆 9 410 127.0 钻杆 9 410 127.0 1.2 数据分析与处理
通过上述有限元建模,可以得到传感器位置处的三轴磁感应强度。这些数据是基于仪器坐标系(O-XYZ)下的三轴磁感应强度数据,而通常是基于大地坐标系(O-NEV)描述井眼轨迹,仪器坐标系和大地坐标系可以通过井斜角、方位角和工具面角等参数相互转换[11-13]。
sinα=√g2X+g2Yg (1) cosα=gZg (2) sinφ=gYgsinα (3) cosφ=−gXgsinα (4) sinφcosφ=−(BXsinϕ+BYcosϕ)cosα(BXcosϕ−BYsinϕ)+BZsinα (5) 式中:
φ 为方位角,(°);α 为井斜角,(°);ϕ 为高边工具面角,(°);g 为重力加速度,m/s2 ;gX ,gY 和gZ 为X,Y和Z方向的重力加速度分量,m/s2 ;BX ,BY 和BZ 为磁场在为 X , Y 和 Z 方向的磁感应强度分量,µT。2. 方位角误差的影响因素
实测方位角误差主要受钻具的轴向磁干扰影响。产生钻具轴向磁干扰的因素包括钻具与地磁场的夹角和无磁钻铤上端、下端的磁极强度。井眼轨迹几何形态和地磁场方向决定着钻具与地磁场的夹角,地磁场方向与经度、纬度有关,井眼轨迹的几何形态与方位角和井斜角有关。无磁钻铤上、下端的磁极强度与井底钻具组合有关。基于此,分别分析了井眼轨迹方位角、井斜角、经度、纬度和底部钻具组合对实测方位角误差的影响。
2.1 井眼轨迹方位角的影响
保持外界磁场不变,旋转钻具模型,使井斜角分别为30°,60°和90°,导出钻具内部磁通门传感器位置处的磁场大小,使用该磁场数据计算出此时方位角测量值的大小,将方位角测量值与方位角设定值比较,得出方位角误差。外部磁场取试验井所在地区的地磁数据为:磁感应强度B=
5.42507×104nT ,磁倾角β= 58.1696°,磁偏角φ= −7.29°。将钻杆从方位角0°开始,依次旋转30°,直至330°,得到方位角误差随钻具摆放方位的变化情况,如图3所示。
由图3可知,方位角误差在钻具方位角为0°和180°时取得最小值,在90°和270°时取得最大值,即定向组件的方位测量误差越接近东西方向,误差越大;越接近南北方向,误差越小。
2.2 井眼轨迹井斜角的影响
为了验证轴向干扰磁场产生的方位误差与井斜角的关系,保持外部地磁场的大小和方向不变,设置钻杆方位分别为0°,30°,60°和90°,模拟了正北至正东方向的钻杆方位,在这些方位角下分别调整钻杆的倾斜角,记录测量点在模型内的测量值,计算不同井斜角下方位角的测量误差。方位角0°~90°时的误差随井斜角增大的变化如图4所示。
由图4可知,井斜角越接近水平方向时,轴向磁干扰对定向组件的方位测量值影响越大。
2.3 经度和纬度的影响
经度和纬度变化主要影响总磁场和磁倾角的变化。地球磁场在水平面的投影可以用
cosβ 表示,干扰磁场对定向组件方位测量的误差Δφ 可以表示为:Δφ=ΔBcsinαsinφBcosβ (6) 式中:
ΔBc 为干扰磁场磁感应强度的轴向分量,nT 。由此可以推论,井位的地理纬度越高时,磁倾角越大,轴向磁场干扰对方位测量的影响越大。定向组件在井斜角为90°、方位角为90°或270°时,钻具和地磁场的夹角最大,此时方位角的误差达到最大值。
选取天津地区的经度东经117.2°,改变纬度来观测纬度对方位角的影响。纬度从0°至北纬72°依次选取10个测点,采用有限元法模拟不同纬度下当地地磁场的状态,通过导出的磁场数据来计算方位角的测量值。由此得到不同纬度下方位角误差的变化情况,如图5所示。
由图5可知,随着纬度升高(磁倾角增大),钻具磁干扰对定向组件的影响越大,即在高纬度地区误差增长越快,这与之前的理论分析结果相吻合。
不同纬度下,方位角误差随钻杆方位的变化如图6所示。从图6也可以看出,高纬度地区方位角误差在急剧变大。
综合考虑经度和纬度进行试验。在北纬0°~60°,从西经160°每隔40°选取一个测点至东经160°(这些测点的范围基本覆盖了北半球的常见坐标),模拟该处地磁场强度下方位角误差的变化。不同经纬度下方位角误差的变化趋势如图7所示。
结合国际地磁参考场(international geomagnetic reference field,IGRF)[17],可以计算出不同经度、纬度下的地磁场和磁倾角,通过地磁场可以得到方位角随经度纬度变化的云图(见图8)。
由图8可知,方位角误差整体上随着纬度升高而增大,在某些磁异常地区方位角误差也会偏大,根据国际地磁参考模型结合有限元分析可以很好地估算出方位角误差。
2.4 井底钻具组合的影响
前面只讨论了地磁场对钻杆的磁化,但实际情况是,钻具组合所带的磁性会产生更大的干扰场(见图9,图中:PU,PL分别为无磁钻铤顶部和底部钻具的磁极强度,
μWb ,为计算方便,钻铤顶部磁场取向下为正方形,钻铤底部磁场取向上为正方形;L为无磁钻铤的长度,m;LBit为无磁钻铤底部距离钻头的距离,m),导致更大的方位角误差。为此,选择4种典型的井底钻具组合(见表2),研究了钻具磁干扰对方位角测量的影响(仍取天津地区地磁数据,添加不同钻具组合磁干扰来观测方位角的变化),固定井斜角为90°,结果如图10所示。表 2 4种典型井底钻具组合对比Table 2. Comparison of four typical BHAs底部钻具组合 上部磁极强度/
μWb下部磁极强度/
μWb无磁钻铤距钻头的距离/m 钻头和稳定器 900 90 2 钻头和钻铤 900 300 10 钻头和螺杆钻具 900 1 000 10 钻头和旋转导向 900 3 000 10 由图10可知,底部钻具组合对方位角误差的影响巨大,尤其是螺杆钻具和旋转导向钻具自身所带磁性较大,会产生很大的干扰场。因此,实际应用时要选择合适的底部钻具组合,以更好地消除误差。
3. 方位角误差的修正
测定井眼轨迹过程中,采用磁力随钻测斜仪来测定井斜角、方位角等数据。但钻柱磁化所产生的轴向磁干扰,会影响内部磁通门传感器对地磁场的检测数据。为有效降低干扰磁场的影响,通常采用增加无磁钻铤长度的方法,以增大传感器与铁磁钻具端部的距离,从而减小铁磁钻具端部磁场在传感器位置的干扰磁场,但使用过长的无磁钻铤会增加钻井成本。使用轴向磁干扰的校正算法,也能修正方位角误差,但在井斜角或方位角过大时计算结果并不准确。为了得到更准确的方位角误差和更通用的方位角误差修正方法,笔者提出了基于有限元模拟的方位角误差修正方法,通过模拟计算出方位角误差,消去误差,得到准确的方位角。
3.1 用无磁钻铤减小方位角误差
为降低铁磁钻具对随钻磁力测斜仪的干扰,通常将随钻磁力测斜仪置于无磁钻铤中。无磁钻铤的优点是,可省去后续误差修正过程中繁琐的迭代计算。使用无磁钻铤时应合理选择其长度,过短时随钻磁力测斜仪无法避开钻具磁干扰的影响,过长时由于无磁材料价格昂贵会导致钻井成本升高。
为了研究无磁钻铤长度对磁方位角误差的影响,进行了如下试验:将无磁钻铤长度从3 m依次递增至30 m,钻杆总长度和其他外部条件不变,测量其方位角误差。
试验结果表明,无磁钻铤可为磁力随钻测斜仪提供一个无磁环境,从根本上减小钻具磁化所产生干扰磁场导致的方位角测量误差;随着无磁钻铤长度增加,磁方位角误差逐渐减小。但增加无磁钻铤长度,只能减小方位角误差,无法从根本上消除钻具磁干扰对随钻磁力测斜仪的影响;而且,考虑成本因素,无磁钻铤不能太长。
3.2 轴向磁干扰校正
轴向磁干扰校正的前提是,磁力随钻测斜仪径向磁通门传感器测得的地磁场磁感应强度分量BX和BY是准确的,而影响仪器的干扰磁场沿钻具轴线方向。无磁钻铤前后的钻铤或钻杆不仅沿轴线对称,而且相对钻具轴线上的磁力随钻测斜仪测点较远,故其造成的干扰磁场为钻具轴线方向。比较常用的轴向磁干扰校正方法是短箍校正法,地磁场分量之间的关系如图11所示(图11中:BX'为 BX 在井底圆平面上高边方向的分量,μT; BY'为 BY 在井底圆平面上在侧边(高边方向在井底圆平面上顺时针旋转90°)上的分量,μT; BX''为 BX'在水平面上的分量,μT)。
短箍校正法校正轴向磁干扰的基本原理是:在没有磁干扰的情况下,井斜角、方位角可以通过3个重力加速度分量和3个磁感应强度分量之间的关系计算得到,也可以利用这种关系来反求轴向磁感应强度分量BZc
,然后再利用计算得到的BZc求解方位角。其基本计算公式为: BH=Bcosβ (7) BV=Bsinβ (8) BZc=BHcosφsinα+BVcosα (9) sinφcosφ=−(BXsinϕ+BYcosϕ)cosα(BXcosϕ−BYsinϕ)+BZcsinα (10) 式中:
BH 为地磁场的水平分量,μT ;BV为地磁场的垂向分量,μT ;β 为磁倾角,(°);BZc为磁感应强度轴向分量,μT 。当存在轴向磁干扰时,式(9)和式(10)计算的BZc和
φ 都不准确,需要迭代求解。设置精度值ε,如果当前求解出来的φi+1与上次循环得出的φi相差小于ε,则循环结束;如果大于ε,继续进行循环求解。具体求解过程如图12所示。以井斜角为90°时旋转导向钻具的方位角测量数据为例,把ANSYS Maxwell模拟出来的三轴磁场强度和计算得到的方位角代入轴向磁干扰校正程序,对BZc进行迭代修正,得到修正后的方位角和误差,如图13所示。
从图13可以看出,轴向磁干扰校正可以减小磁干扰引起的方位角误差;但在方位角接近90°和270°(井眼方位朝向正西和正东)时,修正效果并不是特别明显。分析认为,方位角接近正东或正西向时,BZc的值很小,总磁场强度B的小误差就会对BZc校正值产生很大的影响。
轴向磁干扰校正时,结合地磁场和磁力计传感器的各轴读数,采用循环迭代算法消除磁干扰磁场在钻柱轴线上的分量。但这种方法比较依赖地磁场测量的精度,当钻杆轴向磁场很小(钻杆在东西向)时,地磁场很小的误差就会对轴向磁场的计算产生非常大的影响。某些情况下,校正后的结果比原始度数偏离更大,因此不建议在非非区,即在东/西20°(磁性)范围内、井斜角超过70°的区域采用这种方法。
3.3 基于有限元分析的方位角误差修正
综合上述分析,通过导出钻具内部传感器位置处的三轴磁通量计算得到测量方位角,并与模型真实方位角进行比较,就可得出此时的方位角误差。这种方法可以准确控制误差因素的变化,来得到更准确的方位角误差。具体建模步骤如图14所示。
4. 结论与建议
1)随着井斜角增大,方位角误差也逐渐变大,在井斜角等于90°(为水平井)时方位角误差最大。方位角误差在井眼方向为南北时较小,随着井眼方向逐渐靠近东西向,方位角误差也逐渐变大。高纬度地区具有较大的磁倾角,磁场与钻杆始终保持较大的夹角,并且随着纬度增大,磁倾角变化越来越快,对方位角的影响也会越来越大。
2)底部钻具组合具有较大的磁性,会产生很大的干扰场。尤其是螺杆钻具和旋转导向工具,准确选择钻具组合的类型,才能计算出准确的方位角误差。针对旋转导向等磁性较大的工具,直接计算或校正会产生较大误差,采用有限元模拟计算可以得到比较准确的方位角误差参考值和无磁钻铤长度推荐值。
3)采用有限元分析方法时,可以控制干扰源,独立地研究钻具在不同干扰源情况下时方位角误差的变化情况。可以参考有限元分析结果,来解决工程应用时的方位角误差和轴向磁干扰等问题。
4)在总磁场变化不大的情况下,方位角、井斜角和经纬度的变化最终还是体现在钻杆和磁场的夹角变化上。在水平井、东西向井或者高纬度地区,可适当增大无磁钻铤长度来减小方位角误差,之后再通过SCC短箍校正等轴向磁干扰校正方法来减小方位角误差,以保证方位角测量的准确性。
-
表 1 方位角误差模型采用的钻具数据
Table 1 Data of drill tools used in the azimuth error model
钻具或仪器 长度/mm 外径/mm PDC钻头 280 215.9 旋转导向工具 7 520 171.4 BCPM测井工具 4 940 171.4 集成井下测量仪 6 660 171.4 无磁钻铤 9 270 171.4 浮阀 680 165.1 加重钻杆 9 410 127.0 钻杆 9 410 127.0 表 2 4种典型井底钻具组合对比
Table 2 Comparison of four typical BHAs
底部钻具组合 上部磁极强度/
μWb下部磁极强度/
μWb无磁钻铤距钻头的距离/m 钻头和稳定器 900 90 2 钻头和钻铤 900 300 10 钻头和螺杆钻具 900 1 000 10 钻头和旋转导向 900 3 000 10 -
[1] 詹世玉,吴银成,薛宏珍,等. 随钻测量磁干扰消除的研究[J]. 自动化与仪器仪表,2012(5):21–22. doi: 10.3969/j.issn.1001-9227.2012.05.010 ZHAN Shiyu, WU Yincheng, XUE Hongzhen, et al. Research on the magnetic interference elimination of MWD[J]. Automation & Instrumentation, 2012(5): 21–22. doi: 10.3969/j.issn.1001-9227.2012.05.010
[2] 毛建华,王清江. MWD磁干扰的分析判断方法探讨[J]. 钻采工艺,2008,31(3):129–130. doi: 10.3969/j.issn.1006-768X.2008.03.042 MAO Jianhua, WANG Qingjiang. Discussion on analysis and judgment method of MWD magnetic interference[J]. Drilling & Production Technology, 2008, 31(3): 129–130. doi: 10.3969/j.issn.1006-768X.2008.03.042
[3] 宋晓健,董晨曦. 磁性测斜工具中关于方位角校正的研究[J]. 石化技术,2015,22(9):181. doi: 10.3969/j.issn.1006-0235.2015.09.137 SONG Xiaojian, DONG Chenxi. Study on the correction of azimuth angle in magnetic measurement[J]. Petrochemical Industry Technology, 2015, 22(9): 181. doi: 10.3969/j.issn.1006-0235.2015.09.137
[4] 王小龙. 铁磁钻具引起测斜仪方位角误差的校正方法研究[J]. 地球物理学进展,2019,34(6):2521–2525. doi: 10.6038/pg2019CC0518 WANG Xiaolong. Nearly horizontal drill hole attitude measurement and aizmuth error correction caused by drilling tool[J]. Progress in Geophysics, 2019, 34(6): 2521–2525. doi: 10.6038/pg2019CC0518
[5] WILLIAMSON H S. Accuracy prediction for directional measurement while drilling[J]. SPE Drilling & Completion, 2000, 15(4): 221–233.
[6] 张苏,管志川,王建云,等. 邻井套管对井斜方位角的影响[J]. 石油钻探技术,2013,41(6):51–55. doi: 10.3969/j.issn.1001-0890.2013.06.010 ZHANG Su, GUAN Zhichuan, WANG Jianyun, et al. Impact of casing on adjacent well azimuth[J]. Petroleum Drilling Techniques, 2013, 41(6): 51–55. doi: 10.3969/j.issn.1001-0890.2013.06.010
[7] GRINDROD S J, WOLFF J M. Calculation of NMDC length required for various latitudes developed from field measurements of drill string magnetisation[R]. SPE 11382, 1983.
[8] 狄勤丰,芮子翔,周星,等. 带旋转导向工具的底部钻具组合横向振动特性研究[J]. 石油钻探技术,2021,49(6):8–16. doi: 10.11911/syztjs.2021059 DI Qinfeng, RUI Zixiang, ZHOU Xing, et al. Research on lateral vibration characteristics of bottom hole assembly with rotary steerable tool[J]. Petroleum Drilling Techniques, 2021, 49(6): 8–16. doi: 10.11911/syztjs.2021059
[9] 刘修善. 井眼轨迹精准定位技术[J]. 石油钻探技术,2017,45(5):8–12. LIU Xiushan. Precise positioning technique for wellbore trajectories[J]. Petroleum Drilling Techniques, 2017, 45(5): 8–12.
[10] 刘修善. 定向钻井轨道设计与轨迹计算的关键问题解析[J]. 石油钻探技术,2011,39(5):1–7. doi: 10.3969/j.issn.1001-0890.2011.05.001 LIU Xiushan. Analysis of the key issues involved in wellpath planning and trajectory calculation for directional drilling[J]. Petroleum Drilling Techniques, 2011, 39(5): 1–7. doi: 10.3969/j.issn.1001-0890.2011.05.001
[11] 王明哲,陆斌,于跃军. Sperry-Sun MWD轴向磁干扰的解决方法及应用[J]. 石油仪器,2008,22(2):47–49. WANG Mingzhe, LU Bin, YU Yuejun. Solution to the axial magnetic interference on Sperry-Sun MWD[J]. Petroleum Instruments, 2008, 22(2): 47–49.
[12] 许昊东,黄根炉,张然,等. 磁力随钻测量磁干扰校正方法研究[J]. 石油钻探技术,2014,42(2):102–106. XU Haodong, HUANG Genlu, ZHANG Ran, et al. Method of magnetic interference correction in survey with magnetic MWD[J]. Petroleum Drilling Techniques, 2014, 42(2): 102–106.
[13] 范光第,蒲文学,赵国山,等. 磁力随钻测斜仪轴向磁干扰校正方法[J]. 石油钻探技术,2017,45(4):121–126. FAN Guangdi, PU Wenxue, ZHAO Guoshan, et al. Correction methods for axial magnetic interference of the magnetic inclinometer while drilling[J]. Petroleum Drilling Techniques, 2017, 45(4): 121–126.
[14] 孟卓然. BHA轴向磁干扰对方位测量误差的影响: 基于人工磁场模拟方法[J]. 石油学报,2020,41(8):1011–1018. doi: 10.7623/syxb202008010 MENG Zhuoran. Effect of BHA axial magnetic interference on the azimuth measurement error: a simulation method based on artificial magnetic field[J]. Acta Petrolei Sinica, 2020, 41(8): 1011–1018. doi: 10.7623/syxb202008010
[15] 刘修善,王继平. 基于大地测量理论的井眼轨迹监测方法[J]. 石油钻探技术,2007,35(4):1–5. doi: 10.3969/j.issn.1001-0890.2007.04.001 LIU Xiushan, WANG Jiping. A method for monitoring wellbore trajectory based on the theory of geodesy[J]. Petroleum Drilling Techniques, 2007, 35(4): 1–5. doi: 10.3969/j.issn.1001-0890.2007.04.001
[16] 范光第,隋海东,黄根炉,等. 基于ANSYS的邻井套管磁干扰有限元仿真[J]. 石油机械,2013,41(8):1–4. doi: 10.3969/j.issn.1001-4578.2013.08.001 FAN Guangdi, SUI Haidong, HUANG Genlu, et al. ANSYS-based finite element simulation of magnetic disturbance of casing in adjacent well[J]. China Petroleum Machinery, 2013, 41(8): 1–4. doi: 10.3969/j.issn.1001-4578.2013.08.001
[17] FINLAY C C, MAUS S, BEGGAN C D, et al. International geomagnetic reference field: the eleventh generation[J]. Geophysical Journal International, 2010, 183(3): 1216–1230. doi: 10.1111/j.1365-246X.2010.04804.x
-
期刊类型引用(7)
1. 张纯,孙山,韩煜航. 参数耦合下风力发电机叶片机械颤振检测研究. 自动化与仪表. 2024(01): 102-106 .  百度学术
百度学术
2. 魏琦. 大口径管道水平定向钻穿越大型河流施工风险控制研究. 铁道建筑技术. 2024(03): 188-192 .  百度学术
百度学术
3. 刁斌斌,高德利,刘喆,吴华鹏. 井深随钻测量误差校正与井眼位置不确定性计算方法. 石油钻探技术. 2024(02): 181-186 .  本站查看
本站查看
4. 花谊昌,龙远,王学迎,王越之,荣淮. 硬地层防斜打快底部钻具组合结构优化研究. 天然气与石油. 2024(03): 110-116 .  百度学术
百度学术
5. 孙龙飞,王晓鹏,张启龙,谢涛,林海,董平华,尚捷. 旋转导向近钻头方位伽马测量仪研制与应用. 石油工业技术监督. 2023(11): 51-54 .  百度学术
百度学术
6. 于瑞丰,刁斌斌,高德利. 考虑磁方位校正的井眼轨迹测量误差计算. 石油钻探技术. 2023(06): 25-31 .  本站查看
本站查看
7. 蒲文学,范光第,朱建建,赵国山. 磁性随钻测斜仪所需无磁钻具长度及影响因素研究. 石油钻探技术. 2022(04): 129-134 .  本站查看
本站查看
其他类型引用(0)




 下载:
下载: