长水平段水平井钻井过程中，钻进、循环、划眼和倒划眼等工况交替进行，井下岩屑床在轴向上呈不均匀分布。研究水平井岩屑床轴向运移规律，有利于分析岩屑床在井下的轴向分布，进一步分析易卡钻点、井筒压力分布和机械延伸极限等问题^[1–5]。前人基于室内试验和数值模拟方法，考虑转速、岩屑粒径、钻井液性能等因素，研究了水平井岩屑运移规律，分析了井筒截面上岩屑床高度的变化^[6–9]。另外，国内外学者利用机理建模的方法，研究了岩屑床在井筒轴向的分布，这些模型通常采用试验中岩屑床高度或井筒压降来验证模型，却没有试验结果支撑模型计算的岩屑床在井筒轴向上的运移规律^[10–11]。现场实践中，采用立管压力和机理模型相结合的方式，用ECD来反演井眼清洁程度^[12]，但只有立管压力一个实测数据，无法准确反映岩屑床在井筒中的轴向分布。Zhang Feifei等人^[13]提出了利用沿管柱环空压力（ASAP）评价大位移井岩屑床轴向分布的方法，该方法通过多个压力传感器实时测量沿管柱环空压力，利用井筒轴向各段井筒压降与岩屑浓度的映射关系，实现了井下岩屑床轴向分布的预测。M. M. Huque等人^[14–15]利用电阻层析成像（electrical resistance tomography，ERT）技术，进行了岩屑床在井筒中轴向位置随时间变化的试验研究，分析了不同流速、井斜角等条件下岩屑床的运移速度，但进行井下作业时无法应用ERT技术。此外，虽然利用ASAP评价井眼清洁的技术具有潜在应用价值，但缺乏试验和理论支撑。

为了探索旋转钻进工况下水平井岩屑床的轴向运移规律，笔者设计了沿井筒轴向布置多个压差传感器的井筒多相流动室内试验系统，提出了基于多点实时测量压降的方式研究岩屑床轴向运移规律的方法，在清水、盐水中开展了水平井岩屑运移试验，分析了排量和转速对水平井岩屑床轴向运移的影响规律，为优选安全高效钻进的激进工程参数（大钻压、高转速、大排量）提供了试验和理论依据。

1.   井筒多相流动室内试验系统

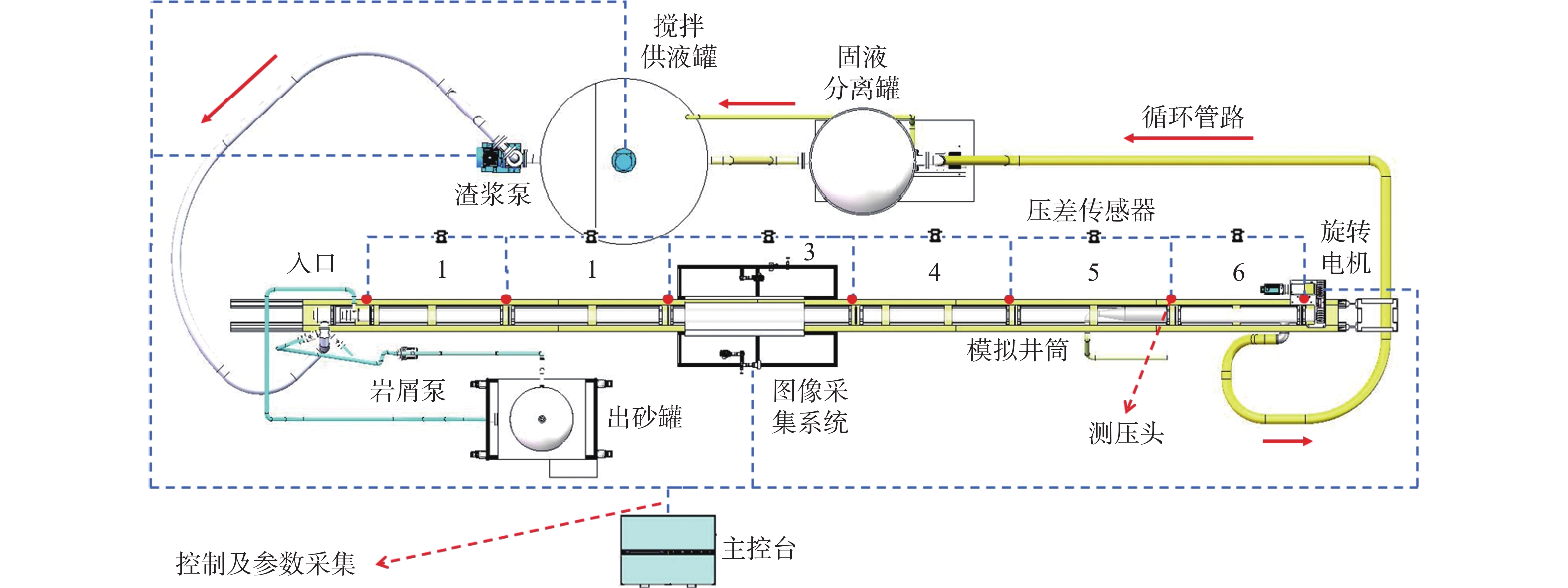
为研究高速钻进时水平段井筒中的岩屑运移规律，研制了模拟高钻速、大排量和高转速的井筒多相流动室内试验系统（见图1）。该系统以长12 m的透明井筒为试验管路，配备可电控调节参数的偏心旋转钻杆、供液和供岩屑系统等，其中透明井筒外径180 mm、内径138 mm，钻杆外径78 mm，偏心度0.85。井筒上每隔2 m安装有压差传感器，可实时采集6个压差传感器的压降，并实时导出不同排量、转速下的井筒压降，为分析岩屑床的轴向分布和计算岩屑床运移速度提供基础。根据井筒多相流动理论，一般认为井筒的长径比（长度/水力直径）在50以上，可满足管流充分发展的要求^[8]，该井筒长径比为200，满足流动充分发展的要求。通过出砂罐下方的控制器，使井筒保持一定的进砂速率，根据标定的进砂速率及试验井筒尺寸，计算模拟的机械钻速。

图  1  井筒多相流动试验系统示意

Figure  1.  Experimental system for multiphase flow in the wellbore

下载: 全尺寸图片 幻灯片

2.   基于压差法的水平井岩屑运移试验

为明确水平井岩屑床轴向运移规律，设计了高钻速、大排量和高转速的试验参数，提出了岩屑床轴向运移测量方法，给出了试验步骤。

2.1   试验参数

试验设置机械钻速为18.6 m/h，排量分别为18，24，32，40，48和56 m³/h，转速分别为0，50，100，150和200 r/min。试验岩屑为密度2 596 kg/m³的不规则石英砂，粒径1，2，3和4 mm岩屑的质量分数分别为13.11%，42.74%，41.90%和2.25%，分别在清水和密度为1.16 g/cm³的盐水中进行试验。

2.2   岩屑床轴向运移测量方法

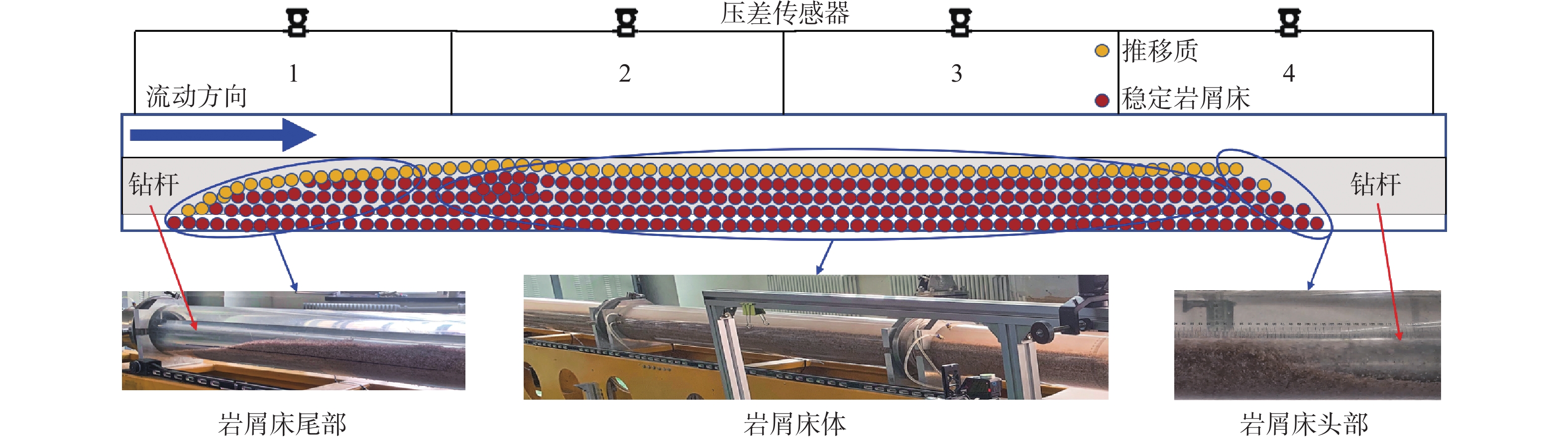
为了很好地研究岩屑床轴向运移规律，提出了通过在井筒上依次排布压差传感器来计算岩屑床运移速度的方法。在12 m长的井筒上，每隔2 m布置1个压差传感器（见图1），每个压差传感器两端连接管线，管线终端的测压头分别连接井筒，测压头间距为2 m，依次标定为压差传感器1，2，…，6，并每隔2 s采集1次井筒压降，通过软件将数据传输至计算机。该方法可以针对井筒不同轴向区域采集压降数据。现场应用时可在二开、三开完井段布置传感器，或者采用沿管柱布置传感器的方法^[13]，测量井下压降并分析岩屑床的堆积情况，预估钻进段的井筒压力，从而规避敏感地层可能发生的井涌、井漏和卡钻等风险。

试验时，随着岩屑持续注入，岩屑床逐渐堆积形成。由于岩屑在入口处是抛物线运动，井筒入口端会出现一段无岩屑床的空间，该段的长度在不同试验条件下会发生改变（见图2），在本文试验参数下均位于压差传感器1测量的2 m内，称为岩屑床尾部。在相同试验条件下岩屑床保持稳定运移时，由于持续注入岩屑，岩屑床尾部保持不动，处于动态平衡状态。随着岩屑堆积，岩屑床体高度先小幅度升高，然后保持稳定，该段称为岩屑床体，本文研究提出的岩屑床运移速度即为岩屑床体的形成速度。在岩屑堆积前端即岩屑床头部，岩屑床高度逐渐降低。需要说明的是，本文研究的岩屑床运移速度并不是岩屑床头部最前端的运移速度，而是岩屑床头部达到稳定高度时（即岩屑床体前端）的运移速度。在试验中，考虑井筒的端部效应，岩屑床体铺置满传感器3测量的位置，距离入口端4～6 m，岩屑床头部已运移至传感器4测量的6～8 m内。根据计算，距入口端4～6 m满足流动充分发展的要求，长径比为66.7～100.0。

图  2  钻进工况岩屑床轮廓

Figure  2.  Cuttings bed profile under drilling conditions

下载: 全尺寸图片 幻灯片

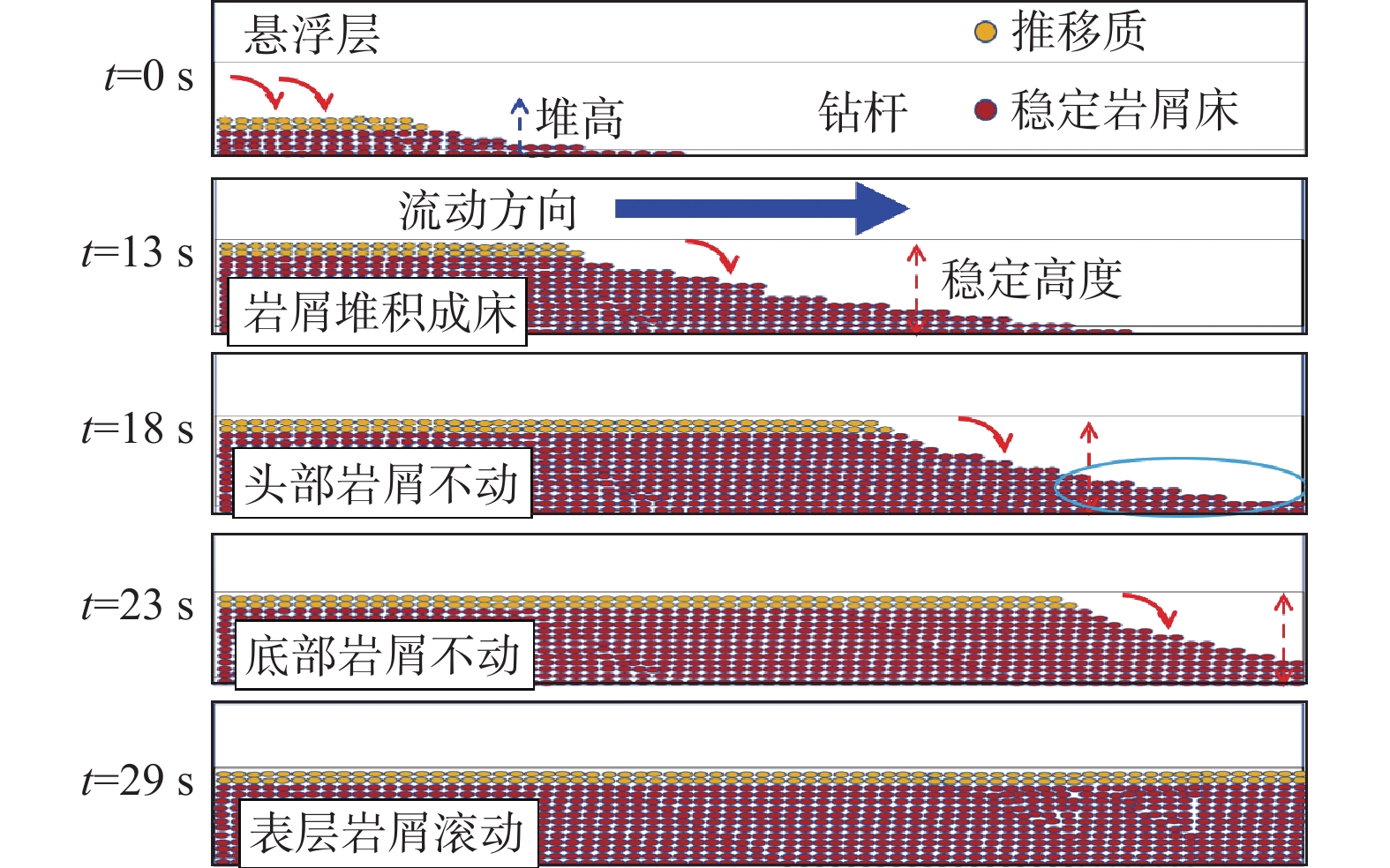
传感器3测量段（距离井筒入口端4～6 m）岩屑床头部的铺置情况如图3所示。该图为拍摄视频的示意图，视频中井筒长度为0.75 m。在岩屑床头部进入录制区（t=0～13 s）时，岩屑床体表层岩屑滚动至该区域，沉降堆高岩屑床至稳定高度。岩屑床头部最前端岩屑未堆积到稳定高度，该处岩屑不动；随着时间推进，流体冲蚀岩屑床体表层岩屑，逐渐将岩屑床头部堆高。表层滚动岩屑之下岩屑床的高度保持稳定，岩屑床体逐渐变长。

图  3  岩屑床头部铺置流型随时间变化情况

Figure  3.  Time-dependent deposition patterns at the head of the cuttings bed

下载: 全尺寸图片 幻灯片

压差传感器的测量结果如图4所示。测量值1—5分别为压差传感器1—5每间隔2 s的测量数据。由测量值1可知，随着时间发展，传感器1所测位置压降逐渐升高并达到一个稳定值，传感器1压降达到稳定值说明该处已形成高度稳定的岩屑床，该结果与可视化试验观察结果一致。随着时间推进，测量值2也将达到稳定状态，此刻（t=144 s）说明传感器1和2所测0～4 m段的岩屑床达到稳定状态，同理传感器3压降数据保持稳定时(t=190 s)，距岩屑入口端井筒0～6 m处的岩屑床也达到稳定状态。在2～4 m和4～6 m形成稳定岩屑床所需时间较为相近，说明岩屑床运移速度已达到稳定，运移速度基本不变，但为了测量流动充分发展情况下岩屑床的运移速度，以距离入口端4～6 m岩屑床的运移为研究对象。

图  4  岩屑床轴向动态运移不同位置传感器测得压降

Figure  4.  Pressure drop data from sensors at different positions during axial dynamic transport of the cuttings bed

下载: 全尺寸图片 幻灯片

式中：v_bed为岩屑床移动速度，m/s；${\Delta }{x}$_bed为高度稳定岩屑床的运移距离，m；Δt₂为岩屑床运移某段距离所需的时间，s。

另外，岩屑床运移至传感器测量段初期会导致井筒压降先降低再升高。研究表明，随着岩屑床堆积悬浮层截面积减小，悬浮层流速升高和岩屑床表面粗糙导致摩擦压降增大，但在传感器一端刚形成岩屑床而另一端仍为单相流动时，流动速度相差较大。根据伯努利原理，等高流动时，流速越大压力越小，因此会出现压降降低的情况。

式中：p_p为流体中某点压强，Pa；v_p为流体某点流速，m/s；ρ为流体密度，kg/m³；g为重力加速度，m/s²；h_p为该点所在高度，m。

由于存在端部效应，传感器1距离入口近的测量点处并未形成岩屑床，因此测量值1并未出现前期压降降低的情况，传感器2—5均出现该现象。

2.3   试验步骤

1）循环试验流体直至井筒内无气泡，保持稳定排量循环单相流体，开启压差传感器采集压降数据；2）保持一定速率持续注入岩屑，开启电机钻杆保持旋转，压差传感器持续采集两相岩屑运移条件下的井筒压降数据；3）当稳定岩屑床运移至传感器3处（距离入口端4～6 m），拍摄视频；4）当稳定岩屑床运移至压差传感器4处（距离入口端6～8 m）时停止试验，保存井筒压降数据；5）回收岩屑，改变试验条件，重复以上试验步骤。

3.   岩屑床轴向运移规律分析

3.1   压降结果验证

采集清水在井筒环空内循环时的压降数据，利用文献[16]中的环空压降计算模型计算不同排量（8.08～72.89 m³/h）下井筒环空的压降。文献[16]的环空压降计算模型为：

式中：F_f为环空内流体单位长度上的摩擦压降，Pa/m；f为范宁摩擦因子；v为环空流体流速，m/s；D_o为井眼直径，m；D_i为钻杆外径，m。

根据雷诺数范围计算范宁摩擦因子，当雷诺数Re≤2 100（层流）时，范宁摩擦因子的计算公式为：

当雷诺数Re>2 100（湍流）时，范宁摩擦因子的计算公式为：

式中：Re为雷诺数；μ为环空内流体黏度，Pa∙s。

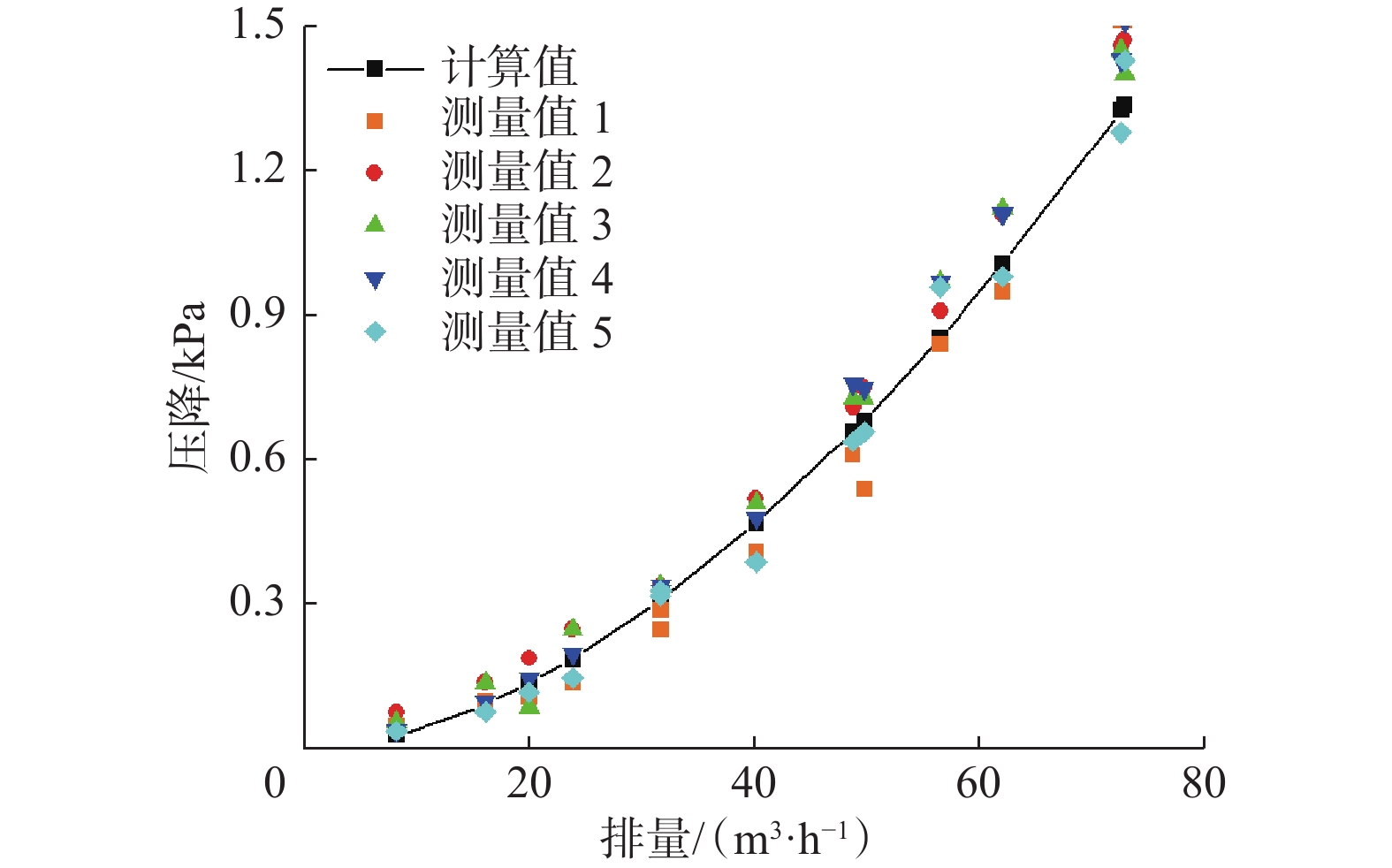
环空压降计算结果与测量数据结果如图5所示，并计算了不同排量下压差传感器测量值与计算结果的相对误差，传感器测量结果的平均相对误差在20%以内，其中传感器2和3的相对误差分别为9.72%和8.74%。从图5可以看出，测量结果与压降模型计算结果的规律一致，后文采集的两相运移压降为传感器3达到稳定岩屑床状态的数值，传感器的测量精度满足试验要求。

图  5  计算与实测的井筒压降

Figure  5.  Calculated and measured wellbore pressure drop

下载: 全尺寸图片 幻灯片

3.2   流体密度对岩屑床运移速度的影响

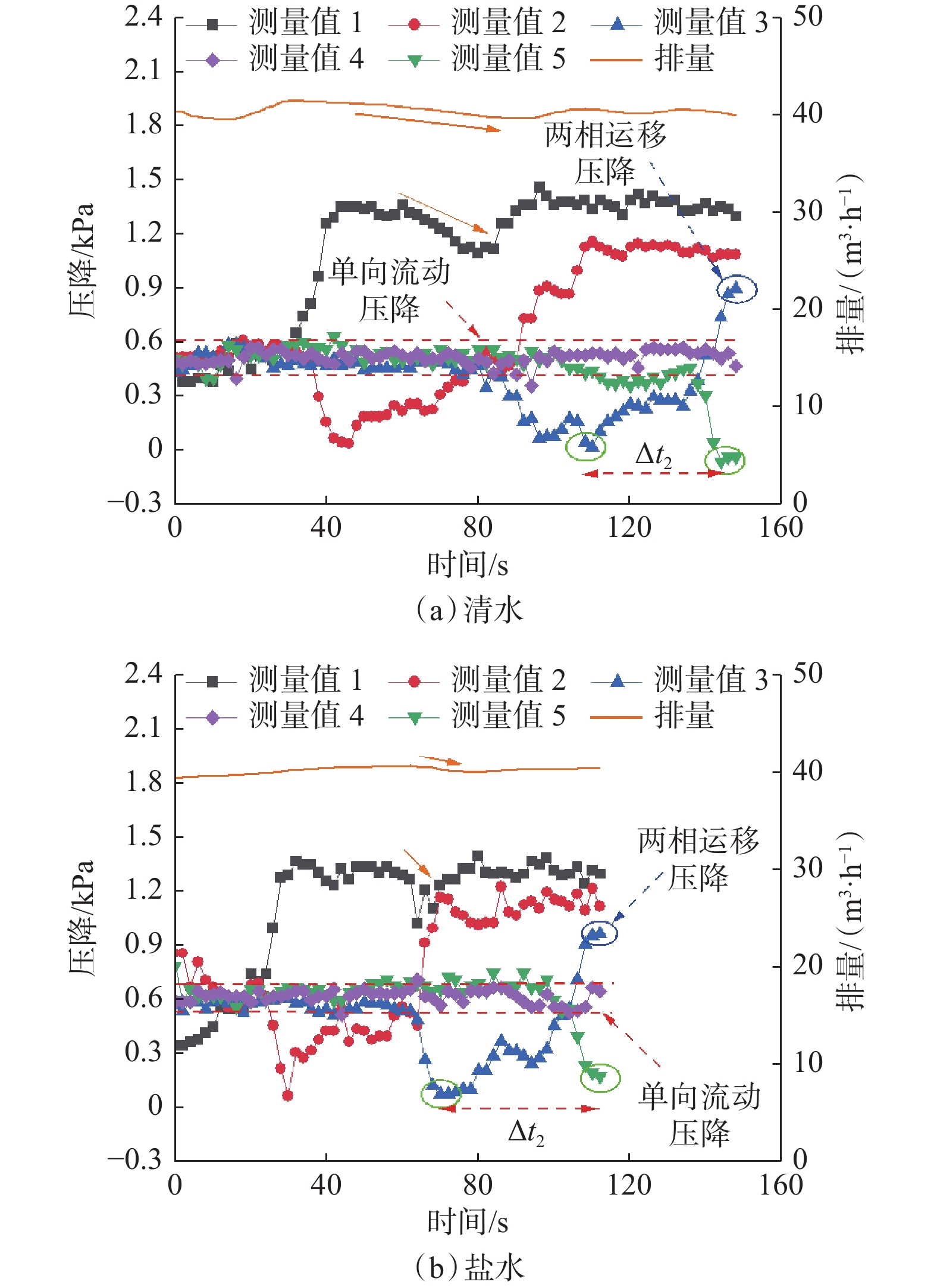
传感器数据可以反映液体单相流动时的压降、固液两相运移时的压降和岩屑床的运移速度。岩屑未进入相应测量井段时，采集的数据为单相流动压降，为保证结果客观，该值为各传感器单相流动时测量时序数据的平均值；形成稳定岩屑床后，井筒压降保持稳定，为两相运移压降，考虑端部效应，采用传感器3的测量数据（见图6）。2组流体的排量均为40 m³/h，环空流速为1.09 m/s，与实际钻井的环空返速较为接近。由图6可知，经过控制器的微调节，排量平均相对波动幅度小于0.90%；排量降低，达到稳定状态时的测量值1小幅降低，说明传感器具有较高的灵敏度，测量结果真实可靠。

图  6  不同流体中各压差传感器的测量值

Figure  6.  Measurement values of differential pressure sensors in different fluids

下载: 全尺寸图片 幻灯片

根据图6（a）和6（b）中标记的单相流动压降和两相运移压降得到图7，利用式（6）计算得到2组试验的雷诺数分别为52 942和61 413，单相流动时为湍流，由式（3）和式（5）可知，湍流条件下高密度流体流动压降较高。由图7可知，流体密度增大，两相运移的环空压降和单相流动的环空压降均升高，但两相运移的环空压降升高幅度更大。根据图6（a）和6（b）中岩屑床体长度增加2 m所需的时间，计算出岩屑床运移速度分别为0.045 m/s和0.048 m/s。分析认为，岩屑在高密度流体中所受的浮力增大，导致沉降速度降低，进而引起岩屑床运移速度增大。

图  7  不同流体中压差传感器井筒压降测量值及岩屑床的运移速度

Figure  7.  Measured values of wellbore pressure drop by differential pressure sensors and cuttings bed transport velocity in different fluids

下载: 全尺寸图片 幻灯片

3.3   排量对岩屑床运移速度的影响

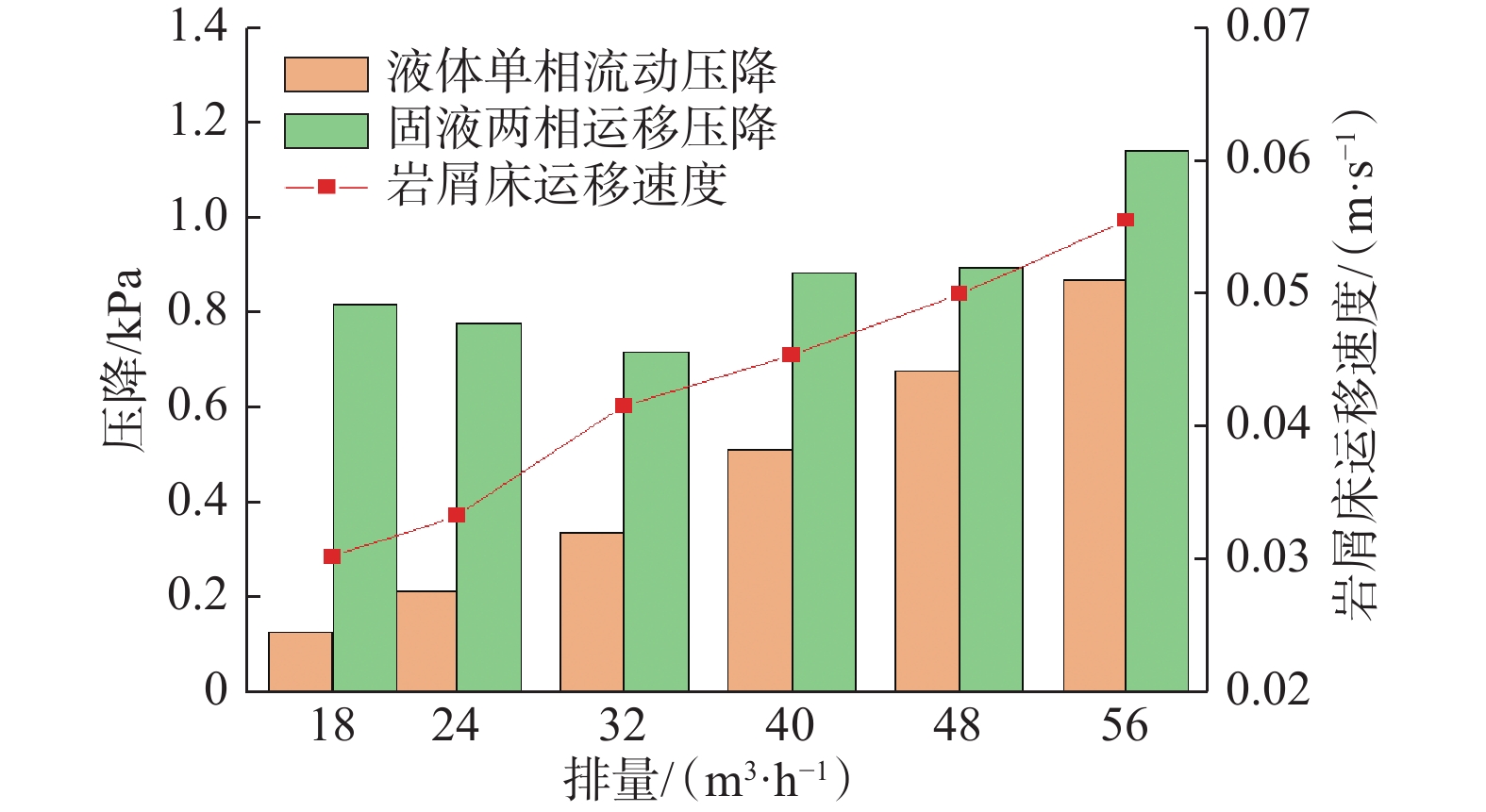
为分析排量对岩屑床运移速度的影响，开展了清水中水平井岩屑运移试验，得到了不同排量下的井筒压降测量值（见图8），雷诺数在23 824.0～74 119.2，均为湍流流动。从图8可以看出，随着排量增大，时间为0点右侧单相流动的压降逐渐增大，与堆积岩屑后井筒压降的差值变小。

图  8  不同排量下各压差传感器的测量值

Figure  8.  Values of differential pressure sensors under different flow rates

下载: 全尺寸图片 幻灯片

根据前文所述计算方法，计算了不同排量下的单相流动压降、固液两相运移压降及岩屑床运移速度（见图9）。从图9可知，排量从18 m³/h增至32 m³/h时，固液两相运移压降降低；排量从32 m³/h增至56 m³/h时，固液两相运移压降升高，岩屑床运移速度从0.030 m/s增至0.056 m/s。以2 000 m长水平井筒为例，排量从40 m³/h增至56 m³/h时，根据岩屑床运移速度计算出每小时堆积岩屑床的长度从163 m增至200 m，假设井筒内岩屑床均达到稳定状态，两相运移压降将升高255 kPa。

图  9  不同排量下压差传感器测得井筒压降及岩屑床运移速度

Figure  9.  Measured wellbore pressure drop by pressure differential sensors and cuttings bed transport velocity under different flow rates

下载: 全尺寸图片 幻灯片

3.4   钻杆转速对岩屑床运移速度的影响

为分析钻杆转速对岩屑床运移速度的影响，采用盐水进行了排量为40 m³/h的水平井岩屑运移试验，钻杆转速分别为50，100，150和200 r/min时的井筒压降测量结果如图10所示。其中，转速50 r/min试验组在测量时钻杆即开始旋转，转速100，150和200 r/min试验组从图10中标定时间开始旋转。由图10（b）（c）（d）可知，当钻杆开始旋转后，测量值1明显开始降低，并且随转速增加下降趋势加快。对比图10（b）（c）（d）中的Δt₁和Δt₂可知，钻杆旋转后Δt₂迅速缩短，即岩屑床运移速度加快。岩屑床在0～6 m达到稳定状态时，随着转速增加，测量值1、2、3的差值减小，说明钻杆旋转有利于井筒压降的均匀分布。

图  10  不同钻杆转速下各压差传感器测量值

Figure  10.  Measured values of differential pressure sensors under different drill pipe rotation speeds

下载: 全尺寸图片 幻灯片

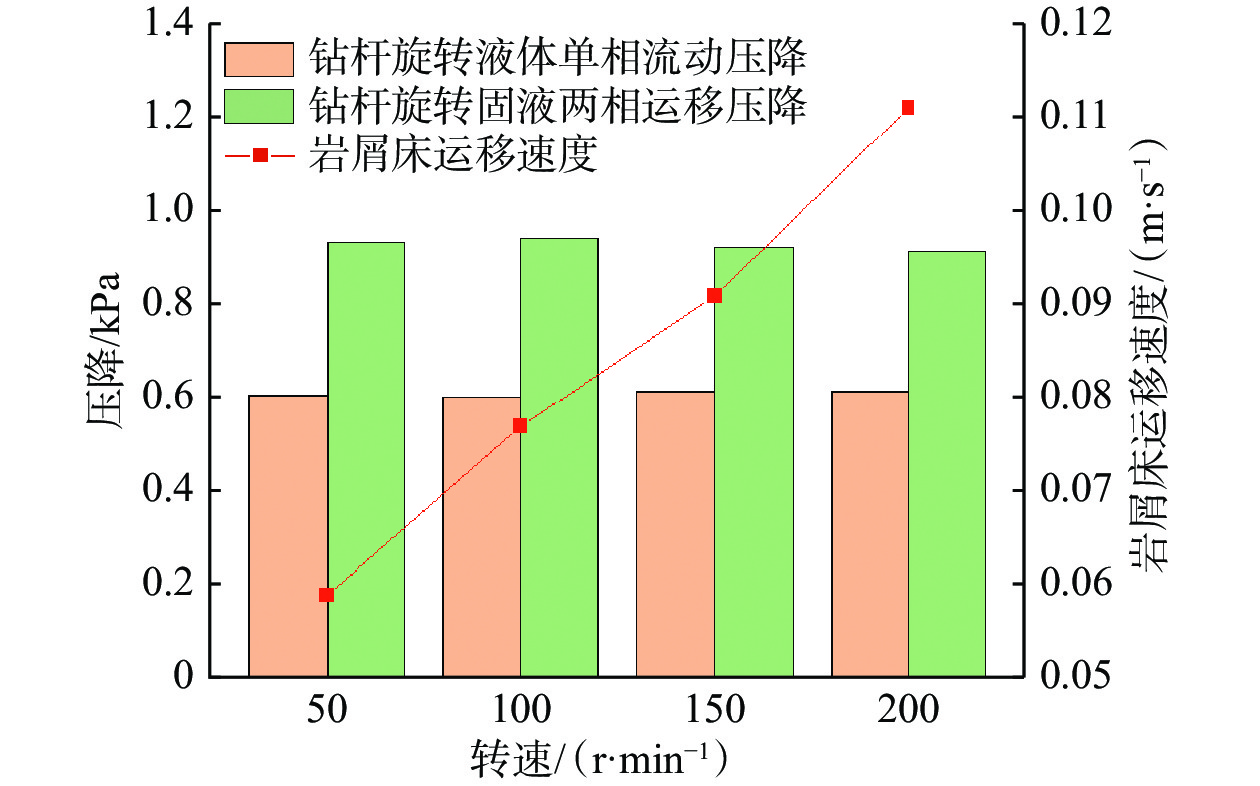
根据上述计算方法，计算得到了不同钻杆转速下的单相流动压降、固液两相运移压降及岩屑床运移速度（见图11）。从图11可以看出，钻杆转速对单相流动压降和固液两相运移压降影响较小（平均值分别为0.609和0.927 kPa，方差分别为3.075×10⁻⁵和1.111×10⁻⁴），但对岩屑床运移速度的影响极大；钻杆转速从50 r/min提高至200 r/min，岩屑床运移速度提高了88.9%；根据岩屑床运移速度计算出每小时堆积岩屑床的长度将从212 m增加至400 m，极大地提高了岩屑清除效率。

图  11  不同钻杆转速下压差传感器井筒压降测量值及岩屑床的运移速度

Figure  11.  Measured values of wellbore pressure drop by pressure differential sensors and cuttings bed transport velocity under different drill pipe rotation speeds

下载: 全尺寸图片 幻灯片

以上研究表明，流体密度、排量和钻杆转速增大，使岩屑床运移速度加快，流体密度和排量增大均对井筒压降的影响较大，但钻杆转速增大对井筒压降的影响较小。

4.   结论及建议

1）在水平井旋转钻进工况下，岩屑运移呈岩屑床推进，悬浮层几乎无岩屑。在一定的排量和转速下，岩屑床头部铺置至稳态高度后，才继续轴向铺置岩屑床，且铺置速度一定。利用压差法计算了岩屑床运移速度，揭示了岩屑床在井筒轴向的运移规律，为现场测定井下岩屑床的轴向分布提供了试验和理论依据。

2）岩屑床运移速度随流体密度、排量和钻杆转速增大而加快，提高排量和钻杆转速可以使井筒中岩屑床长度成倍增加。随流体密度升高固液两相运移压降增大，随排量增大两相运移压降存在拐点，钻杆转速对两相运移压降的影响较小。

3）在不同排量和转速下进行试验时，未考虑高黏度非牛顿流体、钻杆晃动和井筒不规则等情况，且未考虑不同偏心度的影响，存在一定局限性。建议针对上述问题，进一步探索岩屑床轴向运移规律。

4）排量和钻杆转速对岩屑床运移速度的影响较大，但排量增大会导致井筒压降增大，然而钻杆转速却对井筒压降几乎无影响。在高钻速的激进钻进参数下，针对压力敏感地层，提高钻杆转速更有利于提高岩屑清除效率。