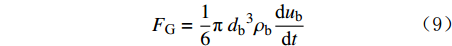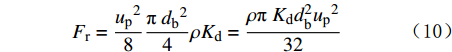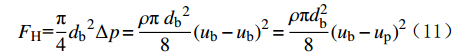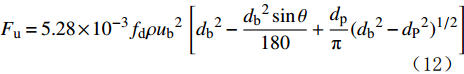Numerical Simulation Study on the Migration Characteristics of Ball Sealers in Horizontal Shale Gas Wells
-
摘要:
水平井暂堵压裂技术是提高非常规储层改造效果的关键，而暂堵球在水平井中的运移及封堵特性的准确预判是水平井暂堵压裂成功实施的关键。因此，需要利用数值模拟方法模拟暂堵球在水平井的运移和封堵特性。由于CFD-DEM耦合模型能够将暂堵球颗粒视为旋转的球体，实现颗粒与流体之间的双向耦合，因此基于CFD-DEM耦合方法建立了页岩气水平井井筒暂堵模型，分析了暂堵球粒径、压裂泵注排量和暂堵球密度对暂堵球运移和封堵性能的影响，结果表明，对于ϕ139.7 mm的单簇8孔螺旋分布式套管，孔眼与暂堵球直径之比为0.97左右时井筒暂堵效果最好；暂堵球的坐封效率随着泵注排量增大呈先升高后降低的趋势，泵注排量低于6 m3/min时，随着泵注排量增大，暂堵球坐封效率升高；泵排量为4～7 m3/min时，暂堵球的坐封效率较高；低密度暂堵球的坐封效率最高，高密度暂堵球的坐封效率最低；暂堵球最容易坐封在射孔簇后半段孔眼上，也能够坐封在第1个孔眼上。研究结果表明，基于CFD-DEM耦合的页岩气水平井井筒暂堵模型能够实现暂堵球在水平段运移过程的可视化，利用其可预测暂堵球的运移速度及坐封孔眼的位置，为水平井暂堵压裂施工设计提供指导。
Abstract:Temporary plugging fracturing of horizontal wells is the key to improving the stimulation results of unconventional reservoirs. The accurate prediction of the migration and plugging characteristics of the ball sealer in horizontal wells plays a prominent role in the successful implementation of the temporary plugging and fracturing of horizontal wells. Therefore, it is necessary to employ numerical simulation methods to simulate the migration and plugging characteristics of ball sealer in horizontal wells. Since the coupled CFD-DEM model can treat the ball sealer as a rotating sphere and accomplish two-way coupling between particle and fluid, a numerical model of wellbore temporary plugging in horizontal shale gas wells was established based on the CFD-DEM coupling method to analyze the influence of ball sealer diameter, fracturing pump rate, and ball sealer density on the migration and sealing behavior of ball sealers. The results showed that for a casing diameter of ϕ139.7 mm, with a single-cluster and a 8-perforation spiral distribution, the effect of wellbore temporary plugging was the best when the ratio of perforation diameter to ball sealer diameter was about 0.97. The sealing efficiency of the ball sealer first increased and then decreased with the increase of pump rate. When the pump rate was less than 6 m3/min, the sealing efficiency of the ball sealer increased with the increase in the pump rate. When the pump rate was 4–7 m3/min, the sealing efficiency of the ball sealer was higher. The low-density ball sealer had the highest sealing efficiency, and the high-density ball sealer had the lowest sealing efficiency. In addition, the ball sealer was most likely to seal the perforation in the second half interval of the perforation cluster or the first perforation. The temporary plugging model of horizontal shale gas wells based on CFD-DEM coupling can provide a visualization of the migration process of the ball sealer in the horizontal section and predict the migration speed of the ball sealer and the position of the sealed perforation, which provides a guideline for the temporary plugging fracturing design and field implementation in horizontal wells.
-
Keywords:
- shale gas /
- horizontal well /
- temporary plugging fracturing /
- ball sealer /
- numerical simulation /
- CFD-DEM model
-
我国油气资源开发已经从常规油气转向了页岩、致密砂岩油气等非常规资源，同时基于国家“十四五”发展规划，非常规油气将成为我国油气增储上产的主力。对于非常规油气特别是页岩油气的开发，大规模体积压裂是提高储层改造效果的关键[1-3]。但传统压裂方法成本高、效果差，因此多采用水平井分段多簇压裂技术改造页岩油气储层，实现页岩油气的经济开发[4]。页岩油气储层一般埋藏深、物性差，平面及纵向非均质性强，采用水平井分段压裂技术改造时，由于裂缝间应力相互干扰使多簇裂缝间扩展不均，储层增产改造效果不佳[5]。在此背景下，井筒暂堵压裂技术应运而生，该技术能够有效调控裂缝扩展，从而促使裂缝均衡扩展，有利于提高页岩油气储层的压裂改造效果，许多油田应用该技术改造油气层，并取得了显著成效[6-7]。井筒暂堵是指在非均质性较为严重的储层中投入暂堵球，对优势裂缝孔眼进行暂堵，从而使后续压裂液流向未改造储层，促使劣势裂缝进行扩展，达到分层分段改造、裂缝均衡起裂扩展的目的，从而提高油气产量[8-10]。颗粒类暂堵球是目前封堵裂缝及孔眼常用的材料，其承压能力强，对储层的伤害低，并且在一段时间后能够自行降解，满足施工需求[11]。
页岩储层水平井套管射孔段多簇孔眼螺旋分布，通过压力检测只能粗略判断部分孔眼是否封堵，对暂堵球在水平射孔段运移及坐封规律的研究不足，主要依靠现场经验进行暂堵压裂施工，不能精确预判暂堵球的运移与封堵行为，使投球暂堵后裂缝扩展不均，导致储层改造效果不佳[6]。对于暂堵球在井筒中的运动规律，学者们进行了相关研究，肖辉等人[12]研究发现暂堵球在水平井中的运动主要分为前期的加速运动和后期的匀速运动；蔡华等人[13]发现暂堵球坐封在孔眼上时主要受到来自于射孔压差的持球力和管内流体作用在暂堵球上的脱落力，当持球力大于脱落力时，暂堵球才会坐封在孔眼上；许江文等人[10]通过试验分析了暂堵球形状影响裂缝封堵的规律；刘明明[14]通过研究暂堵球在水平井中的受力得到了暂堵球的运动方程；郑志兵[15]研究了暂堵球的受力情况，以及泵注排量、暂堵球密度、孔眼数量对坐封效率的影响；李春月等人[16]改进了三轴压裂物模试验装置，利用其进行了暂堵转向压裂试验，研究了碳酸盐岩裂缝暂堵转向规律和实现缝内暂堵转向的条件；夏海帮[17]针对页岩气井暂堵后压力升高不明显的问题，优选了暂堵工艺，优化了暂堵参数，形成了页岩气井双暂堵压裂技术，南山页岩气田应用后取得了显著效果；周丹等人[18]基于多级暂堵转向压裂机理研发了新型暂堵材料，形成了多级暂堵转向压裂技术，新疆低渗透油田应用该技术后，产量得到大幅提高；Tan Xuebao等人[19]对暂堵球运移模型进行了改进，使其适用于直井、斜井和水平井，并建立了暂堵球坐封效率的计算公式。
虽然暂堵球的受力情况及其在井筒中的运移规律得到了一定的研究，但关于暂堵球在水平井中的运移及封堵行为特征的研究较少。目前工程中对暂堵球的投放依旧以现场试验为主，而数值模拟能够有效弥补现场试验的缺陷。一些学者也针对暂堵球运移开展了数值模拟研究，Li Xiaohe等人[20]建立了暂堵球综合运移模型，研究了影响井筒暂堵的因素，并验证了水平井暂堵的可能性；张锋等人[21]基于CFD-DPM建立了暂堵球运移模型，分析了暂堵球的运移机理和坐封规律；张雄等人[22]基于复合暂堵压裂机理开展了暂堵压裂数值模拟，优选了暂堵材料，优化了暂堵压裂施工参数，并在塔河油田进行了应用，取得了良好成效；R.W.Brown等人[23]建立了暂堵球在井筒中运移的模型，探究了泵注排量与流体黏度对暂堵球坐封的影响；周彤等人[24]利用边界元方法，建立了水平井“井筒–射孔炮眼–裂缝扩展”耦合模型，提出了压裂过程中暂堵球分配的计算方法，模拟了非均质场条件下暂堵球数量、投球时机和投球次数对于裂缝扩展的影响；达引朋等人[25]基于三维地质建模分析了含水井调堵压裂增产机理，根据暂堵压裂数值模拟结果优化了暂堵施工参数，并在长庆油田进行了应用，暂堵后缝内压力明显提升；Cheng Wan等人[26]采用数值模拟方法追踪了暂堵球在螺旋射孔簇水平井中的运移轨迹，分析了暂堵球密度、注入速度及射孔效率对暂堵球坐封效率的影响。
对比各种模拟方法的特征发现，常规离散相模型（DPM）将暂堵球视为质点，在求解过程中忽略了暂堵球的体积及暂堵球自身旋转运动的影响[27]，导致模拟结果误差较大，而CFD-DEM耦合模型能有效解决上述问题。考虑暂堵球颗粒直径相对较大，笔者基于CFD-DEM耦合模型，建立了页岩气水平井井筒暂堵模型，模拟了暂堵球在页岩气水平井中的运移过程，研究了暂堵球的运移规律及暂堵球坐封影响因素，从而明确暂堵球坐封孔眼的条件，提升暂堵球坐封效率，为页岩气水平井暂堵压裂施工提供了理论支撑。
1. 页岩气水平井井筒暂堵模型的建立
1.1 数学模型
采用CFD-DEM耦合模型模拟暂堵球在页岩气水平井中的运移时，将液相视为连续相，在欧拉坐标系下求解纳维–斯托克斯方程；将暂堵球视为离散相，在拉格朗日坐标系下求解运动方程。
1.1.1 流体控制方程
由于在孔眼附近压裂液呈紊流状态，因此选择湍流模型作为流体流动模型，故压裂液流动由连续性方程及N-S方程控制。连续性方程为：
∂ρ∂t+∇(ρu)=0 (1) 动量守恒方程为：
\frac{\partial (\rho u)}{\partial t}+\nabla (\rho u)=-\nabla p+{\boldsymbol{\nabla}} \tau +\rho g+S_{\rm{M}} (2) 根据标准k-ε湍流模型，不可压缩湍流的附加方程为：
\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \nabla \left( {\rho ku} \right) = \nabla \left[ {\left( {\mu + \frac{{{\mu _{\text{t}}}}}{{{\sigma _k}}}} \right)\nabla k} \right] + {G_k} - G_b - \rho \varepsilon {{ - }}Y_{\rm{M}} + {S_k} (3) \begin{split} \frac{\partial(\rho \varepsilon)}{\partial t}+\nabla(\rho \varepsilon u)=&\nabla\left[\left(\mu+\frac{\mu_{\varepsilon}}{\sigma_{\varepsilon}}\right) \nabla \varepsilon\right]+C_{1 \varepsilon} \frac{\varepsilon}{k}\left(G_k+C_{3 \varepsilon} G_0\right)-\\ &C_{2 \varepsilon} \rho \frac{\varepsilon^2}{k}+S_{\varepsilon}\\[-10pt] \end{split} (4) 式中：ρ为流体密度，kg/m3；t为时间，s；u为瞬时速度，m/s；p为压力，Pa；
\tau 为应力张量，kg/（m·s2）；g为重力加速度，m/s2；SM为固液动量交换损失，kg·m/s；\mu 为层流黏度，Pa·s；{\mu _{\text{t}}} 为湍流黏度，Pa·s；k为紊流脉动动能，J；Gk为平均速度梯度引起的湍流动能，J；Gb为由浮力产生的湍流动能，J；\varepsilon 为紊流脉动动能的耗散率，%；YM为可压缩湍流中波动膨胀对总耗散率的贡献；C1ε，C2ε和C3ε为常数，C1ε=1.44，C2ε=1.92；σk和σε分别为k和ε的湍流普朗特数，σk=1.0，σε=1.3；Sk和Sε为用户定义的源项。1.1.2 离散相控制方程
暂堵球作为离散相，遵守牛顿第二定律，可以将暂堵球的运动分解为平滑运动与翻转运动。暂堵球的运动方程[28]为：
m_{\mathrm{b}} \frac{\mathrm{d} u_{\mathrm{b}}}{\mathrm{d} t}=F_{\mathrm{w-b}}+F_{\mathrm{b-b}}-F_{\mathrm{f}}+m_{\mathrm{b}} g (5) I_{\mathrm{b}} \frac{\mathrm{d} \omega_{\mathrm{b}}}{\mathrm{d} t}=M_{\mathrm{b}} (6) 式中：mb为暂堵球的质量，kg；
u_{\rm{b}} 为暂堵球的平移速度，m/s；Ib为暂堵球的转动动量，kg·m2；{\omega _{\text{b}}} 为暂堵球的角速度，rad/s；Fw-b为壁面对暂堵球的作用力，N；Fb-b为暂堵球之间的作用力，N；Ff为流体对暂堵球的作用力；Mb为暂堵球所受力矩，N·m。1.1.3 连续相与离散相的耦合
计算模型中，暂堵球与流体之间的动量交换方程为：
S=\sum\left[\frac{0.75 \mu_{\mathrm{f}} C_{\mathrm{D}} Re}{\rho_{\mathrm{b}} d_{\mathrm{b}}{ }^2}\left(u_{\mathrm{b}}-u\right)+F_{\text {other }}\right] q_{\mathrm{b}} \Delta t (7) 式中：S为连续相到离散相的动量传递量，kg·m/s；μf为流体的黏度，Pa·s；ρb为暂堵球的密度kg/m3；db为暂堵球的直径，m；Re为相对雷诺数；u为暂堵球和流体的速度，m/s；CD为阻力系数；qb为暂堵球的质量流量，kg/s；Δt为时间步长，s；Fother代表单位质量其他作用力，N/kg。
暂堵球与流体之间的质量交换方程为：
V = \frac{{\Delta {q_{\text{b}}}}}{{{m_{\text{b},0}}}}{q_{\text{b},0}} (8) 式中：V为离散相到连续相的质量传递量，kg/s2；Δqb、qb，0分别为暂堵球的质量流量改变量、暂堵球注入的初始质量流量，kg/s；mb,0为暂堵球的初始质量，kg。
1.2 物理模型
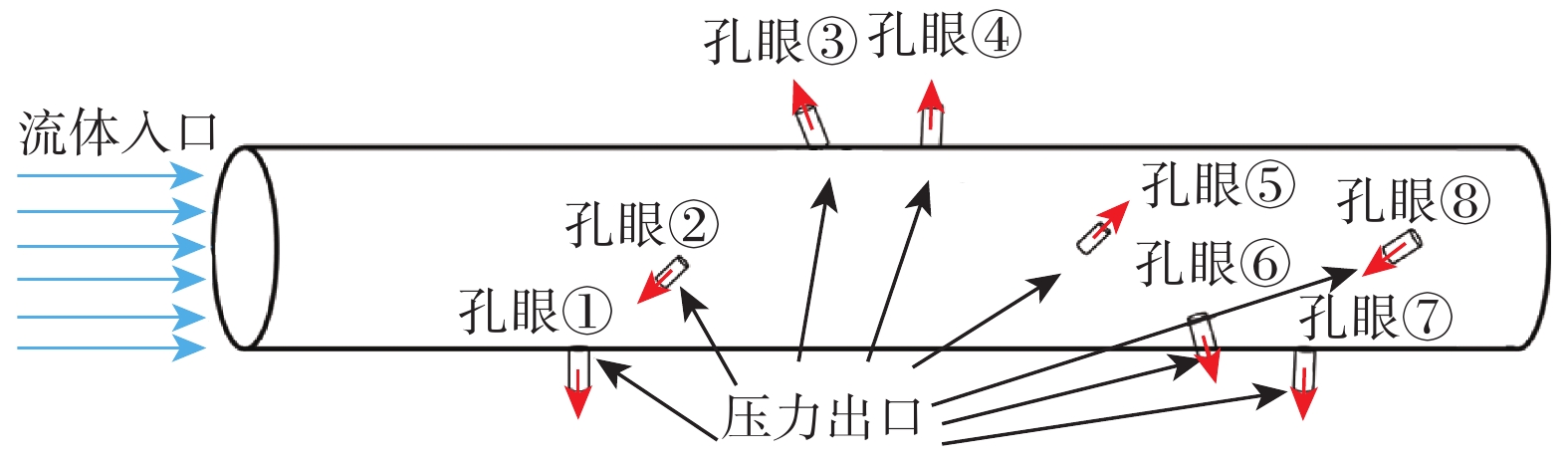
页岩储层等非常规油气藏压裂时多采用水平井进行套管注入，基于现场施工数据以ϕ139.7 mm套管为研究对象。由于建立完整的井筒模型，需要划分的网格数量过多，计算速度慢，为了提升效率，节约计算资源，建立了典型的单段射孔段套管模型，对单簇射孔段进行模拟。模型总长度1.00 m，套管入口距离射孔段0.40 m，射孔段长度0.50 m，套管外径为139.7 mm，内径为114.3 mm，从左至右8个孔眼的编号为①，②，…，⑧，射孔沿套管表面呈螺旋分布，孔眼直径为9.5 mm，孔眼相位角为60°，孔眼密度为16孔/m，如图1所示。
在CFD-DEM耦合的页岩气水平井井筒暂堵物理模型中建立暂堵球球体模型时，考虑了暂堵球自身的体积及旋转运动对暂堵球运移坐封的影响，同时将暂堵球与井筒壁面的接触形式设置为反弹，并考虑了暂堵球碰击孔眼后从孔眼脱落的情况。而以往的研究则将暂堵球视为质点，忽略暂堵球体积以及自身的旋转运动对暂堵球运移的影响，认为从孔眼流出的质点便是坐封在孔眼上的暂堵球，与之相比，该模型能更准确地反映暂堵球在水平射孔段的运移坐封情况。模型边界条件设置如图2所示，套管入口边界条件设置为“速度入口”，孔眼出口边界条件设置为“压力出口”，泵注排量设置为1～13 m3/min，暂堵球初始注入速度与压裂液速度一致，压裂液密度为1 000 kg/m3，压裂液黏度为1 mPa·s，暂堵球密度分别为900，1020和1200 kg/m3，暂堵球数量为1/10个。
2. 模拟结果分析与讨论
2.1 暂堵球运动过程分析
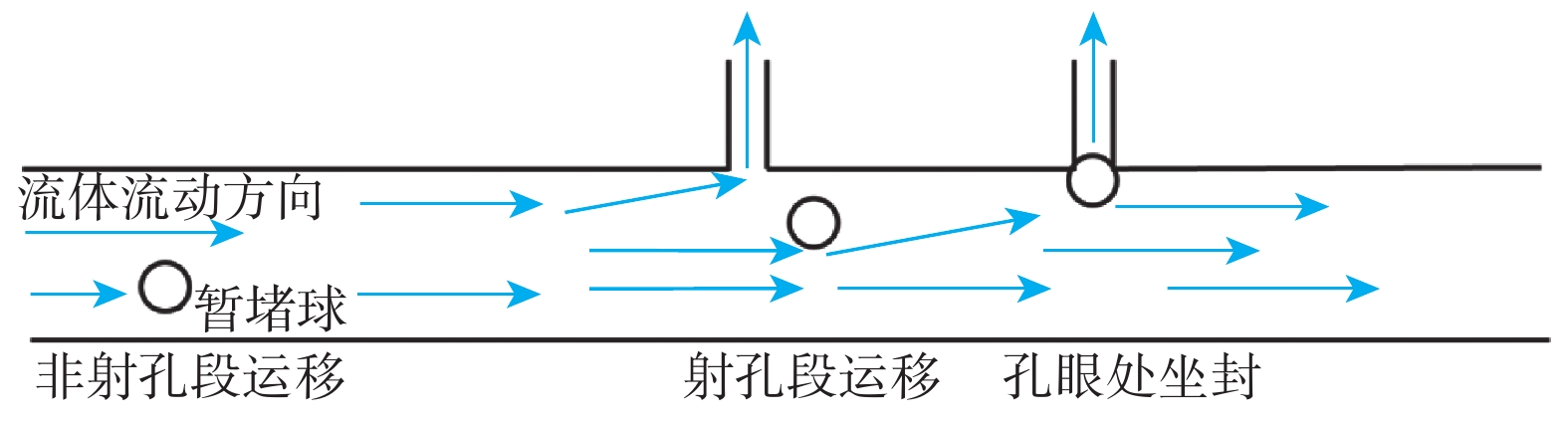
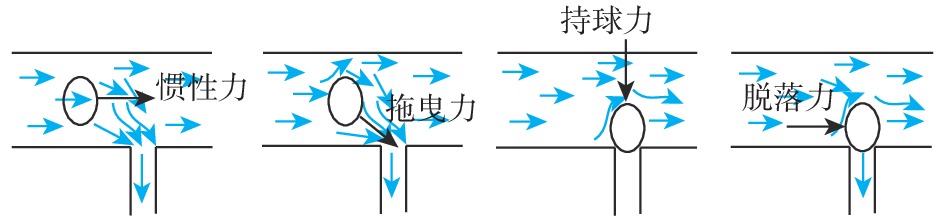
井筒暂堵是指储层改造过程中向井筒中泵注含有暂堵球的压裂液，暂堵球随压裂液运移到水平井射孔段，并坐封在孔眼上封堵孔眼，从而使压裂液转向未改造的储层段[29]。暂堵球在水平井中运移直至坐封在孔眼上主要分为3个阶段（见图3）：非射孔段运移、射孔段运移、孔眼坐封。暂堵球在孔眼处的受力主要为拖曳力、惯性力、持球力、脱落力（见图4）。当拖曳力大于惯性力时，暂堵球被流体携带向孔眼方向运移，而暂堵球坐封在孔眼上时主要受到来自于射孔压差的持球力和管内流体作用在暂堵球上的脱落力，当持球力大于脱落力时，暂堵球才会坐封在孔眼上[30]。
惯性力的计算公式为：
{F_{\text{G}}} = \frac{1}{6}{\text{π }}{d_{\text{b}}}^3{\rho _{\text{b}}}\frac{{{\text{d}}{u_{\text{b}}}}}{{{\text{d}}t}}{\text{ }} (9) 拖曳力的计算公式为：
{F_{\text{r}}} = \frac{{u_{\text{p}}}^2}{8} \frac{{\text{π }}{d_{\text{b}}}^2}{4} \rho K_{\text{d}}= \frac{{\rho {\text{π }}K_{\text{d}}{d_{{\text{b}}}^2}}{u_{\text{p}}}^2}{32} (10) 持球力的计算公式为：
{F_{\text{H}}}{\text{=}}\frac{{\text{π}}}{4}{d_{\text{b}}}^2\Delta p = \frac{\rho {\text{π }}{d_{\text{b}}}^2}{8}{(u_{\text{b}}-u_{\text{b}})}^2 = \frac{\rho {\text{π}} d^2_{\rm{b}}}{8}(u_{\rm{b}}-u_{\rm{p}})^2 (11) 脱落力的计算公式为：
{F_{\text{u}}} = 5.28 \times {10^{ - 3}}{f_{\text{d}}}\rho {u_{\text{b}}}^2\ \left[{d_{\text{b}}}^2 - \frac{{{d_{\text{b}}}^2\sin \theta }}{{180}} + \frac{{{d_{\text{p}}}}}{{\text{π }}}{({d_{\text{b}}}^2 - {d_{\text{P}}}^2)^{1/2}}\right] (12) \;其中\qquad\qquad\qquad \sin \theta = \frac{{{d_{\text{p}}}}}{{d_{\text{b}}}}\qquad\qquad (13) 式中：Δp为孔眼压差，MPa；dp为孔眼直径，m；fd为阻力因子；FG为暂堵球受到的惯性力，N；Fr为暂堵球受到流体的拖曳力，N；Kd为拖曳力系数；FH为暂堵球受到的孔眼压差形成的持球力，N；Fu为暂堵球受到来流冲击的脱落力，N。
2.1.1 单个暂堵球运移封堵特征分析
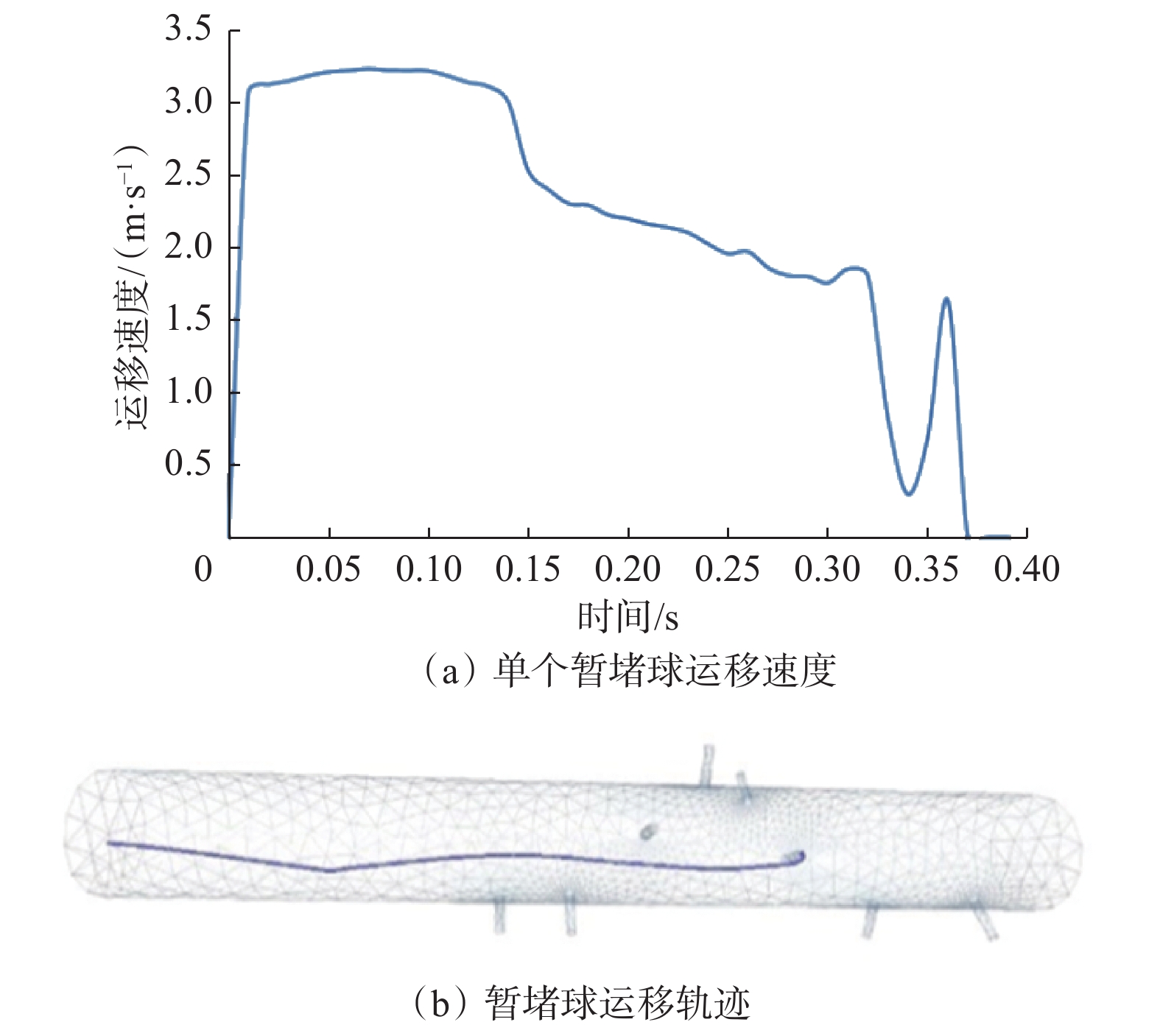
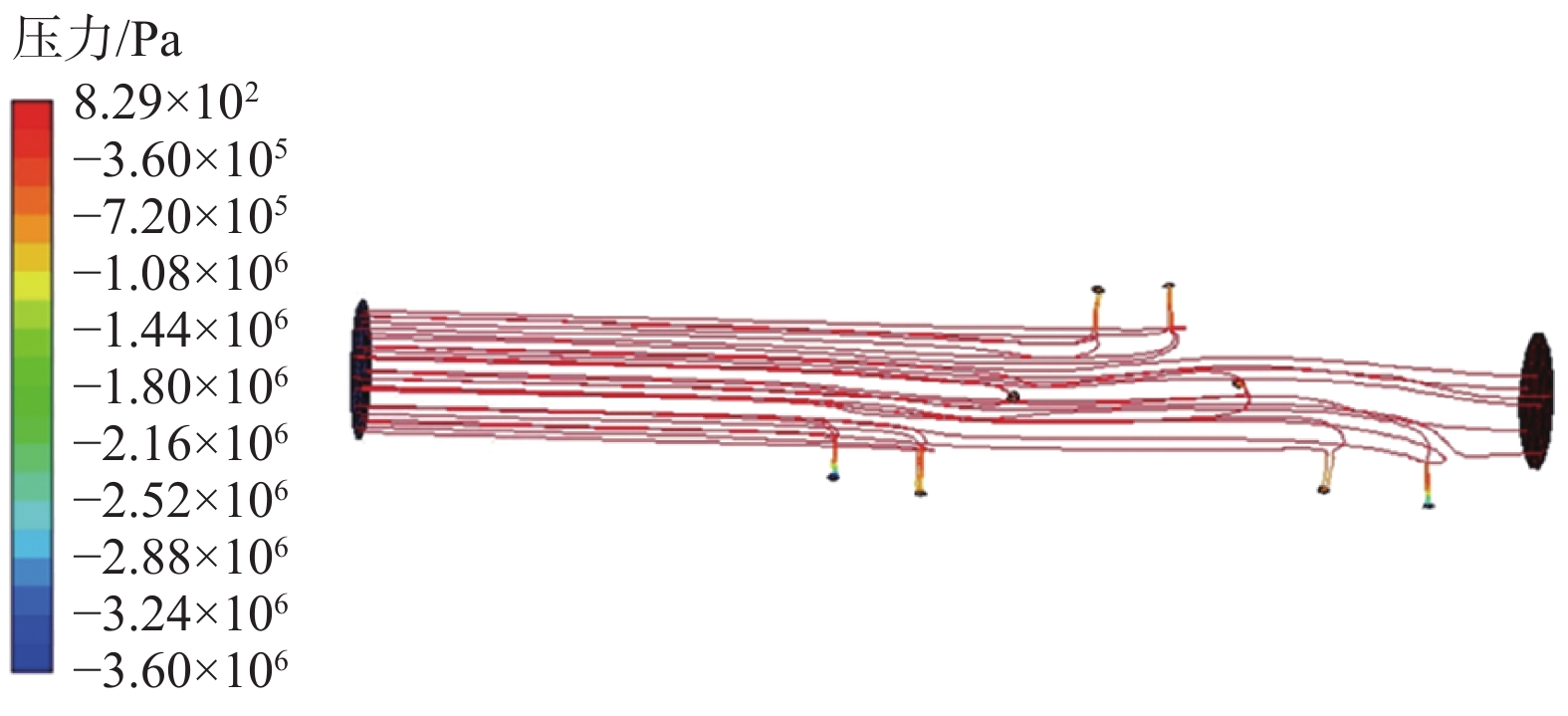
采用CFD-DEM耦合方法，可以对暂堵球在页岩气水平井中的运移过程进行可视化数值模拟，泵注排量设置为2 m3/min，暂堵球初始运移速度设置为3.05 m/s（与流体速度一致），对单个高密度暂堵球的运动过程进行分析，其中暂堵球运移速度变化及暂堵球运移轨迹如图5所示，某时刻暂堵球运移位置如图6所示，流场压力流线如图7所示。
从图5（a）和图6（a）可以看出：暂堵球进入射孔段之前（t<0.1 s），其运移速度略微增大，因为在未进入射孔段之前，暂堵球与流体流动方向一致，流体对于暂堵球存在一定的推动作用，使暂堵球运移速度升高，暂堵球能更快进入射孔段；暂堵球在进入射孔段后，其运移速度略微降低，因为暂堵球运移速度大于流体速度后，流体对暂堵球存在一定的阻力作用，使暂堵球运移速度降低。从图5（a）和图6（b）可以看出，暂堵球进入射孔段后（t>0.14 s），由于流体不断从孔眼流出，井筒内流量减小，暂堵球运移速度显著降低，导致惯性力降低。同时，结合图7可以看出，由于流体不断从孔眼流向储层，在孔眼处形成负压差，从而对暂堵球产生拖曳力，使暂堵球在流体携带作用下向孔眼附近运移（见图5（b））。从图5（a）和图6（c）可以看出，因为孔眼截面积较小，暂堵球被流体携带至孔眼附近时，暂堵球运移速度有所升高，使暂堵球因井筒流量降低而导致其运移速度降低的趋势减缓，但在离开孔眼拖曳力作用范围后暂堵球运移速度显著降低。从图5（a）和图6（d）可以看出，当暂堵球运移至⑥号孔眼处时，暂堵球速度因为孔眼截面减小而增大，并且以较大的速度碰击孔眼⑥，因为受到孔眼压差的束缚作用，暂堵球运移速度降低至0，从而坐封在孔眼⑥上。
![]()
图 6 特定时刻单个暂堵球的运移位置示意Figure 6. Movement position of a ball sealer at a specific moment2.1.2 多个暂堵球运移封堵特征分析
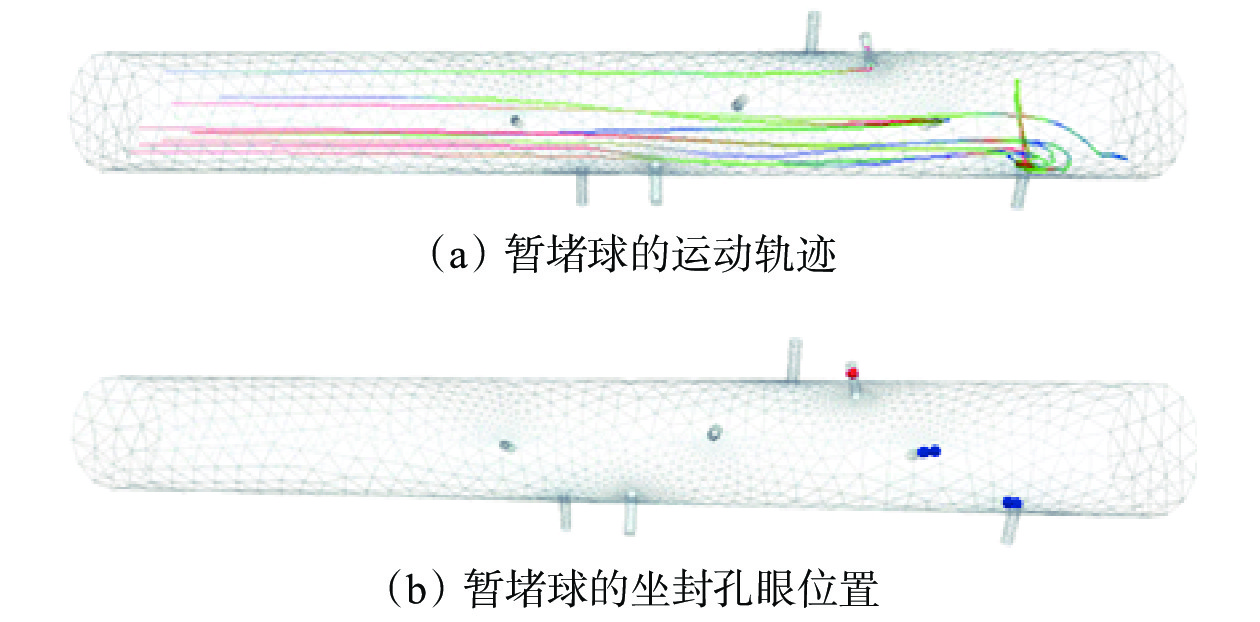
页岩储层在进行暂堵转向压裂施工时，一般采用多个暂堵球对多个孔眼坐封，因此，采用数值模拟分析多个暂堵球的运移坐封过程。泵注排量设置为6 m3/min，暂堵球速度设置为9.14 m/s（与流体速度一致），对多个低密度暂堵球的运动过程进行模拟分析，其中暂堵球的运移轨迹与坐封孔眼位置如图8所示，坐封在不同孔眼上暂堵球的运移速度如图9所示，某时刻暂堵球的运移位置如图10所示，流场压力流线如图11所示。
![]()
图 8 多个暂堵球的运动轨迹与坐封孔眼位置Figure 8. Migration trajectory of ball sealers and sealed perforation position![]()
图 9 坐封在不同孔眼上暂堵球的运移速度Figure 9. Migration speed of ball sealers on different perforations从图8（b）可以看出，排量为6 m3/min时，暂堵球能坐封在孔眼⑥、⑦和⑧上，因此适当增加暂堵球数量，有利于增加坐封孔眼数量，提升井筒暂堵效果。结合图9、图10（a）和图10（b）可知，暂堵球进入射孔段前（t<0.04 s），暂堵球的运移速度有所增大，因为在该时间段内暂堵球与流体流动方向一致，流体对暂堵球有一定推动作用，使暂堵球运移速度有所升高，随后由于流体速度比暂堵球运移速度低，对暂堵球产生阻力作用，暂堵球运移速度略微降低；暂堵球进入射孔段后（t>0.05 s），由于流体不断从孔眼流向储层，井筒内流量降低，暂堵球运移速度降低，惯性力也降低。从图8（a）和图11可以看出，流体从孔眼流出，在孔眼处形成了负压差，产生了拖曳力，使暂堵球在流体携带作用下向孔眼运移，便于暂堵球坐封在孔眼上。从图10（c）、图10（d）、图10（e）可以看出，t=0.10，0.15和0.18 s时，暂堵球逐渐坐封在孔眼⑥、⑦和⑧上，结合图9分析得到暂堵球被流体携带至孔眼⑥、⑦和⑧附近时，由于孔眼截面较小，暂堵球运移速度有所升高，使暂堵球因井筒流量降低，导致其运移速度降低的趋势有所减缓，同时能以较大的运移速度碰击孔眼⑥、⑦和⑧，并且在孔眼压差束缚下暂堵球运移速度降低至0，从而坐封在孔眼⑥、⑦和⑧上。
2.2 暂堵球运移坐封影响因素分析
2.2.1 暂堵球直径对暂堵球运移以及坐封的影响
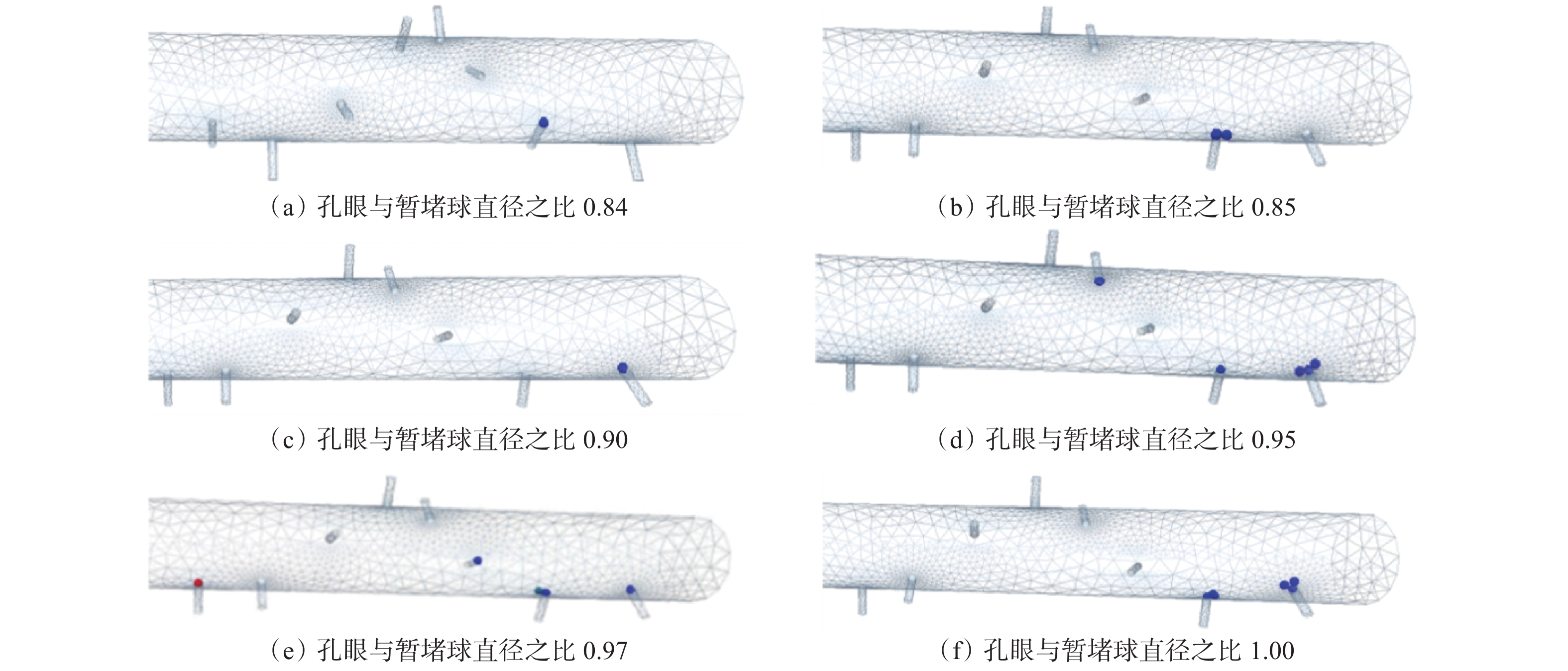
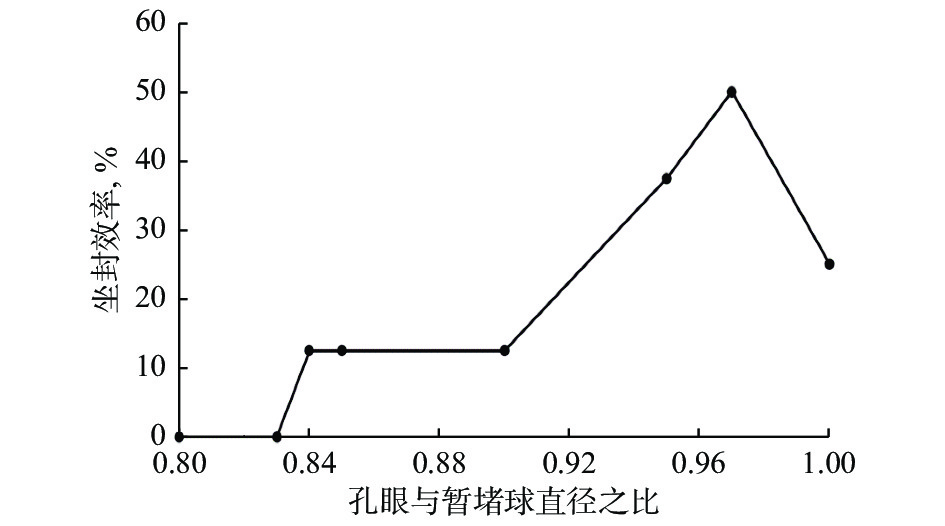
暂堵球在孔眼处的坐封一般经历封堵、溶胀和变形3个过程，因此暂堵球直径不能小于孔眼直径，否则暂堵球直接从孔眼流出而无法坐封在孔眼上[31]。暂堵球的直径对暂堵球受到的重力、拖曳力、惯性力等均有影响，因此基于数值模拟研究暂堵球直径对于暂堵球运移和坐封的影响。暂堵球直径设置为9.5～19.0 mm，泵注排量为4 m3/min，模拟孔眼直径与暂堵球直径之比在0.5～1.0条件下暂堵球运移坐封情况，暂堵球坐封孔眼模拟结果见表1和图12，坐封效率（坐封孔眼数量与孔眼总数量之比）和孔眼与暂堵球直径之比的关系如图13所示。
表 1 暂堵球直径对暂堵球运移及封堵行为的影响Table 1. Influence of ball sealer diameter on migration and sealing behavior of ball sealer排量/
（m3·min−1）孔眼直径/
mm暂堵球直径/
mm孔眼与暂堵球
直径之比暂堵球坐
封孔眼4 9.5 19.0 0.50 4 9.5 15.8 0.60 4 9.5 13.6 0.70 4 9.5 12.7 0.75 4 9.5 11.9 0.80 4 9.5 11.4 0.83 4 9.5 11.3 0.84 ⑦ 4 9.5 11.2 0.85 ⑦ 4 9.5 10.6 0.90 ⑧ 4 9.5 10.0 0.95 ⑤、⑦、⑧ 4 9.5 9.8 0.97 ①、⑥、⑦、⑧ 4 9.5 9.5 1.00 ⑦、⑧ ![]()
图 12 暂堵球直径对暂堵球运移及封堵行为的影响Figure 12. Influence of ball sealer diameter on migration and sealing behavior of ball sealer![]()
图 13 坐封效率和孔眼与暂堵球直径之比的关系Figure 13. Relationship between sealing efficiency and ratio of perforation diameter to ball sealer diameter结合表1、图12和图13可知：孔眼与暂堵球直径之比大于0.83时，暂堵球才能坐封在孔眼上；孔眼与暂堵球直径之比小于0.97时，由于暂堵球受到的阻力与暂堵球直径的平方成正比，此时暂堵球直径增大，暂堵球所受阻力也随之增加，且增加得更快，使暂堵球坐封难度增大，坐封效率降低；孔眼与暂堵球直径之比为0.97时，暂堵球坐封孔眼数量最多，坐封效率最高；孔眼与暂堵球直径之比大于0.97时，随着暂堵球直径增大，流体对暂堵球的拖曳力增大，使暂堵球更容易向孔眼处运移，暂堵球坐封效果更好。
2.2.2 泵注排量对暂堵球运移以及坐封的影响
暂堵球在孔眼处坐封主要受惯性力、拖曳力、持球力和脱落力的影响[26]。当拖曳力大于惯性力时，暂堵球被流体携带向孔眼附近运移，只有当持球力大于脱落力时，暂堵球才能坐封在孔眼上，不会在来流的冲击下从孔眼脱落[13]；而惯性力、拖曳力、持球力及脱落力均与泵注排量有关，因此基于数值模拟分析泵注排量对暂堵球运移及坐封的影响。泵注排量设置为1～13 m3/min，选择低密度暂堵球（900 kg/m3）、中密度暂堵球（1 020 kg/m3）、高密度暂堵球（1 200 kg/m3），模拟不同密度暂堵球在不同泵注排量下的运移封堵情况，暂堵球坐封孔眼模拟结果见表2，暂堵球坐封效率与泵注排量的关系如图14所示。
表 2 泵注排量对暂堵球运移及封堵行为的影响Table 2. Influence of pump rate on migration and sealing behavior of ball sealer排量/
（m3·min−1）入口流速/
（m·s−1）不同密度暂堵球的坐封孔眼 低密度暂堵球 中密度暂堵球 高密度暂堵球 1 1.52 ⑥ ⑥ ⑥ 2 3.05 ⑥ ⑥ ⑥ 3 4.57 ⑥、⑧ ⑥、⑦ ⑦ 4 6.10 ①、⑥、⑦、⑧ ⑦、⑧ ⑥、⑦ 5 7.62 ⑤、⑦、⑧ ⑦、⑧ ⑥、⑧ 6 9.74 ⑥、⑦、⑧ ⑤、⑦、⑧ ①、⑦、⑧ 7 10.67 ⑦、⑧ ⑥、⑧ ⑦、⑧ 8 12.19 ⑤、⑦ ⑦、⑧ ⑦ 9 13.72 ⑧ ⑧ ⑦ 10 15.24 ⑦ ⑧ ⑧ 11 16.67 ⑦ 12 18.29 ⑥ 13 19.80 ![]()
图 14 暂堵球坐封效率与泵注排量的关系Figure 14. Relationship between sealing efficiency of ball sealer and pump rate从表2可以看出：暂堵球在水平井运移过程中，暂堵球坐封的孔眼大多位于水平段下半部分，表明重力对于暂堵球运移及封堵的影响较大，暂堵球投入井筒后，其在重力作用下沿着套管下半部分运移，并坐封在套管下半部分的孔眼上；只有采用低密度和中密度暂堵球才坐封在位于套管中上部的孔眼⑤上，因为此时暂堵球密度与流体密度相差较小，暂堵球在浮力作用下能在套管中部运移，从而能坐封在孔眼⑤上。从图14可以看出：暂堵球坐封效率随着泵注排量增大呈先升高后降低的趋势；在低泵注排量范围内（1～6 m3/min），逐渐增大泵注排量，有利于提升暂堵球坐封效率。这是因为在低泵注排量范围内，暂堵球所受惯性力较小，逐渐增大泵注排量，则孔眼流量增加，导致孔眼压差增大，拖曳力也会相应增大，流体更容易携带暂堵球向孔眼运移，并且在孔眼处，因为孔眼流量增大，持球力也会增大，因此暂堵球不容易从孔眼处脱落，坐封效率更高；当泵注排量持续增大时，暂堵球所受惯性力增大，并逐渐占主导地位，此时惯性力对于暂堵球运移的影响更大，因此暂堵球不易向孔眼运移，并且孔眼处来流的冲击力增强，脱落力增大，使暂堵球更容易从孔眼上脱落，导致坐封效率降低。从图14还可以看出，泵注排量在4～7 m3/min时，暂堵球的坐封效率相对较高。
2.2.3 暂堵球密度对暂堵球运移以及坐封的影响
水平井进行分段多簇压裂时，不同水平井段所采用的暂堵球密度可能不一致[32]，而暂堵球密度对于暂堵球所受重力和惯性力均有影响，从而影响暂堵球在水平段的运移。采用数值模拟方法，分析暂堵球密度对暂堵球运移及坐封的影响，结果见表3。
表 3 不同密度暂堵球在不同泵排量下的坐封效率Table 3. Sealing efficiency of ball sealers with different densities under different pump rates排量/
（m3·min−1）不同密度暂堵球的坐封效率，% 900 kg/m3 1020 kg/m3 1200 kg/m3 1 12.5 12.5 12.5 2 12.5 12.5 12.5 3 25.0 25.0 12.5 4 50.0 25.0 25.0 5 37.5 25.0 25.0 6 37.5 37.5 37.5 7 25.0 25.0 25.0 8 25.0 25.0 12.5 9 12.5 12.5 12.5 10 12.5 12.5 12.5 11 12.5 0 0 12 12.5 0 0 13 0 0 0 从表3可以看出：泵注排量为1～2 m3/min时，低、中、高密度暂堵球均能坐封在孔眼上，但坐封效率低，这是因为泵注排量小，暂堵球运移速度小，惯性力小，容易被流体携带向孔眼运移，但由于泵注排量小，各个孔眼流量低，孔眼压差小，暂堵球难以坐封在孔眼上，因此坐封效率低；泵注排量为3～8 m3/min时，暂堵球坐封效率明显升高，因为泵注排量增大后，孔眼流量增大，拖曳力增大，暂堵球更容易被流体携带至孔眼处，并且孔眼压差增大后各孔眼持球力增大，使坐封效率升高；泵注排量为9～12 m3/min时，暂堵球运移速度增大，惯性力增加得更快，暂堵球运移轨迹难以发生改变，流体难以携带暂堵球至孔眼处，此外泵注排量增大后，井筒内流体对孔眼处暂堵球产生的脱落力增大，使坐封效率降低；泵注排量大于13 m3/min时，暂堵球运移速度极大，在惯性力的作用下流体几乎对暂堵球没有影响，暂堵球直接经过射孔段流出井筒而无法坐封在孔眼上。从表3还可以看出：低密度暂堵球坐封在孔眼上的泵注排量范围最大，中密度暂堵球次之，高密度暂堵球最小；在中等排量范围内，3种密度暂堵球的坐封效率均较高，但低密度暂堵球的坐封效率普遍比中密度暂堵球和高密度暂堵球高，综合分析认为，暂堵球的密度越大，暂堵球的重力越大，则暂堵球受到的惯性力越大，从而导致暂堵球在运移过程中流体对暂堵球的携带能力减弱，其运动轨迹难以发生改变，暂堵球不易向孔眼运移，坐封效率不高。
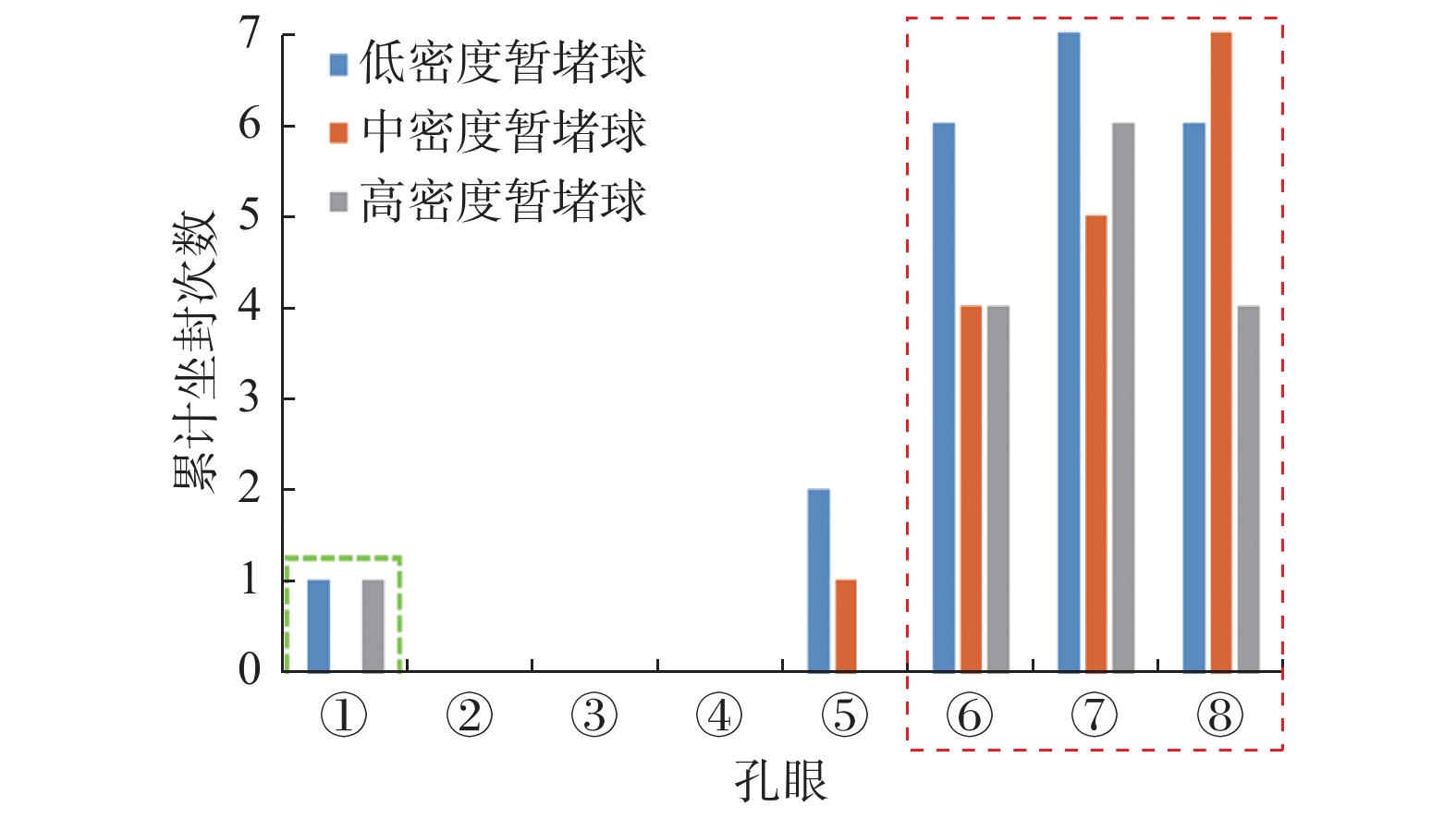
2.3 暂堵球坐封孔眼位置特征分析
对暂堵球运移轨迹进行分析发现，暂堵球在孔眼处的运动存在2种情况：1）暂堵球碰击孔眼之后恰好坐封在孔眼上；2）暂堵球碰击孔眼之后在孔眼处短暂停留，随后在来流的冲击作用下从孔眼脱离继续流动，导致暂堵球无法坐封在孔眼上。对孔眼坐封次数进行统计，结果如图15所示。从图15可以看出，暂堵球在页岩气水平井射孔段运移时最容易坐封在射孔簇最后3个孔眼处（见图2），因为流体不断从孔眼中流出，使射孔段后半部分井筒的流量和流速降低，暂堵球运移速度及其所受惯性力更小，暂堵球容易被流体携带向孔眼运移，因此更容易在射孔簇后半段的孔眼坐封。此外，暂堵球易坐封在第1个孔眼上，其原因是暂堵球刚进入射孔簇时，惯性力较大，并且在拖曳力作用下，暂堵球以较高的速度碰击第1个孔眼，由于其直径较大，所以容易被该孔眼卡住从而坐封在其上。
![]()
图 15 孔眼暂堵球坐封次数统计结果Figure 15. Statistical results of sealing times of perforation by ball sealer3. 结 论
1）暂堵球在页岩气水平井运移过程中，进入射孔段之前，暂堵球在流体的推动作用下运移速度增大，暂堵球加速进入射孔段。进入射孔段之后，由于流体不断从孔眼流向储层，在孔眼处产生拖曳力，而井筒内流量降低，使暂堵球运移速度逐渐降低，惯性力随之降低，因此在拖曳力作用下，暂堵球更容易被流体携带至孔眼附近；由于孔眼截面较小，孔眼附近的暂堵球运移速度升高，减缓了暂堵球因为井筒流量降低而导致运移速度降低的趋势，暂堵球运移速度变化幅度变小，同时也有利于暂堵球以较大的运移速度碰击孔眼从而坐封在孔眼上。
2）孔眼与暂堵球直径之比小于0.83时，暂堵球在来流冲击作用下无法坐封在孔眼上；孔眼与暂堵球直径之比大于0.83时，随着孔眼与暂堵球直径之比增大，暂堵球的坐封效率呈现先升高后降低的趋势；孔眼与暂堵球直径之比为0.97时，暂堵球坐封孔眼的数量最多，暂堵球的坐封效率最高。
3）暂堵球坐封效率随着泵注排量增加呈先升高后降低的趋势。泵注排量较低时（1～6 m3/min），逐渐增大泵注排量，暂堵球坐封效率升高；当排量持续增加时，暂堵球的惯性力增加，此时暂堵球的运移轨迹不易发生改变，坐封效率降低；泵注排量为4～7 m3/min时，暂堵球坐封效率相对较高。
4）低密度暂堵球坐封效果最好，高密度暂堵球坐封效果最差。
5）暂堵球最容易坐封在射孔簇后半段孔眼处，也能坐封在第1个孔眼上。
-
![]()
图 6 特定时刻单个暂堵球的运移位置示意
Figure 6. Movement position of a ball sealer at a specific moment
![]()
图 8 多个暂堵球的运动轨迹与坐封孔眼位置
Figure 8. Migration trajectory of ball sealers and sealed perforation position
![]()
图 9 坐封在不同孔眼上暂堵球的运移速度
Figure 9. Migration speed of ball sealers on different perforations
![]()
图 12 暂堵球直径对暂堵球运移及封堵行为的影响
Figure 12. Influence of ball sealer diameter on migration and sealing behavior of ball sealer
![]()
图 13 坐封效率和孔眼与暂堵球直径之比的关系
Figure 13. Relationship between sealing efficiency and ratio of perforation diameter to ball sealer diameter
![]()
图 14 暂堵球坐封效率与泵注排量的关系
Figure 14. Relationship between sealing efficiency of ball sealer and pump rate
![]()
图 15 孔眼暂堵球坐封次数统计结果
Figure 15. Statistical results of sealing times of perforation by ball sealer
表 1 暂堵球直径对暂堵球运移及封堵行为的影响
Table 1 Influence of ball sealer diameter on migration and sealing behavior of ball sealer
排量/
（m3·min−1）孔眼直径/
mm暂堵球直径/
mm孔眼与暂堵球
直径之比暂堵球坐
封孔眼4 9.5 19.0 0.50 4 9.5 15.8 0.60 4 9.5 13.6 0.70 4 9.5 12.7 0.75 4 9.5 11.9 0.80 4 9.5 11.4 0.83 4 9.5 11.3 0.84 ⑦ 4 9.5 11.2 0.85 ⑦ 4 9.5 10.6 0.90 ⑧ 4 9.5 10.0 0.95 ⑤、⑦、⑧ 4 9.5 9.8 0.97 ①、⑥、⑦、⑧ 4 9.5 9.5 1.00 ⑦、⑧ 
下载: 导出CSV
表 2 泵注排量对暂堵球运移及封堵行为的影响
Table 2 Influence of pump rate on migration and sealing behavior of ball sealer
排量/
（m3·min−1）入口流速/
（m·s−1）不同密度暂堵球的坐封孔眼 低密度暂堵球 中密度暂堵球 高密度暂堵球 1 1.52 ⑥ ⑥ ⑥ 2 3.05 ⑥ ⑥ ⑥ 3 4.57 ⑥、⑧ ⑥、⑦ ⑦ 4 6.10 ①、⑥、⑦、⑧ ⑦、⑧ ⑥、⑦ 5 7.62 ⑤、⑦、⑧ ⑦、⑧ ⑥、⑧ 6 9.74 ⑥、⑦、⑧ ⑤、⑦、⑧ ①、⑦、⑧ 7 10.67 ⑦、⑧ ⑥、⑧ ⑦、⑧ 8 12.19 ⑤、⑦ ⑦、⑧ ⑦ 9 13.72 ⑧ ⑧ ⑦ 10 15.24 ⑦ ⑧ ⑧ 11 16.67 ⑦ 12 18.29 ⑥ 13 19.80
下载: 导出CSV
表 3 不同密度暂堵球在不同泵排量下的坐封效率
Table 3 Sealing efficiency of ball sealers with different densities under different pump rates
排量/
（m3·min−1）不同密度暂堵球的坐封效率，% 900 kg/m3 1020 kg/m3 1200 kg/m3 1 12.5 12.5 12.5 2 12.5 12.5 12.5 3 25.0 25.0 12.5 4 50.0 25.0 25.0 5 37.5 25.0 25.0 6 37.5 37.5 37.5 7 25.0 25.0 25.0 8 25.0 25.0 12.5 9 12.5 12.5 12.5 10 12.5 12.5 12.5 11 12.5 0 0 12 12.5 0 0 13 0 0 0
下载: 导出CSV
-
[1] 雷群,杨战伟,翁定为,等. 超深裂缝性致密储集层提高缝控改造体积技术:以库车山前碎屑岩储集层为例[J]. 石油勘探与开发,2022,49(5):1012–1024. LEI Qun, YANG Zhanwei, WENG Dingwei, et al. Techniques for improving fracture-controlled stimulated reservoir volume in ultra-deep fractured tight reservoirs: a case study of Kuqa piedmont clastic reservoirs, Tarim Basin, NW China[J]. Petroleum Exploration and Development, 2022, 49(5): 1012–1024.
[2] 蒋廷学. 非常规油气藏新一代体积压裂技术的几个关键问题探讨[J]. 石油钻探技术,2023,51(4):184–191. JIANG Tingxue. Discussion on several key issues of the new-generation network fracturing technologies for unconventional reservoirs[J]. Petroleum Drilling Techniques, 2023, 51(4): 184–191.
[3] 冯发勇,梁志彬,姚昌宇. 东胜气田锦30井区变黏压裂液体积压裂技术[J]. 石油钻采工艺,2022,44(6):740–745. FENG Fayong, LIANG Zhibin, YAO Changyu. SRV-oriented fracturing with viscosity-variable fracturing fluids in the Jin-30 Well District, Dongsheng Gas Field[J]. Oil Drilling & Production Technology, 2022, 44(6): 740–745.
[4] 郑新权,何春明,杨能宇,等. 非常规油气藏体积压裂2.0工艺及发展建议[J]. 石油科技论坛,2022,41(3):1–9. ZHENG Xinquan, HE Chunming, YANG Nengyu, et al. Volumetric fracturing 2.0 process for unconventional oil and gas reservoirs and and R&D suggestions[J]. Petroleum Science and Technology Forum, 2022, 41(3): 1–9.
[5] 熊春明,石阳,周福建,等. 深层油气藏暂堵转向高效改造增产技术及应用[J]. 石油勘探与开发,2018,45(5):888–893. XIONG Chunming, SHI Yang, ZHOU Fujian, et al. High efficiency reservoir stimulation based on temporary plugging and diverting for deep reservoirs[J]. Petroleum Exploration and Development, 2018, 45(5): 888–893.
[6] 郭建春,赵峰,詹立,等. 四川盆地页岩气储层暂堵转向压裂技术进展及发展建议[J]. 石油钻探技术,2023,51(4):170–183. GUO Jianchun, ZHAO Feng, ZHAN Li, et al. Recent advances and development suggestions of temporary plugging and diverting fracturing technology for shale gas reservoirs in the Sichuan Basin[J]. Petroleum Drilling Techniques, 2023, 51(4): 170–183.
[7] 王磊,盛志民,赵忠祥,等. 吉木萨尔页岩油水平井大段多簇压裂技术[J]. 石油钻探技术,2021,49(4):106–111. WANG Lei, SHENG Zhimin, ZHAO Zhongxiang, et al. Large-section and multi-cluster fracturing technology for horizontal wells in the Jimsar shale oil reservoir[J]. Petroleum Drilling Techniques, 2021, 49(4): 106–111.
[8] 杨恒林,吕嘉昕,谭鹏,等. 基于三维扫描技术的页岩暂堵压裂物理模拟实验[J]. 断块油气田,2022,29(1):118–123. YANG Henglin, LYU Jiaxin, TAN Peng, et al. Physical simulation experiment on shale temporary plugging and fracturing based on 3D scanning technology[J]. Fault-Block Oil & Gas Field, 2022, 29(1): 118–123.
[9] NOZAKI M, ZHU D, HILL A D D. Experimental and field data analyses of ball-sealer diversion[J]. SPE Production & Operations, 2013, 28(3): 286–295.
[10] 许江文,张谷畅,李建民,等. 暂堵剂形状对裂缝封堵影响规律的实验研究[J]. 断块油气田,2022,29(6):842–847. XU Jiangwen,ZHANG Guchang,LI Jianmin,et al. Experimental study on influence law of temporary plugging agent shape on fracture plugging[J]. Fault-Block Oil & Gas Field, 2022, 29(6): 842–847.
[11] 路智勇. 转向压裂用暂堵剂研究进展与展望[J]. 科学技术与工程,2020,20(31):12691–12701. LU Zhiyong. Progress and prospect study on temporary plugging agent for diverting fracturing[J]. Science Technology and Engineering, 2020, 20(31): 12691–12701.
[12] 肖晖,李洁,曾俊. 投球压裂堵塞球运动方程研究[J]. 西南石油大学学报(自然科学版),2011,33(5):162–167. XIAO Hui, LI Jie, ZENG Jun. Ball motion equation in the ball sealer fracturing[J]. Journal of Southwest Petroleum University (Science and Technology Edition), 2011, 33(5): 162–167.
[13] 蔡华,张光波,杨阳,等. 投球暂堵压裂工艺在煤层气井的应用[J]. 中国煤层气,2020,17(6):17–20. CAI Hua, ZHANG Guangbo, YANG Yang, et al. Application of ball temporary plugging fracturing technology in coalbed methane wells[J]. China Coalbed Methane, 2020, 17(6): 17–20.
[14] 刘明明, 马收, 刘立之, 等. 页岩气水平井压裂施工中暂堵球封堵效果研究[J]. 钻采工艺, 2020, 43(6):44−48. LIU Mingming, MA Shou, LIU Lizhi, et al. Study on the effect of temporary plugging ball in fracturing of horizontal shale gas well[J]. Drilling & Production Technology, 2020, 43(6): 44−48.
[15] 郑志兵. 暂堵球封堵效果影响因素分析及其在Z油田的应用[J]. 石化技术,2017,24(2):55–56. ZHENG Zhibing. Analysis on influencing factors of plugging effect and its application in Z Oilfield[J]. Petrochemical Industry Technology, 2017, 24(2): 55–56.
[16] 李春月,房好青,牟建业,等. 碳酸盐岩储层缝内暂堵转向压裂实验研究[J]. 石油钻探技术,2020,48(2):88–92. LI Chunyue, FANG Haoqing, MOU Jianye, et al. Experimental study on temporary fracture plugging and diverting fracturing of carbonate reservoirs[J]. Petroleum Drilling Techniques, 2020, 48(2): 88–92.
[17] 夏海帮. 页岩气井双暂堵压裂技术研究与现场试验[J]. 石油钻探技术,2020,48(3):90–96. XIA Haibang. The research and field testing of dual temporary plugging fracturing technology for shale gas wells[J]. Petroleum Drilling Techniques, 2020, 48(3): 90–96.
[18] 周丹,熊旭东,何军榜,等. 低渗透储层多级转向压裂技术[J]. 石油钻探技术,2020,48(1):85–89. ZHOU Dan, XIONG Xudong, HE Junbang, et al. Multi-stage deflective fracturing technology for low permeability reservoir[J]. Petroleum Drilling Techniques, 2020, 48(1): 85–89.
[19] TAN Xuebao, WENG Xiaowei, AHMED T K, et al. An improved ball sealer model for well stimulation[R]. SPE 189573, 2018.
[20] LI Xiaohe, CHEN Zhongmin, CHAUDHARY S, et al. An integrated transport model for ball-sealer diversion in vertical and horizontal wells[R]. SPE 96339, 2005.
[21] 张峰,荣莽,许明标. 页岩气水平井暂堵球运移坐封机理[J]. 科学技术与工程,2020,20(6):2202–2208. ZHANG Feng, RONG Mang, XU Mingbiao. Mechanism of temporary blocking ball’s transportation and blocking in shale gas horizontal wells[J]. Science Technology and Engineering, 2020, 20(6): 2202–2208.
[22] 张雄,耿宇迪,焦克波,等. 塔河油田碳酸盐岩油藏水平井暂堵分段酸压技术[J]. 石油钻探技术,2016,44(4):82–87. ZHANG Xiong, GENG Yudi, JIAO Kebo, et al. The technology of multi-stage acid fracturing in horizontal well for carbonate reservoir by temporary plugging ways in the Tahe Oilfield[J]. Petroleum Drilling Techniques, 2016, 44(4): 82–87.
[23] BROWN R W, NEILL G H, LOPER R G. Factors Influencing optimum ball sealer performance[J]. Journal of Petroleum Technology, 1963, 15(4): 450–454. doi: 10.2118/553-PA
[24] 周彤,陈铭,张士诚,等. 非均匀应力场影响下的裂缝扩展模拟及投球暂堵优化[J]. 天然气工业,2020,40(3):82–91. ZHOU Tong, CHEN Ming, ZHANG Shicheng, et al. Simulation of fracture propagation and optimization of ball-sealer in-stage diversion under the effect of heterogeneous stress field in a horizontal well[J]. Natural Gas Industry, 2020, 40(3): 82–91.
[25] 达引朋,李建辉,王飞,等. 长庆油田特低渗透油藏中高含水井调堵压裂技术[J]. 石油钻探技术,2022,50(3):74–79. DA Yinpeng, LI Jianhui, WANG Fei, et al. Plugging and fracturing technology for high water cut wells in ultra-low permeability reservoirs of Changqing Oilfield[J]. Petroleum Drilling Techniques, 2022, 50(3): 74–79.
[26] CHENG Wan, LU Chunhua, FENG Guanxiong, et al. Ball sealer tracking and seating of temporary plugging fracturing technology in the perforated casing of a horizontal well[J]. Energy Exploration & Exploitation, 2021, 39(6): 2045–2061.
[27] OOKAWARA S, AGRAWAL M, STREET D, et al. Quasi-direct numerical simulation of lift force-induced particle separation in a curved microchannel by use of a macroscopic particle model[J]. Chemical Engineering Science, 2007, 62(9):2454-2465.
[28] SORIA J, GAUTHIER D, FLAMANt G, et al. Coupling scales for modelling heavy metal vaporization from municipal solid waste incineration in a fluid bed by CFD[J]. Waste Management, 2015, 43(9):176-187.
[29] 吴宏杰,肖博,张旭东. 页岩气井暂堵重复压裂工艺技术研究及应用[J]. 石油化工应用,2020,39(9):53–56. WU Hongjie, XIAO Bo, ZHANG Xudong. Research and application of temporary plugging and re-fracturing technology for shale gas wells[J]. Petrochemical Application, 2020, 39(9): 53–56.
[30] 吕瑞华,刘奔,安琳. 水平井转向压裂用暂堵球运移封堵规律研究[J]. 石油机械,2020,48(7):117–122. LYU Ruihua, LIU Ben, AN Lin. Study on the migration and plugging Laws of temporary plugging ball for divert fracturing in horizontal wells[J]. China Petroleum Machinery, 2020, 48(7): 117–122.
[31] 廖仕孟,桑宇,宋毅,等. 页岩气水平井套管变形影响段分段压裂工艺研究及现场试验[J]. 天然气工业,2017,37(7):40–45. LIAO Shimeng, SANG Yu, SONG Yi, et al. Research and field-tests of staged fracturing technology for casing deformation section in horizontal shale gas wells[J]. Natural Gas Industry, 2017, 37(7): 40–45.
[32] 卢修峰,刘凤琴. 投球分压的理论验证及实例分析[J]. 石油钻采工艺,1994,16(3):57–62. doi: 10.13639/j.odpt.1994.03.014 LU Xiufeng, LIU Fengqin. The theory verification and examples analysis of steering ball separate-layer fracturing[J]. Oil Drilling & Production Technology, 1994, 16(3): 57–62. doi: 10.13639/j.odpt.1994.03.014
-
期刊类型引用(5)
1. 李绍鹏，李常兴，周鹏，蓝宝锋，蔡灿，钟涛. 页岩气水平井暂堵坐封机制与可控暂堵压裂工艺. 断块油气田. 2024(03): 432-438 . 
百度学术
2. 何乐，朱炬辉，梁兴，赵智勇，管彬，安树杰. 基于管外光纤监测的页岩气水平井多簇压裂效果评价. 石油钻探技术. 2024(04): 110-117 . 本站查看
3. 王雷，叶荣俊，陈德瑞，许文俊，张健鹏. 超深高温高盐油藏膨胀乳液调驱技术研究与应用. 特种油气藏. 2024(06): 130-136 . 百度学术
4. 李永明，马健，栗铁峰，孙鹏. 页岩水平井分段多簇缝口暂堵参数优化——以川南下寒武统筇竹寺组页岩为例. 西南石油大学学报(自然科学版). 2024(06): 137-145 . 百度学术
5. 刘罗云，李扬，王迪. 水平井筒暂堵球运移规律实验及效果评价. 东北石油大学学报. 2023(06): 55-66+128-129 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 193
- HTML全文浏览量: 47
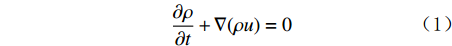
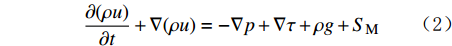
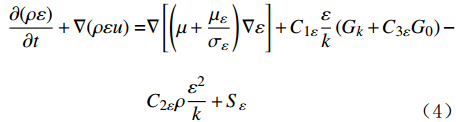
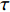
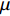
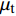
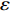
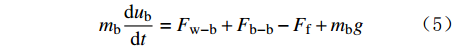
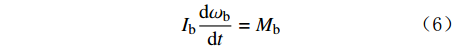
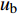
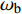
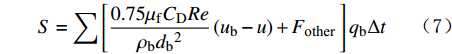
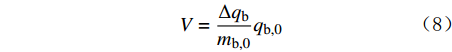
- PDF下载量: 74
- 被引次数: 5
