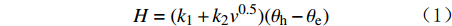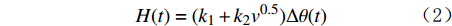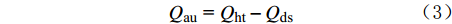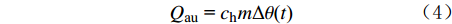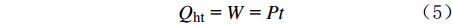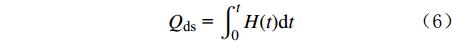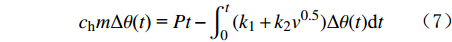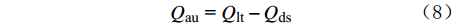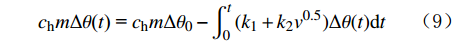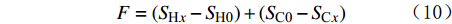Downhole Flow Rate Measurement Method Based on the Time Domain Integral of Heat Conduction
-
摘要:
针对油田低产液生产井流量测量困难的问题,根据多相流体热力学理论,利用整个测量周期内探测器周围流体冲刷引起的热传导效应,提出了一种基于热传导时域积分的井下流量测量方法。首先,采用间歇式恒功率加热的方式,给探测器提供周期性能量;然后,采用积分法计算和分析了探测器内部温度在升温和降温过程中随外界流体流量变化的规律。理论分析与试验结果表明,时域积分面积与流量呈极好的相关性,尤其在低流量条件下具有较高的分辨率,该方法解决了传统涡轮流量计在流量较低情况下因涡轮无法启动导致失去检测能力的问题。基于热传导时域积分的井下流量测量方法,促进了油水两相流检测技术的发展,为低产液井流量测量提供了一种新的技术手段。
Abstract:In light of the difficulties in measuring the flow rate of low-productivity producers in oil fields, the heat conduction effect caused by ambient fluid around the detector in the whole measurement cycle was adopted, a downhole flow rate measurement method based on time domain integral of heat transfer was put forward according to multiphase fluid thermodynamic theory. First, intermittent constant power heating was used to provide periodic energy to the detector. Then, an integral method was employed to calculate and analyze the variation of the internal temperature variation law of the detector with the external fluid flow during heating and cooling. The theoretical analysis and experimental study showed that the time domain integral area had an excellent correlation with the flow rate, and had high resolution under low flow rate condition. The problem that traditional turbine flowmeters lose their capability of detection as their turbines couldn’t be activated under low flow rate was solved with this method. The downhole flow rate measurement method based on the time domain integral of heat conduction has promoted the development of oil-water two-phase flow detection technology. It has provided a new technical means for flow rate measurement of low-productivity producers.
-
随着油气田勘探开发的不断深入,我国大部分油田都进入到开发中后期,高含水、低产液是其主要特点[1-3]。受启动排量的限制,常规的涡轮流量计在低流量条件下无法工作,目前绝大多数井下流量计都不能很好地解决低流量检测难题[4-8]。热式流量计是近年来发展较快的一类流量计,它是建立在热传导理论的基础上,利用流体和外部加热源之间热量交换的关系来测量流体流量,可以在低流速下获得更高的测量精度。热式流量计具有结构简单、复用性强、压力损失小、无可动部件、稳定性强、可靠性高和测量范围广等优势,特别适用于低产液油井微小流量测量[9-10]。
目前,热式流量检测方法的研究主要集中在恒功率式和恒温差式2种控制算法的优化方面[11-13]。其中,恒功率式是以恒定功率给测速探测器加热,通过测量测速探测器与流体环境的温差来计算流量,具有测量范围大、设计结构简单等特点,但对于极低流量的测量,由于测速探测器强迫对流换热减小,恒定的加热功率会在测速探测器周围产生梯度很大的温度场,不适合阵列化检测[14]。恒温差式是通过保持测速探测器与流体环境温差恒定,通过测量加热功率的变化来计算流量[15-18],具有响应速度快、低流量测量精度高等特点,但是受测速探测器热惯性及滞后效应的影响,其建立稳定恒温差温度场的速度较慢,且易受环境温度波动的影响,造成测量结果不稳定[19-20]。针对上述问题,笔者提出了一种基于热传导时域积分的流量测量方法,其优势在于充分利用测速探测器在整个测量周期内与周围流体之间的强迫对流换热关系,极大地提高了井下流量测量的精确度和稳定性。
1. 热式流量测量基本原理
热式流量测量系统采用双探测器结构,其中一个为测温探测器,由温度传感器和密闭腔体组成,放置在流体的上游,用来测量流体环境温度;另一个为测速探测器,由加热器、温度传感器和密闭腔体组成,放置在流体的下游,用来测量流体的流速(见图1)。测量时2个探测器浸入流体中,二者间隔一定距离。
测量过程中给测速探测器内部加热器供电使其产生热量,根据传热学原理,在热平衡状态下测速探测器与周围流体的对流换热关系为[21]:
H=(k1+k2v0.5)(θh−θe) (1) 式中:H为换热功率(表示测速探测器与流体之间换热的快慢),W;v为被测流体的流速,m/s;θh为测速探测器的温度,℃;θe为测温探测器的温度(即流体所在环境的温度),℃;k1和k2为被测流体各物性参数的统一参量。
在压力不变的条件下,对于给定的探测器和恒定温度的被测流体,k1和k2反映此时被测流体的导热率、普朗特数等物性参数的综合计算结果,可视为常量。由式(1)可见,在流体物性参数k1和k2恒定的条件下,换热功率与流体流速之间有明确的解析关系,通过测量测速探测器与周围流体之间换热的快慢,即可估算出被测流体的流速;若管道的横截面积已知,可进一步计算流体的流量。
2. 系统工作时序与温度变化规律
测速探测器采用周期性间歇式恒功率加热的工作模式。系统一个工作周期开始时,测速探测器内部的加热器开始加热,当测速探测器的温度达到系统设定的阈值温度θth时,加热器停止加热,直至该工作周期结束。随着测速探测器内加热器周期性加热,测速探测器温度也会呈现周期性变化,其工作流程如图2所示。
具体工作流程为:1)利用外部控制电路给测速探测器内部加热器提供5 V工作电压使其产生热量(见图2(a)中红色加热区域),供电始于t1时刻;2)加热器产生的热量会通过测速探测器外壁向周围流体扩散,同时引起测速探测器的温度升高,升温始于t1时刻;3)测速探测器设置一个阈值温度θth,当检测到测速探测器的温度达到阈值温度θth时,停止为测速探测器内部的加热器供电,该时刻记为t2。测速探测器的升温曲线如图2(b)中t1至t2段所示,记为升温阶段tup;4)根据热惯性效应,测速探测器的温度达到阈值温度θth后还会再升高一段时间,随后温度会缓慢降低至阈值温度θth,此时刻记为t3,图2(b)中t2至t3曲线段记为跨越阶段tcross;5)在没有热量补充的前提下,周围流体的流动会带走测速探测器内部剩余的热量,测速探测器进入降温阶段,假设在t4时刻测速探测器温度降低至与环境温度持平,t3至t4曲线段记为降温阶段tdown;6)为了确保下一次加热之前测速探测器内部的温度与环境温度保持一致,加热器继续保持断电状态,此阶段测速探测器内部与外部流体之间几乎没有温度差,t4至t5曲线段记为温度保持阶段tkeep。
测速探测器内部的加热器按照图2(a)中的时序工作时,测速探测器的温度会按照图2(b)中的曲线在tup、tcross、tdown和tkeep等4个阶段轮流往复。因此,进一步分析测速探测器温度曲线的变化规律,有助于提出更加合理的检测方案。
3. 测速探测器加热及冷却过程分析与数值模拟
3.1 测速探测器加热过程
将测速探测器浸入到流体中,在初始状态下,测速探测器与流体环境温度相同,二者温差为零,因此二者之间的热量传递也几乎为零。若从某一时刻起,给测速探测器内部的加热器提供恒定功率的电能使其产生热量,随着测速探测器温度升高,热量会通过测速探测器外壁向周围流体扩散。因此,测速探测器与周围流体之间的温差及二者之间的换热功率都是随加热时间t变化的量,分别记为Δθ(t)和H(t)。因此,式(1)可改写为:
H(t)=(k1+k2v0.5)Δθ(t) (2) 式中,Δθ(t)为测速探测器与流体环境的温差,也可视为测速探测器升高的温度,℃。
根据热平衡原理,可得:
Qau = Qht−Qds (3) 式中:Qht为测速探测器内部的加热器产生的热量,J;Qau为测速探测器当前累积的热量,J;Qds为测速探测器向流体耗散的热量,J。
测速探测器增加的热量Qau可通过自身温度的变化反映出来,其关系式为:
Qau = chmΔθ(t) (4) 式中:ch为测速探测器平均比热容,J/(kg·℃);m为测速探测器的质量,kg。
加热器产生的热量Qht等于系统对加热器提供的电能,所以有:
Qht = W = Pt (5) 式中:W为加热器消耗的电能,J;P为加热器加热时的电功率,W。
测速探测器耗散的热量是一个与时间有关的积分表达式,升温过程中,测速探测器向周围流体传导的热量为:
Qds = ∫t0H(t)dt (6) 综合式(2)—式(5),可得出测速探测器与流体温差Δθ(t)与时间t的关系式:
chmΔθ(t) = Pt−∫t0(k1+k2v0.5)Δθ(t)dt (7) 为了分析测速探测器在不同流量条件下以恒定功率加热过程中的温度变化规律,利用Matlab进行数值模拟。设流体管道的直径为124 mm,测速探测器的直径为5 mm,长度为30 mm,测试流体为纯水,加热器的加热功率为1.25 W,将测速探测器和被测流体相关参数代入式(7),得到不同流量条件下恒功率加热过程中测速探测器与流体环境温差的变化曲线,见图3。
从图3(a)可以看出,随着加热器持续加热,测速探测器与环境温度之间的温差会逐渐增大至恒定值,此时加热功率等于散热功率,处于热平衡状态。图3(b)为图3(a)的局部放大图,可以看出,流量越小,测速探测器温度升高的速度越快,反之亦然。若设置一个阈值温度θth(例如1.0 ℃),在加热功率恒定的前提下,流量越小,达到阈值温度的时间越短;流量越大,达到阈值温度的时间越长。
3.2 测速探测器冷却过程
经过一段时间的恒功率加热后,测速探测器的内部会有热量累积而导致温度升高。停止加热后测速探测器累积的热量会以热传导的方式逐渐耗散到流体中,直至测速探测器与流体之间的温差为零。假设加热停止时,测速探测器剩余的热量为Qlt,探测器与流体之间的温差为Δθ0,根据热平衡原理可得:
Qau = Qlt−Qds (8) 综合式(4)、式(6)和式(8),可得:
chmΔθ(t) = chmΔθ0−∫t0(k1+k2v0.5)Δθ(t)dt (9) 假定Δθ0=1.0 ℃,利用Matlab进行数值模拟,得到不同流量条件下测速探测器冷却过程中的温度变化曲线,见图4。
从图4(a)可以看出:测速探测器中的加热器停止加热后,受到周围流体的冲刷,测速探测器内部的热量随之不断扩散到流体中,测速探测器与流体之间的温差会逐渐减小至零;流体的流速越大,测速探测器温度降低的速度就越快。图4(b)为图4(a)的局部放大图,可以看出:在测速探测器与流体之间的温差不等于零之前,流体的流量越大,单位时间内测速探测器内部温度下降得就越快,其温度就越低;反之,流体的流量越小,测速探测器内部温度下降得就越慢,其温度也越高。
3.3 全域过程分析
通过前面对测速探测器在加热及冷却过程中温度变化曲线的数值模拟和试验验证,得到不同流量条件下测速探测器一个工作周期的温度变化曲线,如图5所示。
从图5可以看出:小流量条件下,测速探测器温度升高的速度快,从环境温度升至阈值温度所需时间短,而温度降低的速度缓慢;大流量条件下,测速探测器温度升高的速度缓慢,从环境温度升至阈值温度所需时间较长,而温度降低的速度较快。因此,测速探测器的温度变化曲线隐含着流体流量信息,合理利用测速探测器温度变化的规律,可为流体的流量提供有效测量方法。
4. 基于时域积分的流量检测方法
进一步分析图5中测速探测器内部温度曲线的变化规律,假设环境温度为θe,阈值温度为θth,将升温曲线与直线x=t2和直线y=θe围成的封闭区域视为加热区域,其面积称作加热面积,记为SH,如图6(a)所示;跨越曲线及降温曲线与x=t2、x=t4和y=θe围成的封闭区域视为冷却区域,其面积称作冷却面积,记为SC,如图6(b)所示。显然,加热面积和冷却面积随流量变化而变化。当流体的流量最小时(例如0 m3/d),由于流体处于静止,根据传热学原理,测速探测器热量被带走的速度最慢,此时探测器内部温度上升速度最快,加热面积SH最小,记为SH0,而温度降低速度最慢,冷却面积SC最大,记为SC0;当流体处于流动状态时,流量越大,热量被带走的就越多。因此,加热面积随着流量增大呈单调递增,冷却面积随着流量增大呈单调递减。
流量为0 m3/d时,加热面积SH0如图7(a)所示,冷却面积SC0如图7(b)所示。若当前被测流体的加热面积和冷却面积已知,分别记为SHx和SCx(见图7(c)和7(d))。为了更好地反映冷热面积变化特征与流量之间的单调递增关系,引入了一个参数流量相关量F(无量纲),F与面积的关系记为:
F=(SHx−SH0)+(SC0−SCx) (10) 式(10)表明:被测流体流量为0 m3/d时,SHx =SH0,SCx =SC0,此时F=0;随着流量增大,SHx逐渐增大,SCx逐渐减小,因为二者此消彼长,所以F值也随之增大,与流量呈单调递增关系,符合一般测量规律。
5. 检测系统设计
根据实际测量需要,设计了检测系统硬件结构,主要由温度传感器、A/D转换模块、加热器、加热驱动模块、采集控制器和CAN通信模块组成(见图8)。A/D转换模块可以实时采集测温探测器和测速探测器中温度传感器的温度模拟信号,并转换为温度数字信号传送给采集控制器;采集控制器根据系统工作时序,通过加热驱动模块来控制测速探测器中的加热器。同时,采集控制器将温度数据和面积计算结果通过CAN通信模块传送至井下遥传短节。
根据检测系统硬件结构,设计并制作了流量检测电路板,包括逻辑控制板和加热驱动板。逻辑控制板的主要功能是系统工作时序控制、探测器温度采集及与井下遥传短节设备之间通信;加热驱动板的主要功能是根据系统控制时序为加热器提供间断恒功率的电能。2块电路板独立设计,能够将数字电路与模拟电路分隔开,避免模块之间相互干扰。此外,2块电路板平行对齐安装在仪器平板骨架两侧,较好地解决了空间占用和散热的问题。
6. 试验与数据分析
为了验证测量方法的可行性,搭建了流量测试试验平台,主要由水箱、水泵、标准流量计、模拟井筒、测温探测器、测速探测器、流量检测电路、CAN分析仪及计算机等部分组成(见图9)。试验时,以自来水为试验流体,试验流体在水泵的驱动下在水箱和模拟井筒中循环流动,通过调节水泵的转速,可以模拟井筒内流量为0~30 m3/d的测试条件。
通过调节水泵的转速调整流量,流量间隔为6 m3/d,流量依次设置为0,6,12,18,24和30 m3/d,采集不同流量下一个工作周期中测速探测器与测温探测器之间的温差变化,结果如图10所示(图10中,红色曲线为测速探测器开始加热直至温度升高到设定阈值温度的过程,为探测器升温阶段tup,其积分面积视为加热面积SH;蓝色曲线为测速探测器温度超过阈值温度直至温度降低至工作周期结束的过程,为探测器跨越阶段tcross和降温阶段tdown的组合,其积分面积视为冷却面积SC)。系统的工作周期为60 s,温度采样间隔为0.5 s,因此一个工作周期的采样数量为120个。
从图10可以看出,随着流量增大,峰值温度、到达阈值温度的时刻、加热面积与冷却面积等方面均发生了变化,具体表现在:1)无流体流动的条件下,阈值温度到达时刻约在采样点序号16处,随着流量增大,阈值温度到达时刻的序号后移,例如在流量为6~30 m3/d时,阈值温度到达时刻的序号分别为23,24,24,25和25。这表明阈值温度到达时刻与低流量存在一定的单调相关性,但随着流量增大,这种关系逐渐减弱。2)峰值温度随着流量增大呈单调递减规律,但这一规律并不明显,例如流量分别为12和18 m3/d时的峰值温度分别为12 994和12 665,二者相差很小。因此,利用峰值温度来测量流量不能获得良好的分辨率。3)采用时域分段积分的方法计算曲线的加热面积和冷却面积,可见加热面积与流量呈单调递增趋势,冷却面积与流量呈单调递减趋势(见图10(a)—图10(e)右上角图例中数值)。这表明,时域分段积分法可以从曲线的微小变化趋势中提取流量信息,能够充分利用探测器在加热和冷却过程中与周围流体的强迫对流热交换效应,较好地解决了低流量测量的难题。
为了进一步测试热传导时域积分法的有效性和分辨率,在0~30 m3/d范围内按照2 m3/d间隔进行流量试验,每个流量条件下重复3次,每次连续采集20个样本,得到不同流量条件下系统计算的F平均值及其误差(见表1)。根据表1中的试验数据,绘制得到F与实际流量的关系曲线及误差波动范围,如图11所示。
表 1 系统流量测量结果分析Table 1. Measurement results analysis of system flow rate流量/
(m3·d−1)F平均值 F正向绝对误差 F正向相对误差,% F负向绝对误差 F负向相对误差,% 0 0 2 346 3 807 2 150 310 1 573 1.047 3 084 2.052 4 247 043 1 928 0.780 2 873 1.163 6 289 253 2 156 0.745 1 492 0.516 8 303 119 3 194 1.054 1 787 0.590 10 315 152 3 223 1.023 2 895 0.919 12 325 878 2 438 0.748 2 336 0.717 14 334 152 2 175 0.651 1 650 0.494 16 343 104 1 258 0.367 2 644 0.771 18 351 104 2 246 0.640 2 035 0.580 20 358 761 2 044 0.570 1 359 0.379 22 365 920 1 596 0.436 1 979 0.541 24 371 161 1 761 0.474 2 202 0.593 26 376 053 2 040 0.542 2 107 0.560 28 380 279 2 194 0.577 1 317 0.346 30 384 999 1 275 0.331 1 928 0.501 从图11可以看出:F值与流量之间呈良好的单调递增关系,0~6 m3/d超低流量区间的曲线斜率较大,6~30 m3/d流量区间二者近似呈线性关系,这与理论分析基本一致;系统测量误差在−2.05%~1.05%范围内波动,说明系统测量误差较小,重复性极好;从分辨率角度看,单位流量系统正负向误差的平均值约为2 500,考虑流体湍流、探测器倾斜等不利因素和系统的冗余量,合理假设系统单位流量的最小分辨单位为平均误差的2倍,约为5 000,则根据曲线的斜率可以计算得到,系统在0~6 m3/d超低流量区间的分辨率可达0.5 m3/d;随着流量增大(6~30 m3/d),系统的灵敏度会有所降低,但分辨率仍然能够达到1.0 m3/d。
7. 结论与建议
1)从信号与系统的角度研究流量探测器在加热和冷却阶段内部温度变化特性与周围流体流速之间的变化关系,建立了热传导时域积分特性与流量之间的数学模型,针对传统恒功率和恒温差热式流量计在井下流量测量中的不足,提出了基于热传导时域积分的井下流量测量方法。
2)试验研究结果表明,该方法能够稳定有效地检测流体的流量,在0~6 m3/d超低流量条件下的分辨率可达0.5 m3/d,在6~30 m3/d流量条件下的分辨率为1.0 m3/d。
3)测量过程中阈值温度的设置极为关键,若阈值温度设置过高,会导致测速探测器产生热量累积,从而引起系统测量误差;若阈值温度设置过低,会导致测速探测器温度变化幅度小,从而引起系统分辨率降低。因此,阈值温度是下一阶段研究的问题之一。
-
表 1 系统流量测量结果分析
Table 1 Measurement results analysis of system flow rate
流量/
(m3·d−1)F平均值 F正向绝对误差 F正向相对误差,% F负向绝对误差 F负向相对误差,% 0 0 2 346 3 807 2 150 310 1 573 1.047 3 084 2.052 4 247 043 1 928 0.780 2 873 1.163 6 289 253 2 156 0.745 1 492 0.516 8 303 119 3 194 1.054 1 787 0.590 10 315 152 3 223 1.023 2 895 0.919 12 325 878 2 438 0.748 2 336 0.717 14 334 152 2 175 0.651 1 650 0.494 16 343 104 1 258 0.367 2 644 0.771 18 351 104 2 246 0.640 2 035 0.580 20 358 761 2 044 0.570 1 359 0.379 22 365 920 1 596 0.436 1 979 0.541 24 371 161 1 761 0.474 2 202 0.593 26 376 053 2 040 0.542 2 107 0.560 28 380 279 2 194 0.577 1 317 0.346 30 384 999 1 275 0.331 1 928 0.501 -
[1] AMINA B, AHMED H. An overview of thermal mass flowmeters applicability in oil and gas industry[J]. Energy Procedia, 2017, 141: 299–303. doi: 10.1016/j.egypro.2017.11.109
[2] 李群生,朱礼平,李果,等. 基于井下流量测量的微流量控制系统[J]. 石油钻探技术,2012,40(3):23–27. doi: 10.3969/j.issn.1001-0890.2012.03.005 LI Qunsheng, ZHU Liping, LI Guo, et al. Micro-flow control system based on downhole flow measurement[J]. Petroleum Drilling Techniques, 2012, 40(3): 23–27. doi: 10.3969/j.issn.1001-0890.2012.03.005
[3] 王江帅,李军,柳贡慧,等. 气侵条件下新型双梯度钻井环空出口流量变化规律研究[J]. 石油钻探技术,2020,48(4):43–49. doi: 10.11911/syztjs.2020043 WANG Jiangshuai, LI Jun, LIU Gonghui, et al. Study on the change law of annular outlet flow rate in new-type dual-gradient drilling under gas cut condition[J]. Petroleum Drilling Techniques, 2020, 48(4): 43–49. doi: 10.11911/syztjs.2020043
[4] 杨玲智,周志平,杨海恩,等. 桥式同心井下恒流分层注水技术[J]. 石油钻探技术,2022,50(4):104–108. doi: 10.11911/syztjs.2022051 YANG Lingzhi, ZHOU Zhiping, YANG Haien, et al. Downhole constant-flow stratified water injection technology with concentric bridge[J]. Petroleum Drilling Techniques, 2022, 50(4): 104–108. doi: 10.11911/syztjs.2022051
[5] 王鲁海,李军,关松,等. 低流量条件下涡轮流量计的黏度响应特性[J]. 测井技术,2012,36(4):336–339. doi: 10.3969/j.issn.1004-1338.2012.04.002 WANG Luhai, LI Jun, GUAN Song, et al. The performance of turbine flowmeter with viscosity changes under low flow condition[J]. Well Logging Technology, 2012, 36(4): 336–339. doi: 10.3969/j.issn.1004-1338.2012.04.002
[6] 王月明,贾华,李文涛,等. 管道对电磁流量计敏感场影响研究[J]. 仪表技术与传感器,2017(7):29–31. doi: 10.3969/j.issn.1002-1841.2017.07.009 WANG Yueming, JIA Hua, LI Wentao, et al. Influence study of pipelines on electromagnetic flow meter sensitive field[J]. Instrument Technique and Sensor, 2017(7): 29–31. doi: 10.3969/j.issn.1002-1841.2017.07.009
[7] 张易农,彭静,程耀华,等. 多种超声流量计对气液两相流流量计量的试验研究[J]. 中国测试,2017,43(9):143–147. doi: 10.11857/j.issn.1674-5124.2017.09.026 ZHANG Yinong, PENG Jing, CHENG Yaohua, et al. Experimental study on gas-liquid two-phase flow measurement by using multiple ultrasonic flowmeter[J]. China Measurement & Testing Technology, 2017, 43(9): 143–147. doi: 10.11857/j.issn.1674-5124.2017.09.026
[8] 张德政,王志彬,于志刚,等. 高液气比气井临界携液流量计算方法[J]. 断块油气田,2022,29(3):411–416. ZHANG Dezheng, WANG Zhibin, YU Zhigang, et al. Calculation method of critical liquid-carrying flow rate of high liquid-gas ratio gas well[J]. Fault-Block Oil & Gas Field, 2022, 29(3): 411–416.
[9] KIM T H, KIM D K, KIM S J. Study of the sensitivity of a thermal flow sensor[J]. International Journal of Heat and Mass Transfer, 2009, 52(7/8): 2140–2144.
[10] BEKRAOUI A, HADJADJ A. Thermal flow sensor used for thermal mass flowmeter[J]. Microelectronics Journal, 2020, 103: 104871. doi: 10.1016/j.mejo.2020.104871
[11] 姜兆宇. 热式质量流量计应用于井下液相流量测量研究[D]. 大庆: 东北石油大学, 2013. JIANG Zhaoyu. The research of thermal mass flowmeter applied to downhole liquid flow rate measurment[D]. Daqing: Northeast Petroleum University, 2013.
[12] 汪栋良,余厚全,杨旭辉,等. 井下恒功率热式流量计设计与实现[J]. 石油管材与仪器,2018,4(2):20–23. doi: 10.19459/j.cnki.61-1500/te.2018.02.006 WANG Dongliang, YU Houquan, YANG Xuhui, et al. Design and implementation of downhole constant power thermal flowmeter[J]. Petroleum Tubular Goods & Instruments, 2018, 4(2): 20–23. doi: 10.19459/j.cnki.61-1500/te.2018.02.006
[13] 马杰. 基于恒功率原理的核电级热式质量流量计研制[D]. 合肥: 合肥工业大学, 2021. MA Jie. Development of nuclear thermal mass flowmeter based on constant power principle[D]. Hefei: Hefei University of Technology, 2021.
[14] 范宋杰,魏勇,余厚全,等. 阵列恒温差热式流量计的设计与开发[J]. 科学技术与工程,2021,21(18):7513–7518. doi: 10.3969/j.issn.1671-1815.2021.18.016 FAN Songjie, WEI Yong, YU Houquan, et al. Design and development of a constant temperature differential thermal flowmeter with sensor array[J]. Science Technology and Engineering, 2021, 21(18): 7513–7518. doi: 10.3969/j.issn.1671-1815.2021.18.016
[15] 张夷非,魏勇,余厚全,等. 恒温差热式流量计影响因素模拟与试验研究[J]. 石油钻探技术,2021,49(2):121–126. doi: 10.11911/syztjs.2021023 ZHANG Yifei, WEI Yong, YU Houquan, et al. Simulation and experimental studies on the influencing factors of a thermal flowmeter with constant temperature difference[J]. Petroleum Drilling Techniques, 2021, 49(2): 121–126. doi: 10.11911/syztjs.2021023
[16] 汪余景,翟军勇. 基于恒温差的热式空气流量计[J]. 仪表技术与传感器,2017(6):41–43. doi: 10.3969/j.issn.1002-1841.2017.06.011 WANG Yujing, ZHAI Junyong. Thermal air flow meter based on constant temperature difference[J]. Instrument Technique and Sensor, 2017(6): 41–43. doi: 10.3969/j.issn.1002-1841.2017.06.011
[17] JIANG Junhao, CAO Shaozhong. The design of novel thermal gas mass flowmeter[J]. Applied Mechanics and Materials, 2012, 224: 435–439. doi: 10.4028/www.scientific.net/AMM.224.435
[18] 戴卓勋. 基于热传导的恒温差式低产液量检测仪研制[D]. 西安: 西安石油大学, 2021. DAI Zhuoxun. Development of low liquid yield detector with constant temperature difference based on heat conduction[D]. Xi’an: Xi’an Shiyou University, 2021.
[19] 贾惠芹,戴卓勋,陈强,等. 井下恒温差热式液体流量计[J]. 石油钻采工艺,2021,43(6):817–822. doi: 10.13639/j.odpt.2021.06.020 JIA Huiqin, DAI Zhuoxun, CHEN Qiang, et al. Downhole constant temperature difference thermal liquid flowmeter[J]. Oil Drilling & Production Technology, 2021, 43(6): 817–822. doi: 10.13639/j.odpt.2021.06.020
[20] 蔡晖,刘英宪,马奎前,等. 海上油藏流场评价方法[J]. 特种油气藏,2021,28(4):129–135. doi: 10.3969/j.issn.1006-6535.2021.04.018 CAI Hui, LIU Yingxian, MA Kuiqian, et al. Study on evaluation method of flow field in offshore oil reservoirs[J]. Special Oil & Gas Reservoirs, 2021, 28(4): 129–135. doi: 10.3969/j.issn.1006-6535.2021.04.018
[21] 张夷非,魏勇,余厚全,等. 恒温差热式流量计分段PID控制的仿真与实验[J]. 测井技术,2021,45(3):284–289. doi: 10.16489/j.issn.1004-1338.2021.03.010 ZHANG Yifei, WEI Yong, YU Houquan, et al. Simulation and experimental research on segmented PID control of constant temperature differential thermal flowmeter[J]. Well Logging Technology, 2021, 45(3): 284–289. doi: 10.16489/j.issn.1004-1338.2021.03.010
-
期刊类型引用(2)
1. 孙虎,郭阳,张媛,喻建胜,陈思锦. 智能化钻井完井技术研究与工程实践. 钻采工艺. 2025(01): 46-54 .  百度学术
百度学术
2. 廖华林,屈峰涛,许玉强,魏凯. 复合模型与模糊推理联合的溢流风险分级评估新方法. 天然气工业. 2025(03): 140-151 .  百度学术
百度学术
其他类型引用(0)




 下载:
下载: