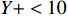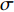Optimization Design and Numerical Analysis of Flow Passage Converters in LWD Tools
-
摘要: 随钻测井仪流道转换器流道截面设计不合理,不仅会造成随钻测井仪器内流道局部流场紊乱,致使仪器局部冲刷严重,造成仪器使用寿命缩短;还会导致仪器压力损失偏高,影响仪器的适用性。为此,采用CFD方法,对某型随钻测井仪流道转换器进行优化设计,并对4种设计方案进行了全三维数值模拟和对比,认为影响流道转换器流场性能的主要因素是扩张角和内流道截面积的连续性。最优设计方案的扩张角较小,内流道截面积连续,轴向速度下降更平缓,总压损失最小,流场流速分布更均匀。试验结果表明,流道转换器扩张角、内流道截面积不连续性与流道转换器流场分布均匀性呈负相关,与压力损失呈正相关;总压损失系数理论值与试验值对应的差值不大于0.076%,且变化趋势均与理论分析结果相同。研究结果为流道转换器的优化设计提供了理论依据。Abstract: Improper design of flow passage converter section in LWD ( logging while drilling) tools can cause local flow-field turbulence and result in serious local erosion of the tool, thus reducing its service life. It can also lead to large pressure loss of the tool and affect its applicability. For this reason, CFD (computational fluid dynamics) method was applied for the optimization design of a certain type of flow passage converter in an LWD tool. According to the full 3D numerical simulation and comparison of four design schemes, the main factors affecting the flow-field performance of the flow passage converter were thought to be the expansion angle and the continuity of the cross-sectional area of the internal flow passage. The optimal design has a smaller expansion angle, a more continuous cross-sectional area of the internal flow passage, a gentler decline in axial velocity, a minimum total pressure loss, and a more uniform flow velocity distribution in the flow field. The research results showed that the expansion angle and the discontinuity of the cross-sectional area of the internal flow passage were negatively associated with the uniformity of the flow field distribution in the flow passage converter and positively with the pressure loss. The difference between theoretical and experimental total pressure loss coefficients was not more than 0.076%, and the change trend was the same as the result of theoretical analysis. The research results can effectively serve as a theoretical basis for the optimization design of flow passage converters.
-
Keywords:
- LWD tool /
- flow passage converter /
- optimization design /
- numerical simulation
-
随着测井技术迅速发展[1-2],国内外目前已研究形成了随钻方位电阻率测井仪、随钻中子测井仪、随钻密度测井仪、随钻声波测井仪、随钻电磁波测井仪和随钻电成像测井仪等一系列测井仪器,并在各大油田广泛应用[3-8]。随钻测井仪通常由钻铤、电路骨架和流道转换器等部件组成。井下作业时,将不同种类的随钻测井仪串联,每支随钻测井仪一般需装配2个流道转换器,流道转换器的作用是将中心(环空)流道转换成环空(中心)流道,使用数量较多,是随钻测井仪的常用部件,也是关键部件之一。若流道转换器内流道截面设计不当,不仅会造成随钻测井仪内流道局部流场紊乱,使仪器局部冲刷严重,造成仪器使用寿命缩短;还会导致仪器压力损失偏高,影响仪器的适用性[9-10]。
目前,国内外鲜见采用数值计算分析方法对流道转换器进行内流道设计优劣对比的研究。笔者采用计算流体力学(computational fluid dynamics,简称CFD)方法,对某型随钻测井仪流道转换器设计方案进行了全三维数值模拟[11-13],对比分析了影响内流道流场设计的关键因素,研究结果为流道转换器的优化设计提供了理论依据。
1. 控制方程
流体的运动可以用质量、动量和能量守恒定律来描述,并采用方程组的形式来表述。对于理想的黏性流体,此方程组称为Navier-Stokes方程组[14]。其中,质量守恒定律描述动力学特性,在流体系统内部没有新质量源的情况下,该系统质量的变化等于通过系统边界的质量流量。因此,质量守恒方程也称为连续方程,可以表示为:
\frac{{\partial \rho }}{{\partial t}} + {\bf{\nabla}} \cdot \left( {\rho {\boldsymbol{v}}} \right) = 0 (1) 式中:
\rho 为密度,{\rm{kg}}/{{\rm{m}}^3} ;t为时间,s;{\boldsymbol{v}} 为速度,m/s;{\bf{\nabla}} 为散度算子。动量守恒方程表明,流体系统的动量对时间的变化率等于外界作用在系统上的外力矢量和。在笛卡尔坐标系下,动量守恒方程在
x,y,z 方向的分量为:\frac{{\partial \left( {\rho {v_x}} \right)}}{{\partial t}} + {\bf{\nabla}} \cdot \left( {\rho {v_x}{\boldsymbol{v}}} \right) = - \frac{{\partial P}}{{\partial x}} + \frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}} + {F_x} (2) \frac{{\partial \left( {\rho {v_y}} \right)}}{{\partial t}} + {\bf{\nabla}} \cdot \left( {\rho {v_y}{\boldsymbol{v}}} \right) = - \frac{{\partial P}}{{\partial y}} + \frac{{\partial {\tau _{xy}}}}{{\partial x}} + \frac{{\partial {\tau _{yy}}}}{{\partial y}} + \frac{{\partial {\tau _{zy}}}}{{\partial z}} + {F_y} (3) \frac{{\partial \left( {\rho {v_z}} \right)}}{{\partial t}} + {\bf{\nabla}} \cdot \left( {\rho {v_z}{\boldsymbol{v}}} \right) = - \frac{{\partial P}}{{\partial z}} + \frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}} + {F_z} (4) 式中:P为压力,N;
{\tau _{ii}}\left( {i = x,y,z} \right) 为黏性力张量{\boldsymbol{\tau}} 在各个方向的分量,N;{F_i}\left( {i = x,y,z} \right) 为彻体力{\boldsymbol{F}} 在各个方向的分量,N;{v_i}(i = x,y,z) 为速度{\boldsymbol{v}} 在各个方向的分量,m/s。能量守恒定律在热力学上又称为热力学第一定律。该定律表明流体系统能量的变化等于作用在该系统上的力所作的功与传递到系统内的热量之和。因此,能量守恒方程可以表示为:
\frac{{\partial \left( {\rho E} \right)}}{{\partial t}} + {\bf{\nabla}} \cdot \left( {\rho E{\boldsymbol{v}}} \right) = {\bf{\nabla}} \cdot \left( {\kappa {\bf{\nabla}} T} \right) + {\bf{\nabla}} \cdot \left( { - p{\boldsymbol{v}} + {\boldsymbol{\tau}} \cdot {\boldsymbol{v}}} \right) + {W_F} + {q_{\rm{H}}} (5) 式中:
E 为单位总能,J;\kappa 为热导率,W/(m·K);T 为温度,K;W{}_F 为彻体力功,J;q{}_{\rm{H}} 为热源项,{\rm{W}}/{\rm{m}} 。2. 流道转换器优化设计
设计流道转换器时主要考虑以下因素:一是实现流道转换功能;二是流道转换器加工的难易程度,曲面越简单,加工越容易;三是钻井液流经流道转换器时的压力损失低,可降低仪器串压耗,提高仪器现场使用的适应性;四是流道转换器内流道的流场要均匀,减小紊流,提高仪器抗冲刷性,延长仪器的使用寿命。
随钻测井仪流道转换器原始设计如图1(a)所示(图中,α为扩张角,(°);d为截面突变尺寸,mm),加工工艺简单,可以实现流道转换功能。流场性能分析结果表明,原始设计会导致较大的压力损失,同时在流道内形成较为严重的紊流。分析认为原始设计方案存在以下问题:1)截面尺寸突变,会使出口流场形成紊流;2)扩张角较大,使内流道截面积变化快(流速变化快),导致压力损失较大。因此,分别设计了3种优化方案(见图1(b)—(d)),优化方案1和原始设计相比扩张角为45°不变,减小截面突变尺寸;优化方案2和优化方案1相比,截面突变尺寸不变,扩张角由45°减小为30°;优化方案3的扩张角进一步减小至20°,截面尺寸由突变改为连续。扩张角越大,截面突变尺寸越大,加工工艺越好。原始设计及优化方案1和2为分体结构,加工工艺较简单;优化方案3为整体式结构,加工工艺复杂。4种设计方案的结构参数如表1所示。
表 1 流道转换器设计方案Table 1. Design schemes for the flow passage converter设计方案 α/(°) d/mm 结构类型 加工工艺 原始设计 45 16 分体式,流道突变 简单 优化方案1 45 6 分体式,流道突变 较简单 优化方案2 30 6 分体式,流道突变 较简单 优化方案3 20 0 整体式,流道连续 复杂 3. 流道转换器性能分析
3.1 数值模型的建立
采用NUMECA Automesh 4G生成非结构化全六面体网格。为保证对比分析的可行度,第一层网格的厚度及主流区的网格尺度相同。为了计算边界层的摩擦损失,要求
Y + < 10 (Y+ 为无量纲化的避免距离),第一层网格的厚度为0.01 mm。同时,为了保证计算的稳定性及准确性,将流道转换器进口和出口的长度延长为流道转换器外径的2倍,原始设计模型的网格总数约为100万个。流道转换器的流体计算域如图2所示,流体计算域网格划分如图3所示。3.2 数值方法及边界条件
采用NUMECA的HEXSTREAM求解器对流场进行求解,空间离散采用中心差分格式辅助人工黏性项,采用四步Rung-Kutta法进行迭代求解,用全多重网格法、局部时间步法和隐式残差光顺加速迭代收敛,湍流模型选用低雷诺数Spalart-Allmaras模型[15]。通过求解质量、动量和能量方程,对4种设计方案进行流体力学仿真分析。
为了比较流道转换器4种设计方案的性能,设置边界条件相同。进口边界给定总温总压条件,流动方向垂直于进口面;出口给定流量边界条件,固体壁面均设置为绝热黏性壁面。
3.3 数值模拟与对比分析
流道转换器中主要存在2种流动损失:一是钻井液和流道管壁之间的摩擦损失;二是非稳定流动(主要是漩涡)所引起的压力损失。采用总压损失系数来评估流道转换器流动损失为:
\sigma = \frac{{{{p}}_{{\rm{in}}} - p_{{\rm{out}}}}}{{{{p}}_{{\rm{in}}}}} (6) 式中:
\sigma 为总压损失系数;p_{\rm{in}} 为进口压力,Pa;p_{\rm{out}} 为出口压力,Pa。计算得到流道转换器4种设计方案的总压损失系数的对比情况(见表2),可以看出原始设计的总压损失最大,优化方案1—3的总压损失依次减小。
表 2 流道转换器4种设计方案流动压力损失计算结果Table 2. Calculated flow pressure loss in four design schemes of the flow passage converter设计方案 进口压力/kPa 出口压力/kPa 总压损失系数,% 原始设计 10 000 9 853.8 1.462 优化方案1 10 000 9 880.8 1.192 优化方案2 10 000 9 886.0 1.140 优化方案3 10 000 9 959.3 0.407 在流道转换器上沿流动方向(Z轴)按照等间距截取66个特征截面,提取各截面上的特征参数(如流通面积、轴向速度)进行对比分析,4种设计方案的内流道截面积沿流向变化情况如图4所示,其中横坐标流向为所截取的特征截面的序号。从图4可以看出,原始设计的截面突变尺寸较大,导致流通面积在前半部分有一个台阶状的陡然增大,在这个位置必然存在流动分离,造成了极大的流动损失。优化方案3的流通面积与其他3个方案相比变化最为平缓,说明设计更加合理,因此流动损失小。
内流道截面积的变化直接引起流体轴向速度的变化,流体轴向速度变化情况如图5所示。从图5可以看出,原始设计的流体轴向速度在流道前半部分出现阶跃式降低,这是由于流通面积变化所引起的。优化方案3的流体轴向速度在前半部分下降较快,后半部分下降较为平缓。与其他3个设计方案相比,优化方案3的流体轴向速度最为平缓,根据伯努利方程,压力升高更为平缓,逆压梯度更小,更容易抑制流动分离,流场也更为稳定。
4种设计方案纵截面上的湍流黏性云图如图6所示(图中,湍流黏性比是湍流黏度与动力黏度的比值,根据该参数可以得到涡流的扩散云图)。4种设计方案均为对称模型,优点在于其可改善出口流场的均匀度。但在流体力学中,对称模型并不能保证流场对称,形成流场不对称的原因是:从中心(环空)流道向环空(中心)流道的过渡过程中存在扩张角,扩张角越大,流通面积的变化越剧烈,从而造成压力梯度较大,引起了流动分离,最终导致流场时间上的不对称,其中原始设计尤为明显。此外,从图6还可以看出,原始设计流道流场内部存在大量漩涡,从而导致流动损失较大,说明设计不合理;优化方案3的流道流场均匀性最好,流动损失最小,说明截面设计最合理。
4种设计方案出口截面上流体轴向速度分布如图7所示。从图7可以看出,优化方案3的出口截面上轴向速度变化最小,流场也最均匀。
对比原始设计与优化方案1可知,扩张角相同情况下,流道截面突变尺寸越小,流通面积变化梯度越小,流场越均匀;对比优化方案1和2可知,截面突变尺寸相同的情况下,扩张角越小,流通面积变化梯度越小,压力损失越小;对比优化方案2和3可知,截面尺寸从突变改为连续后,流通面积变化梯度更小,压力损失更小,流场更均匀。综合考虑加工工艺复杂程度,原始设计加工简单,压力损失大,流场不均匀;优化方案3加工较复杂,但是压力损失较小,流场较均匀。
4. 试验验证
采用水力循环测试装置(见图8),以清水为流动介质,对4种设计方案进行水力循环试验,电动泵排量均为1.8 m3/min。为了比较4种设计方案的优劣,将4种流道转换器分别组装到随钻测井仪中,在进口与出口处分别安装压力传感器1与压力传感器2,测量流道转换器进出口的压力。
试验测得的4种流道转换器设计方案的压力损失情况如表3所示。对比表2与表3可知,4种设计方案的总压损失系数理论值与试验值对应的差值不大于0.076%,且变化趋势均与上述分析结果相同。
表 3 流道转换器4种设计方案的流动压力损失试验结果Table 3. Experimental flow pressure loss in four design schemes for the flow passage converter设计方案 进口压力/kPa 出口压力/kPa 总压损失系数,% 原始设计 520.0 512.0 1.538 优化方案1 585.0 577.7 1.248 优化方案2 514.0 508.0 1.167 优化方案3 477.0 475.0 0.419 5. 结论与建议
1)流体力学数值分析表明,流道转换器的扩张角越大,轴向速度变化梯度越大,流场均匀性越差,压力损失越大;内流道截面突变尺寸越大,轴向速度变化梯度越大,流场均匀性越差,压力损失也越大。
2)水力循环试验结果表明,4种设计方案的总压损失系数理论值与试验值的差值在合理范围内,且变化趋势均与数值计算分析相同。
3)设计流道转换器时,建议不仅考虑加工工艺的复杂性,还应该考虑扩张角和内流道截面突变对流场性能的影响。
-
表 1 流道转换器设计方案
Table 1 Design schemes for the flow passage converter
设计方案 α/(°) d/mm 结构类型 加工工艺 原始设计 45 16 分体式,流道突变 简单 优化方案1 45 6 分体式,流道突变 较简单 优化方案2 30 6 分体式,流道突变 较简单 优化方案3 20 0 整体式,流道连续 复杂 表 2 流道转换器4种设计方案流动压力损失计算结果
Table 2 Calculated flow pressure loss in four design schemes of the flow passage converter
设计方案 进口压力/kPa 出口压力/kPa 总压损失系数,% 原始设计 10 000 9 853.8 1.462 优化方案1 10 000 9 880.8 1.192 优化方案2 10 000 9 886.0 1.140 优化方案3 10 000 9 959.3 0.407 表 3 流道转换器4种设计方案的流动压力损失试验结果
Table 3 Experimental flow pressure loss in four design schemes for the flow passage converter
设计方案 进口压力/kPa 出口压力/kPa 总压损失系数,% 原始设计 520.0 512.0 1.538 优化方案1 585.0 577.7 1.248 优化方案2 514.0 508.0 1.167 优化方案3 477.0 475.0 0.419 -
[1] 侯亮. 2020国外测井技术进展与趋势[J]. 世界石油工业,2020,27(6):49–54. HOU Liang. Development and trend of foreign well logging technologies in 2020[J]. World Petroleum Industry, 2020, 27(6): 49–54.
[2] 布志虹,任干能,陈乐. 随钻测井技术[J]. 断块油气田,2001,8(4):22–24. doi: 10.3969/j.issn.1005-8907.2001.04.007 BU Zhihong, REN Ganneng, CHEN Le. Logging while drilling technology[J]. Fault-Block Oil & Gas Field, 2001, 8(4): 22–24. doi: 10.3969/j.issn.1005-8907.2001.04.007
[3] 涂春赵,张国强,刘如明,等. 随钻方位电阻率测井仪在渤海油田的应用与探索[J]. 石油管材与仪器,2020,6(6):70–73. TU Chunzhao, ZHANG Guoqiang, LIU Ruming, et al. Application of directional wave propagation resistivity tool in Bohai Oilfield[J]. Petroleum Tubular Goods & Instruments, 2020, 6(6): 70–73.
[4] 林楠,王敬萌,亢武臣,等. 最新随钻声波测井仪的技术性能与应用实例[J]. 石油钻探技术,2006,34(4):73–76. doi: 10.3969/j.issn.1001-0890.2006.04.022 LIN Nan, WANG Jingmeng, KANG Wuchen, et al. Technical performances and applications of the newly developed sonic LWD tools[J]. Petroleum Drilling Techniques, 2006, 34(4): 73–76. doi: 10.3969/j.issn.1001-0890.2006.04.022
[5] 朱祖扬,倪卫宁,张卫,等. 随钻一体化测井仪平台开发[J]. 石油钻探技术,2019,47(1):118–126. doi: 10.11911/syztjs.2019016 ZHU Zuyang, NI Weining, ZHANG Wei, et al. The development of an integrated logging instrument platform while drilling[J]. Petroleum Drilling Techniques, 2019, 47(1): 118–126. doi: 10.11911/syztjs.2019016
[6] 路保平,倪卫宁. 高精度随钻成像测井关键技术[J]. 石油钻探技术,2019,47(3):148–155. doi: 10.11911/syztjs.2019060 LU Baoping, NI Weining. The key technologies of high precision imaging logging while drilling[J]. Petroleum Drilling Techniques, 2019, 47(3): 148–155. doi: 10.11911/syztjs.2019060
[7] 李亨,刘迪仁,倪小威,等. 钻井液侵入情况下随钻电磁波电阻率测井的响应[J]. 断块油气田,2019,26(5):675–680. LI Heng, LIU Diren, NI Xiaowei, et al. Logging responses of electromagnetic wave resistivity while drilling with drilling fluid intrusion[J]. Fault-Block Oil & Gas Field, 2019, 26(5): 675–680.
[8] 李安宗,秦泓江,王珺,等. 随钻可控源中子测井仪器研究[J]. 石油钻采工艺,2011,33(5):105–109. doi: 10.3969/j.issn.1000-7393.2011.05.028 LI Anzong, QIN Hongjiang, WANG Jun, et al. Study on neutron logging while drilling tool controllable neutron source[J]. Oil Drilling & Production Technology, 2011, 33(5): 105–109. doi: 10.3969/j.issn.1000-7393.2011.05.028
[9] 王智明,王红亮,邓晓清,等. 随钻仪器机电接口标准化推进产品产业化[J]. 石油工业技术监督,2017,33(12):19–22. doi: 10.3969/j.issn.1004-1346.2017.12.005 WANG Zhiming, WANG Hongliang, DENG Xiaoqing, et al. Standardization of mechanical and electrical interfaces of LWD instruments to pomote product industrialization[J]. Technical Supervision in Petroleum Industry, 2017, 33(12): 19–22. doi: 10.3969/j.issn.1004-1346.2017.12.005
[10] 李杰,罗瑜林,刘西恩. 随钻用流道转换接头损伤规律研究及改进方法[J]. 石油矿场机械,2018,47(3):14–18. doi: 10.3969/j.issn.1001-3482.2018.03.003 LI Jie, LUO Yulin, LIU Xien. Research on the damage revolution law of flow channels crossover subs while drilling and the development method[J]. Oil Field Equipment, 2018, 47(3): 14–18. doi: 10.3969/j.issn.1001-3482.2018.03.003
[11] 杨顺辉,陶兴华,殷琨,等. 计算流体动力学在冲击器设计和模拟中的应用[J]. 石油钻探技术,2008,36(5):40–42. doi: 10.3969/j.issn.1001-0890.2008.05.010 YANG Shunhui, TAO Xinghua, YIN Kun, et al. Application of CFD on the design and simulation of hydro-efflux hammer[J]. Petroleum Drilling Techniques, 2008, 36(5): 40–42. doi: 10.3969/j.issn.1001-0890.2008.05.010
[12] 王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004: 4–17. WANG Fujun. Principle and application of CFD software for computational fluid dynamics analysis[M]. Beijing: Tsinghua Univer-sity Press, 2004: 4–17.
[13] 药晓江,董景新,尚捷,等. 随钻测井用涡轮发电机叶轮组水力性能分析[J]. 石油机械,2015,43(6):6–10, 75. YAO Xiaojiang, DONG Jingxin, SHANG Jie, et al. Hydraulic performance analysis of turbine impeller assembly for LWD[J]. China Petroleum Machinery, 2015, 43(6): 6–10, 75.
[14] 孔珑. 可压缩流体动力学[M]. 北京: 水利电力出版社, 1991: 3–18. KONG Long. Compressible fluid dynamics[M]. Beijing: Water Conservancy and Electric Power Press, 1991: 3–18.
[15] 张永学,李振林. 流体机械内部流动数值模拟方法综述[J]. 流体机械,2006,34(7):34–38. doi: 10.3969/j.issn.1005-0329.2006.07.009 ZHANG Yongxue, LI Zhenlin. Summary of numerical simulation methods for flow in fluid machinery[J]. Fluid Machinery, 2006, 34(7): 34–38. doi: 10.3969/j.issn.1005-0329.2006.07.009
-
期刊类型引用(6)
1. 许期聪,陈东,冯思恒. 大排量直井段随钻测斜工具的研制与应用. 石油钻探技术. 2024(02): 174-180 .  本站查看
本站查看
2. 单玉奇,殷晓丹. 石油探井用流道转换器加工方法研究. 现代制造技术与装备. 2024(05): 118-120 .  百度学术
百度学术
3. 杨恒灿,张玉霖,林颢屿,菅志军,鲍东升,黄玥. 旋转导向钻井系统三肋流道转换器设计研究. 石油矿场机械. 2024(06): 56-61 .  百度学术
百度学术
4. 卢华涛,药晓江,王清华,丁元皓,菅光霄. 随钻测斜仪扶正器优化设计与流体仿真. 中国石油和化工标准与质量. 2022(10): 73-75 .  百度学术
百度学术
5. 简旭,李皋,王军,韩旭,黄兵,王松涛. 气体钻井声波超前测距方法与数值模拟. 石油钻探技术. 2022(03): 132-138 .  本站查看
本站查看
6. 张正玉,袁军,李阳兵. 高强度高温高压直推存储式测井系统在超深井的应用. 石油钻探技术. 2022(05): 117-124 .  本站查看
本站查看
其他类型引用(0)



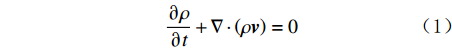
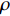
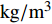
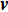
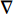
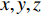
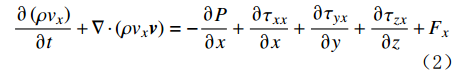
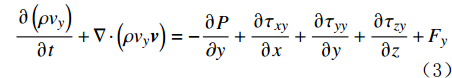
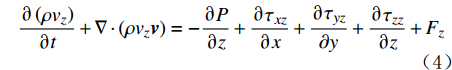
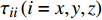
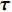
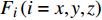
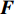
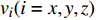
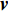
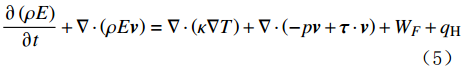
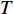
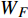
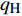
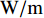

 下载:
下载: