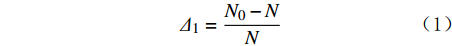Correcting Errors Due to Borehole and Formation Factors during Azimuthal Gamma Spectrum Logging While Drilling
-
摘要:
在不同井眼环境和地层条件下，随钻方位伽马能谱响应会有一定差异，从而影响后续的测井解释及地质导向结果，因此，有必要研究井眼和地层因素对随钻方位伽马能谱的影响规律，以消除其带来的不利影响。对比分析了现有随钻方位伽马能谱测井仪器结构，选择了其中一种结构作为研究对象，建立了相应的MCNP计算模型；采用蒙特卡罗方法模拟了随钻方位伽马能谱测井在不同井眼、地层条件下的响应，得到了钻井液密度、钻井液中KCl含量、地层骨架，以及倾斜放射性地层的倾角、方位角、厚度对随钻方位伽马能谱测井的影响规律，在此基础上，给出了非地层因素影响的校正方法。研究结果表明：计数率与钻井液中KCl含量和地层倾角及厚度正相关，与钻井液密度、地层骨架密度和地层倾斜界面方位角负相关；KCl能改变能谱形状，其他因素不改变能谱形状。研究表明，利用井眼影响因素校正后的计数率或能谱计算的泥质含量及K，U和Th的含量更接近真实值，可为测井解释及地质导向提供更可靠的指导。
Abstract:Under different borehole and formation conditions, there are some differences in the response of azimuthal gamma spectrum logging while drilling which can affect the subsequent logging interpretation and geosteering results. Therefore, it is necessary to study the influence of borehole and formation factors on the LWD azimuthal gamma spectrum, so as to eliminate the adverse effects and errors. First of all, the instrument structure of SAGR tool was compared and analyzed, and one of the structures was selected to be the study objective to establish the corresponding MCNP model. The response of LWD SAGR tool under different wellbore and formation conditions was simulated with the Monte Carlo method. The degree of influence for each of the following factors was obtained: mud density, KCl content, formation matrix and the dip angle, azimuth and thickness of inclined radioactive formation on the LWD SAGR Tool. Using the derived results it was possible to develop an appropriate, correction method for the influence of each of the non-stratigraphic factors. The results showed that the counting rate was positively correlated with KCl, dip angle and the formation thickness, and negatively correlated with mud density, the formation matrix density and azimuth. Only KCl rather than other factors can change the shape of energy spectrum. The study found that the counting rate after being corrected by the borehole influencing factors or the shale content, K, U, Th calculated by energy spectrum were closer to the true values, which could provide more accurate guidance for logging interpretation and geosteering.
-
随钻方位伽马能谱测井是在随钻方位伽马测井的基础上增加了测能谱，不仅能获得方位伽马成像图、计算地层相对倾角、识别地层界面及特殊地质构造（裂缝等），还能确定K，U和Th等元素的含量，从而确定泥质类型，估算总有机碳含量，为地质导向提供更准确、全面的信息。
关于随钻方位伽马测井仪器参数优化、探测特性分析、方位伽马成像的正反演等，国内学者已做了大量研究工作[1-6]，但并未涉及随钻方位伽马能谱测井，国外也是2000年以后才有相关研究文献。2002年M. Mickael等人[7]提出了采用3个NaI（Tl）晶体探测器的随钻方位伽马能谱测井仪SAGR，并于2007年介绍了该仪器的结构[8]，指出虽然理论上可以对K，U和Th的含量进行方位成像，但考虑能谱统计的精确性，最好是将不同探测器、不同扇区的能谱响应结合之后再计算K、U和Th的含量。随后，R. Nye，A.F. Marsala，C. Maranuk和M. Diab等人[9-12]研究了SAGR在页岩气、煤层气等非常规油气藏中的应用。2015年，Xu Libai等人[13]提出了与M. Mickael所提出仪器结构不同的随钻方位伽马能谱测井仪，采用2个居中的NaI晶体探测器。上述研究可为随钻方位伽马能谱测井仪器的结构设计提供参考，但并未分析井眼环境、地层特性对随钻方位伽马能谱测井的影响。
针对国内外在随钻方位伽马能谱测井的影响因素分析及校正研究方面的空白，笔者以文献[13]中的仪器结构为基础，建立了相应的MCNP计算模型，模拟研究了井眼环境（钻井液密度、钻井液中KCl含量）和地层条件（地层骨架及倾斜放射性地层的倾角、方位角和厚度）对随钻方位伽马能谱测井计数率及能谱的影响，并给出了井眼环境影响因素的校正方法。
1. MCNP计算模型的建立
1.1 探测器数量的选择
采用1个探测器时，随钻方位伽马能谱测井仪旋转1周，每个扇区采集1次；采用3个探测器时，测井仪旋转1周，每个扇区采集3次。探测器越多，计数率和能谱的统计精度越高。当探测器数量较多时（4个或更多），测井仪不用旋转，直接滑动便能获得方位伽马成像图，可减少工作量，缩短测井时间；并且，探头数量越多，方位数据采集密度越大，成像越准确。但是，探测器数量增多，不仅增加成本，还会影响测井仪结构的稳定性，所以选择探测器数量时应在保证计数统计精确性、滑动测量模式下数据采集密度、测井仪结构稳定的前提下尽量降低成本。综合考虑后，笔者以2个探测器互成180°的测井仪为研究对象。
1.2 MCNP计算模型
笔者研究的随钻方位伽马能谱测井仪对应MCNP计算模型的正视与俯视图如图1所示。图1中，1代表钻铤5和地层6之间的井眼间隙，2是钻井液通道，3和30是2个互成180°的NaI晶体探测器。以下模拟研究只对NaI晶体探测器3计数。
MCNP计算模型的参数设定为：模型半径60.44 cm，模型高200.00 cm，井眼间隙ΔR=5.00 cm；地层6为泥质砂岩，其质量组成为40%泥质，10% H2O和50% SiO2，密度为2.06 kg/L，40%泥质由16%高岭石、16%蒙脱石、1%U、1%Th和6%K组成。上述参数可根据研究的具体情况进行调整。
2. 井眼环境影响因素分析
采用图1所示的MCNP计算模型，分析钻井液密度、井眼间隙和钻井液中KCl含量对随钻方位伽马能谱计数率及能谱响应的影响情况。
2.1 钻井液（不含KCl）密度对响应特征的影响
钻井液由蒙脱石和水按不同质量分数混合得到。保持地层参数不变，模拟了不同钻井液密度和井眼间隙下的计数率和能谱响应特征。
2.1.1 计数率响应
不同钻井液密度、不同井眼间隙下的计数率响应情况如图2所示。
从图2可以看出：在相同井眼间隙下，钻井液密度越大，计数率越小；在钻井液密度相同的情况下，井眼间隙越大，计数率越小。分析认为，井眼间隙、钻井液密度变大，伽马射线在钻井液中的衰减增强，导致接收到的伽马射线减少，计数率变小。
2.1.2 能谱响应
对比相同钻井液密度（ρm=1.32 kg/L）、不同井眼间隙下的能谱，结果如图3所示。
![]()
图 2 不同钻井液密度、井眼间隙下的计数率Figure 2. Total count rate at different mud densities and wellbore gaps从图3可以看出，井眼间隙越大，特征能道计数率越小；而不同井眼间隙下的能谱基本重叠在一起，即能谱形状一致（各能道计数率的相对大小一致）。
对比不同钻井液密度、相同井眼间隙（ΔR=5 cm）下的能谱，结果如图4所示。
从图4可以看出，钻井液密度越大，特征能道计数率越小，而不同钻井液密度下的能谱形状一致。
综合上述分析可知，钻井液密度越大、井眼间隙越大，地层伽马射线的衰减越强，导致能谱的各能道计数率均变小，但并未改变能谱形状。
2.2 含KCl钻井液对响应特征的影响
用蒙脱石、KCl和水按不同质量分数配制不同密度的钻井液。为防止钻井液中KCl的响应被掩盖，将地层中K，U和Th的含量设为低值（0.001% U，0.001%Th和1%K），并适当减小地层半径。保持钻井液密度、地层不变，模拟了不同KCl含量、不同井眼间隙下的计数率和能谱响应。
2.2.1 计数率响应
钻井液密度、地层参数不变，不同KCl含量和井眼间隙下的计数率响应如图5所示。
![]()
图 5 不同KCl含量、井眼间隙下的计数率Figure 5. Counting rate at different KCl contents and wellbore gaps从图5（a）可以看出，在相同井眼间隙下，钻井液中KCl含量越高，绝对计数率越大，这是因为KCl本身具有放射性，其含量增加，相当于增加了放射源的放射强度。从图5（b）可以看出，KCl含量分别为0，5%和10%时，计数率与井眼间隙负相关，井眼间隙越大，计数率越小，此时钻井液对伽马射线主要起衰减作用；KCl含量为15%，20%和25%时，计数率与井眼间隙正相关，井眼间隙越大，计数率越大，此时KCl的影响以增大放射源强度为主。
2.2.2 能谱响应
相同井眼间隙（ΔR=5 cm）、不同KCl含量下的能谱响应如图6所示。
从图6（a）可以看出，钻井液中KCl含量增大，K特征能道处的计数率增大，其他能道的计数率变化较小；从图6（b）可以看出，KCl含量增大，能谱形状改变，K峰更尖，同时对其他特征能道也产生了较大影响。
3. 地层特性的影响分析
为了考察地层条件对随钻方位伽马能谱测井计数率及能谱的影响，分析了不同地层密度和倾斜泥岩层不同倾角、厚度和方位角下的响应特征。
3.1 地层骨架对响应特征的影响
采用图1所示的计算模型，将地层6设置为50%骨架+10%水+50%泥质（泥质中含有1% U、1%Th和6%K），井眼中介质为钻井液（40%蒙脱石+60%水）。保持钻井液和井眼间隙（ΔR=5 cm）不变，改变地层骨架成分（分别取石英、方解石和白云石，对应地层密度为2.06，2.08和2.12 kg/L），模拟分析计数率和能谱响应特征。
3.1.1 计数率响应
钻井液和井眼间隙固定不变，改变地层骨架成分，得到的计数率响应如图7所示。
从图7可以看出，地层密度越大，计数率越小。
3.1.2 能谱响应
钻井液和井眼间隙固定不变，不同骨架下的能谱响应结果如图8所示。
从图8（a）可以看出，地层密度增大，能谱某些特征道的计数率增大，但增幅很小；从图8（b）可以看出，骨架成分改变，能谱形状并没有改变。
综合上述分析可知，地层骨架成分（即改变地层密度）改变，会改变伽马射线的衰减能力，进而影响计数率，但并不改变能谱形状。
3.2 界面倾角对响应特征的影响
采用如图9所示计算模型分析NaI晶体探测器3穿过倾斜界面时的响应特征。原点在模型中心处，倾斜界面穿过原点，界面上部地层为纯砂岩（成分为10% H2O+90% SiO2，密度为2.27 kg/L），界面下部地层为泥质砂岩（其成分与图1中泥质砂岩相同，含1% U+1% Th+6% K，密度为2.06 kg/L），井眼间隙设为0 cm。图9中：a为倾斜界面倾角，（°）；hz为记录点到原点的距离，cm；p为仪器旋转角度（与倾斜界面方位角相反，度数相同），（°）。
模拟时，保持旋转角度p=0°，改变倾斜界面倾角a（–40°、–20°、0°、20°、40°、60°、80°，逆时针为正），分析不同倾角下NaI晶体探测器3从下向上穿过界面时的计数率和能谱响应特征。
3.2.1 计数率响应
保持p=0°，改变a，模拟不同倾角下探测器从下向上穿过界面时的计数率，结果如图10所示。
![]()
图 10 探测器穿过不同倾角界面时的计数率Figure 10. Counting rate when the detector passes through interfaces with different dip angles从图10可以看出，固定倾角a，NaI晶体探测器3从下向上移动时，计数率先保持不变，之后逐渐减小形成过渡区，最后保持不变，且倾角越大，过渡区越宽；过渡区内，固定hz，倾角越大，计数率越大。
保持 p =0°，取hz=0，对比不同倾角下的计数率，结果如图11所示。
![]()
图 11 原点处不同界面倾角下的计数率Figure 11. Counting rate at different interface dips at the origin从图11可以看出，倾角越大，计数率越大，这是因为倾角变大，导致探测器3右侧有更多的放射性地层进入其探测范围，而探测器3左侧离开探测范围的放射性地层比较少，整体表现为探测范围内放射性地层增加，故随着倾角变大，计数率增大，但倾角超过50°后增大趋势变缓。
3.2.2 能谱响应
取p=0°、hz=0，模拟了不同倾角下的能谱响应特征，结果如图12所示。
从图12（a）可以看出，随着倾角变大，能谱各能道的计数率普遍增大；从图12（b）可以看出，倾角变化，不会改变能谱形状，不影响K，U和Th含量的计算结果。
3.3 方位角对响应特征的影响
采用图9所示的计算模型，通过旋转随钻方位伽马能谱测井仪得到不同的倾斜界面方位角。界面倾角设为a=40°，改变旋转角度p（0°、45°、90°、135°和180°，顺时针为正），模拟不同旋转角度下、NaI晶体探测器3从下向上穿过界面时的计数率及能谱响应特征。
3.3.1 计数率响应
不同旋转角度下，探测器从下向上穿过界面时的计数率响应如图13所示。
从图13可以看出，旋转角一定，仪器从下向上移动时，计数率先保持不变，之后逐渐减小形成过渡区，最后保持不变，且不同旋转角度下过渡区的宽度相同。由此可知，影响过渡区宽度的并不是方位角，而是倾斜角；过渡区内，记录点到层界面的距离一定时，方位角越大，计数率越小。
取hz=0，对比仪器在不同旋转角度下的计数率，结果如图14所示。
![]()
图 14 原点处不同旋转角度下的计数率Figure 14. Counting rate at different rotating angles at the origin从图14可以看出，旋转角度（界面方位角）越大，计数率越小，这是因为旋转角度变大，NaI晶体探测器3探测范围内的放射性地层减少。
3.3.2 能谱响应
取a=40°、hz=0，对比不同旋转角度下的能谱响应特征，结果如图15所示。
从图15（a）可以看出，界面倾角变大，各能道的计数率普遍增大；从图15（b）可以看出，界面倾角变化，不改变能谱形状，不影响K，U和Th含量的计算结果。
3.4 倾斜地层厚度对响应特征的影响
采用如图16所示模型（H为倾斜地层厚度，cm），保持a=30°、p=0°不变，改变H（分别取20，40，60和80 cm），模拟分析了NaI晶体探测器3穿过不同厚度倾斜放射性地层时的计数率和能谱响应特征。
![]()
图 16 倾斜地层厚度的MCNP计算模型Figure 16. MCNP calculation model of inclined formation with a certain thickness3.4.1 计数率响应
探测器从下向上穿过不同厚度倾斜地层时的计数率响应如图17所示。
![]()
图 17 倾斜地层不同厚度下的计数率Figure 17. Counting rate at different inclined formation thicknesses从图17可以看出，地层厚度H固定，仪器从下向上移动时，厚层（H=60和80 cm）有平台，而薄层（H=20和40 cm）没有平台，地层厚度越大，半幅度法确定的地层厚度越可靠；固定hz，地层厚度H越大，计数率越大。
取hz=0，对比不同地层厚度下的计数率差异，结果如图18所示。
![]()
图 18 原点处倾斜地层不同厚度下的计数率Figure 18. Counting rate at different inclined formation thicknesses at the origin从图18可以看出，地层厚度越大，计数率越大，当地层厚度达到一定程度时，计数率不再增大，这是因为超过了NaI晶体探测器的纵向探测范围。
3.4.2 能谱响应
取a=30°、p=0°、hz=0并保持不变，对比不同地层厚度H（分别取20，40，60和80 cm）下的能谱响应特征，结果如图19所示。
![]()
图 19 倾斜地层不同厚度下的能谱响应Figure 19. Energy spectrum response at different inclined formation thicknesses从图19（a）可以看出，地层层厚越大，各能道的计数率越大；从图19（b）可以看出，不同地层层厚下，各能道的相对计数率基本相同，即地层厚度变化不会改变能谱形状。
4. 井眼环境影响的校正
井眼环境的影响属于不利影响，应该消除；而地层特性的影响反映了地层的某种特性，包含有用的地层信息，不能直接消除，故笔者只研究消除井眼环境影响的校正过程。钻井液中含有KCl时，相当于在井眼中放置了额外的放射源，因此，应先消除KCl对计数率的额外影响；然后，再对钻井液密度、井眼间隙进行联合校正。由图5可得KCl校正图版，如图20（a）所示；由图2可得钻井液密度校正图版，如图20（b）所示。
KCl校正图版中，校正率的计算公式为：
Δ1=N0−NN (1) 式中：Δ1为KCl校正图版的校正率；N为有井眼间隙和钻井液中含KCl时的计数率；N0为井眼间隙为0（或为标准井眼间隙）且钻井液中不含KCl时的计数率。
KCl校正方法为：1）确定井眼间隙ΔR和钻井液中KCl的质量分数；2）根据ΔR、KCl质量分数和KCl校正图版确定Δ1；3）根据N和Δ1，确定KCl校正后的计数率NCK，NCK=N(1+Δ1)。
钻井液密度校正图版中，校正率Δ2的计算方法同上。钻井液密度校正过程为：1）确定井眼间隙ΔR和钻井液密度ρm；2）根据ΔR和ρm在钻井液密度校正图版上选取或用插值法确定校正曲线，算出校正率Δ2；3）根据KCl校正后的计数率NCK和Δ2，确定KCl、钻井液密度及井眼间隙校正后的计数率NC，NC=NCK(1+Δ2)。
利用校正前后的伽马计数率计算泥质含量，并与真实的泥质含量进行对比，结果如图21所示（图21中，红色虚线代表计算值与真实值相等）。从图21可以看出，利用校正后计数率计算的泥质含量更接近真实值。
![]()
图 21 校正前后泥质含量计算值对比Figure 21. Comparison of the calculated values of muddy content before and after correction井眼钻井液中含有KCl时，利用校正前后的能谱计算K的含量，结果如图22表示。从图22可以看出，利用校正前能谱计算的K含量偏大，而利用校正后能谱计算的K含量与真实值很接近，证明该校正方法有效、可靠。
![]()
图 22 校正前后K含量计算值对比Figure 22. Comparison of calculated potassium content before and after calibration5. 结论与建议
1）在随钻方位伽马能谱测井中，钻井液密度、钻井液中KCl含量、地层骨架以及倾斜放射性地层的倾角、方位角、厚度对计数率和能谱中各能道的计数率都有影响。计数率与钻井液中KC1含量、地层倾角及厚度正相关，与钻井液密度、地层骨架密度和地层倾斜界面方位角负相关。
2）钻井液中含有KC1，相当于在井眼中放置了额外的放射性源，增加了放射源的放射强度，同时改变了放射性元素中K，U和Th的比例，因此可改变能谱形状；其他因素并未改变放射性元素比例，不改变能谱形状，不影响K，U和Th含量的计算结果。
3）如何充分利用斜地层的倾角、方位角、厚度对随钻方位伽马能谱响应的影响规律，以及如何从中提取有用的地层信息，是值得继续研究的问题。
-
![]()
图 2 不同钻井液密度、井眼间隙下的计数率
Figure 2. Total count rate at different mud densities and wellbore gaps
![]()
图 5 不同KCl含量、井眼间隙下的计数率
Figure 5. Counting rate at different KCl contents and wellbore gaps
![]()
图 10 探测器穿过不同倾角界面时的计数率
Figure 10. Counting rate when the detector passes through interfaces with different dip angles
![]()
图 11 原点处不同界面倾角下的计数率
Figure 11. Counting rate at different interface dips at the origin
![]()
图 14 原点处不同旋转角度下的计数率
Figure 14. Counting rate at different rotating angles at the origin
![]()
图 16 倾斜地层厚度的MCNP计算模型
Figure 16. MCNP calculation model of inclined formation with a certain thickness
![]()
图 17 倾斜地层不同厚度下的计数率
Figure 17. Counting rate at different inclined formation thicknesses
![]()
图 18 原点处倾斜地层不同厚度下的计数率
Figure 18. Counting rate at different inclined formation thicknesses at the origin
![]()
图 19 倾斜地层不同厚度下的能谱响应
Figure 19. Energy spectrum response at different inclined formation thicknesses
![]()
图 21 校正前后泥质含量计算值对比
Figure 21. Comparison of the calculated values of muddy content before and after correction
-
[1] 袁超．随钻方位伽马测井方法基础研究[D]．青岛: 中国石油大学（华东）, 2012． YUAN Chao. Fundamental study on LWD azimuthal gamma ray well logging[D]. Qingdao: China University of Petroleum (East China), 2012.
[2] 邵才瑞,曹先军,陈国兴,等. 随钻伽马测井快速正演算法及地质导向应用[J]. 地球物理学报, 2013, 56(11): 3932–3942. doi: 10.6038/cjg20131135 SHAO Cairui, CAO Xianjun, CHEN Guoxing, et al. A fast forward algorithm for LWD gamma-ray response and its geosteering application[J]. Chinese Journal of Geophysics, 2013, 56(11): 3932–3942. doi: 10.6038/cjg20131135
[3] 向长生,王智锋,亢武臣. 随钻自然伽马地层边界模型分析[J]. 石油钻采工艺, 2013, 35(1): 112–114. doi: 10.3969/j.issn.1000-7393.2013.01.032 XIANG Changsheng, WANG Zhifeng, KANG Wuchen. Modeling and analysis of formation boundaries based on LWD natural gamma[J]. Oil Drilling & Production Technology, 2013, 35(1): 112–114. doi: 10.3969/j.issn.1000-7393.2013.01.032
[4] 范宇翔,骆庆锋,李留,等. 伽马成像随钻测井仪钻铤布局设计可靠性分析[J]. 石化技术, 2015, 22(10): 213–214. doi: 10.3969/j.issn.1006-0235.2015.10.156 FAN Yuxiang, LUO Qingfeng, LI Liu, et al. Analysis on design reliability of drill collar of gamma imaging logging while drilling instrument[J]. Petrochemical Industry Technology, 2015, 22(10): 213–214. doi: 10.3969/j.issn.1006-0235.2015.10.156
[5] 曲汉武, 吴文圣, 梁云祥, 等．随钻伽马成像的方位分辨率计算方法研究[A]．北京: 2016中国地球科学联合学术年会, 2016-10. QU Hanwu, WU Wensheng, LIANG Yunxiang, et al. Research on azimuth resolution calculation method of gamma imaging while drilling[A]. Beijing: 2016 Annual Meeting of Chinese Geoscience Union, 2016-10.
[6] 路保平,倪卫宁. 高精度随钻成像测井关键技术[J]. 石油钻探技术, 2019, 47(3): 148–155. doi: 10.11911/syztjs.2019060 LU Baoping, NI Weining. The key technologies of high precision imaging logging while drilling[J]. Petroleum Drilling Techniques, 2019, 47(3): 148–155. doi: 10.11911/syztjs.2019060
[7] MICKAEL M, PHELPS D, JONES D. Design, calibration, characterization, and field experience of new high-temperature, azimuthal, and spectral gamma ray logging-while-drilling tools[R]. SPE 77481, 2002.
[8] MICKAEL M W, JONES D A, PHELPS D A, et al. Spectral gamma ray logging-while-drilling system: US7253401B2[P]. 2007-08-07[2019-01-07].
[9] NYE R, TOMMASO D D. Well optimization using a LWD spectral azimuthal gamma ray tool in unconventional reservoirs[R]. OMC-2013-137, 2013.
[10] MARSALA A F, KASPRZYKOWSKI P, KIMOUR F. Spectral gamma ray complements innovative real time advanced mud logging characterization while drilling[R]. SPE 168099, 2013.
[11] MARANUK C, MICKAEL M, ZIMMERMANN P. Applications of a unique spectral azimuthal gamma ray tool to unconventional reservoirs[R]. SPWLA-2013-II, 2013.
[12] DIAB M, COMBS J. Unconventional horizontal well placement challenges: LWD geosteering applications utilizing a unique spectral azimuthal gamma ray in real time[R]. SPE 169499, 2014.
[13] XU Libai, HUISZOON C, WANG Jiaxin, et al. Spectral gamma-ray measurement while drilling[R]. SPWLA-2016-V57N4A4, 2016.
-
期刊类型引用(4)
1. 韩玉娇. 随钻方位成像测井数据压缩与还原方法. 西安石油大学学报(自然科学版). 2024(06): 95-99+139 . 
百度学术
2. 王港，秦臻，苏可嘉，胡雪琴，魏康健，邓呈祥. 非平行界面地层水平井自然伽马测井蒙特卡罗模拟. 江西科学. 2023(03): 478-481+527 . 百度学术
3. 肖功勋. 分析螺旋井眼的预防及测井数据校正. 中国石油和化工标准与质量. 2021(07): 7-8 . 百度学术
4. 彭礼韬，张立国，郝琦，玉宇. MCNP与GEANT4应用于随钻方位伽马测井仪探测性能对比. 测井技术. 2021(03): 267-272 . 百度学术
其他类型引用(5)
下载:
计量
- 文章访问数: 1362
- HTML全文浏览量: 454
- PDF下载量: 93
- 被引次数: 9
