Numerical Study on Drilling Fluid Leakage under Fluid-Solid Coupling in Deep Fractured Gas Reservoir
-
摘要:
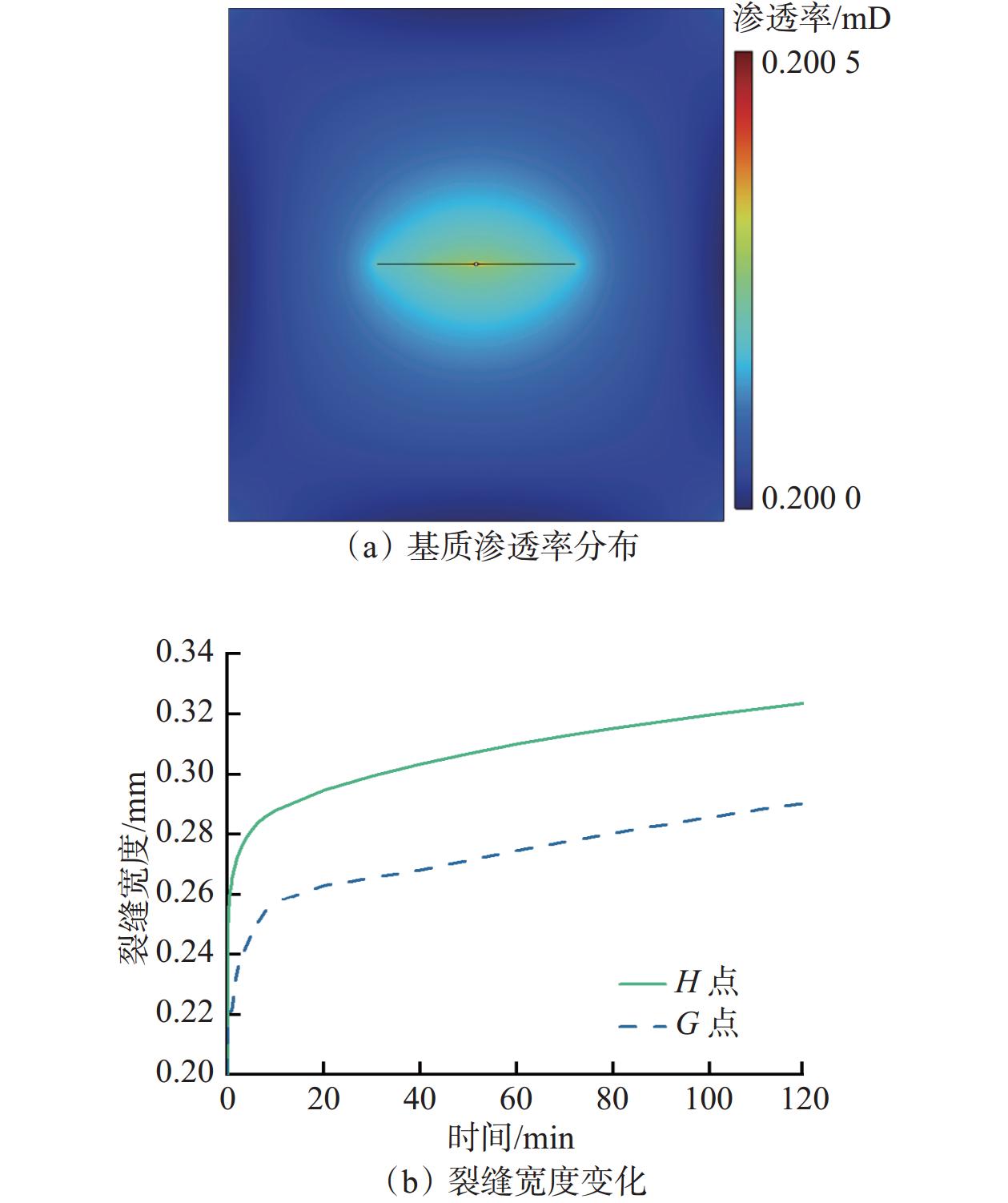
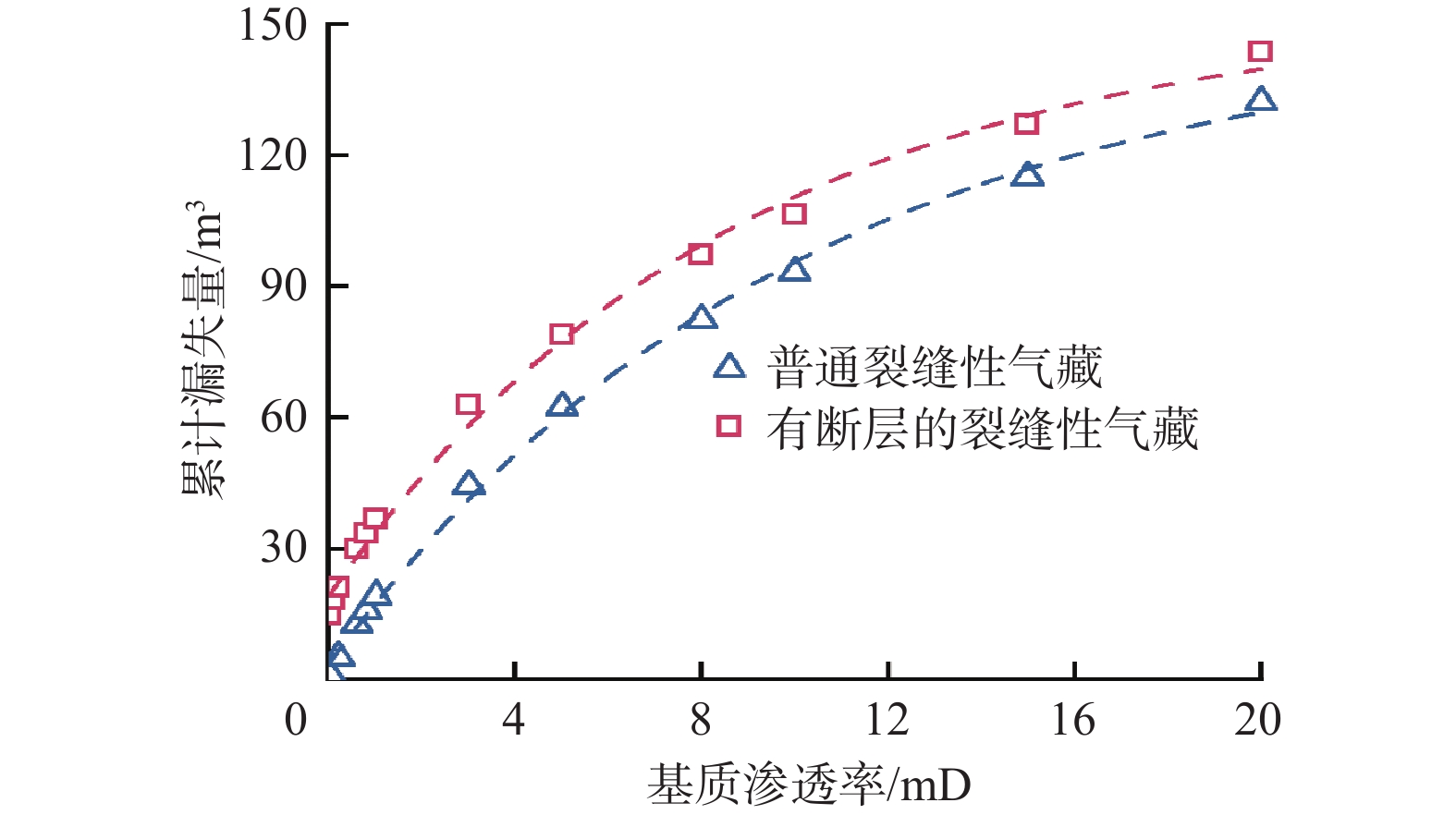
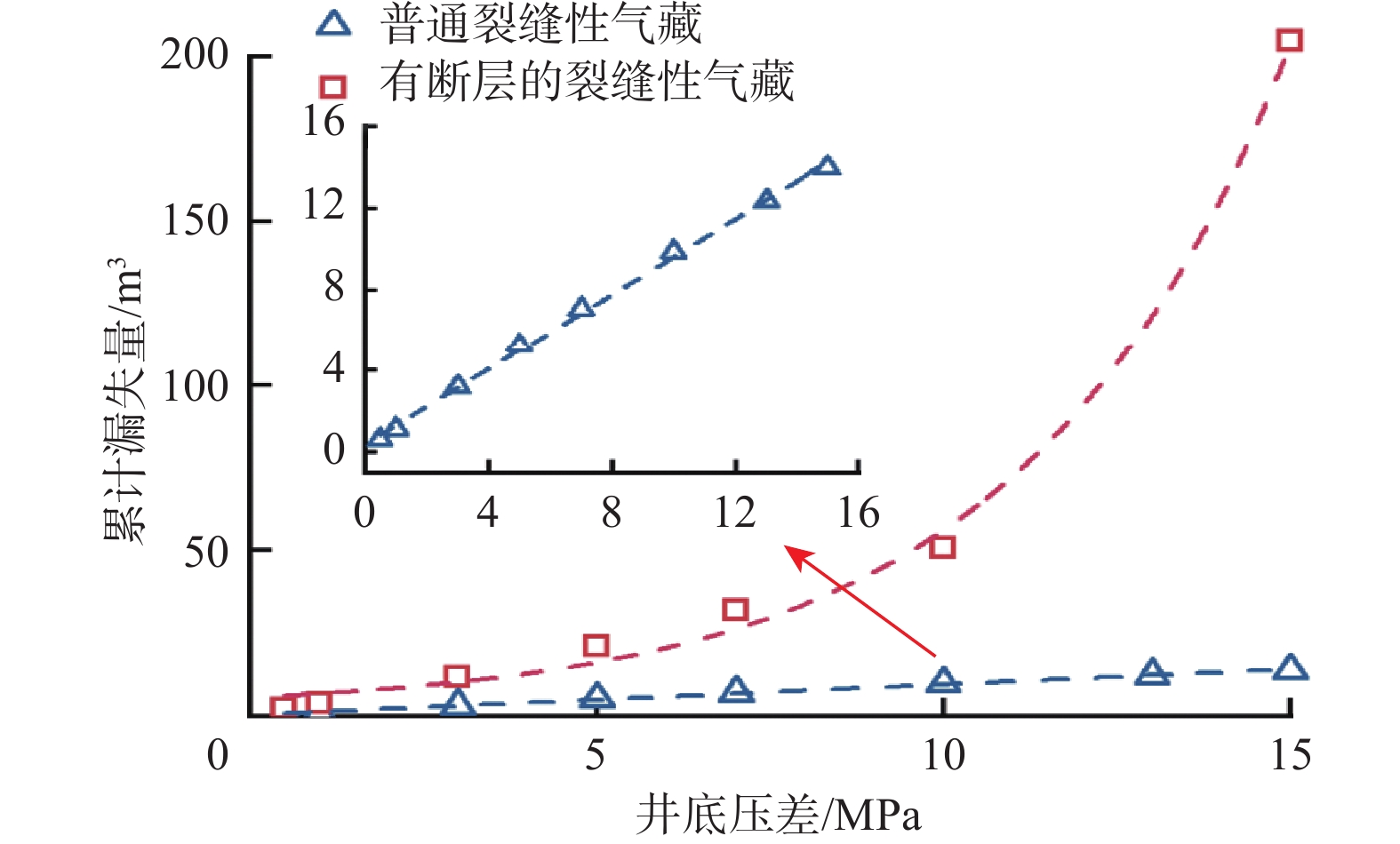
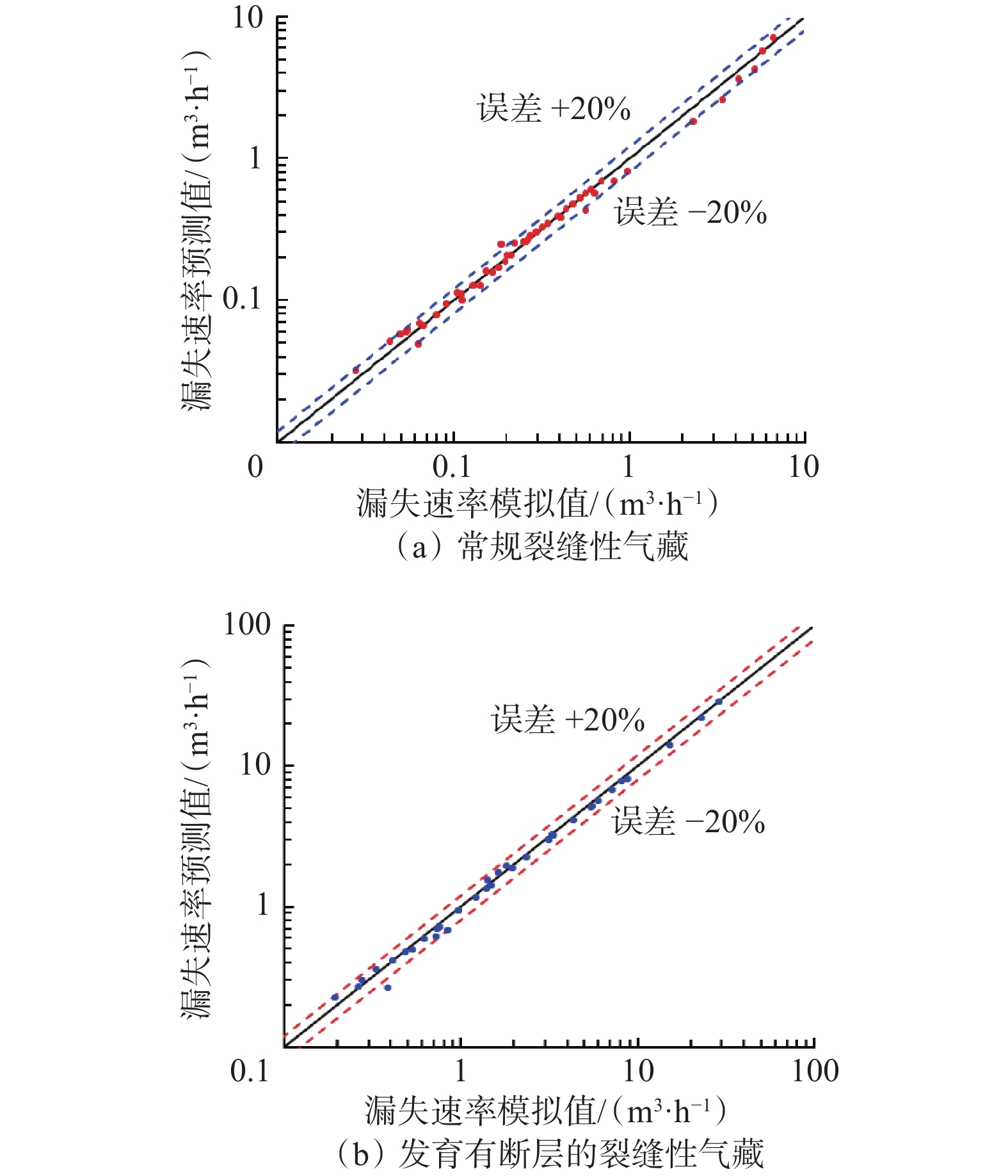
裂缝性地层钻井过程中井漏问题严峻，易导致产能降低和钻井安全事故。为此，综合考虑钻井液与天然气的物性差异、基质与裂缝间的耦合流动及裂缝开度的动态演化规律，建立了基于气液两相流动的裂缝性气藏漏失预测模型，并与实验数据进行对比，验证了模型的准确性；基于该模型，系统分析了气藏地质构造、基质参数、裂缝参数和井底压差等因素对漏失的影响规律，修正了传统统计学漏失模型，提出了适用于裂缝性气藏的漏失速率表征方法。研究结果表明，裂缝性气藏的漏失速率随着裂缝宽度增大呈对数函数增长，增长趋势先急后缓，随着井底压差和裂缝长度增大呈线性增长；发育有断层的裂缝性气藏的漏失速率随着裂缝宽度和井底压差增大呈指数增长，随着井眼与断层的距离增大呈对数式下降。研究结果为完善裂缝性气藏井漏规律和优选防漏堵漏技术提供了理论依据。
Abstract:During the drilling process in fractured formations, the issue of well leakage is severe, which can easily lead to reduced productivity and drilling safety accidents. To address this problem, this study comprehensively the differences of physical properties between mud and gas, coupled flow between matrix and fractures and the hydro-mechanical coupling. A mud loss model for fractured gas reservoirs with a gas–liquid two-phase flow was established, and its accuracy was verified by comparing it with physical experiments. Based on this model, the influence of geological structure, matrix parameters, fracture parameters, and bottom-hole pressure difference on lost circulation was analyzed. Furthermore, the traditional statistical mud-loss model was refined, and a method of leakage rate characterization suitable for fractured gas reservoirs was established. The results indicate that the loss rate increases linearly with the increase in bottom-hole pressure difference and fracture length in conventional fractured gas reservoirs, and increases in a logarithmic function with an increase in fracture width, the growth trend is first rapid and then slow. But for fractured gas reservoirs with developed faults, the loss rate increases exponentially with the increase in fracture width and bottom-hole pressure difference, and decreases logarithmically with an increase in the distance between the wellbore and fault. The conclusions drawn can provide theoretical references for further understanding the lost circulation and plugging technologies in deep fractured gas reservoirs.
-
注水是提高原油采收率的有效方法。为提高注水效率，国内各油田对注水方式开展了优化研究[1–4]，例如，分层注水可以解决不同层间矛盾，将注入水合理分配至各层段，保持地层压力，但该注水方式只是针对存在层间矛盾的油藏[5–7]。刘欢[8]通过优化地面注水系统的研究，提出油田企业应重视地面注水系统的优化。油田地面注水系统由注水站、配水间、注水井以及连接各注水单元的注水干线和支线组成。在满足配注要求的前提下，由注水站增压，注入水经配水间分配至各注水井。但在实际注水过程中，由于各注水井的注入压力差异较大，为满足其配注要求需按照系统内最高注入压力确定注水泵压。巨大的阀组损失对注水系统节能平稳运行十分不利。为此，在20世纪90年代国内学者就提出了分压注水的方法[9]，将注入压力相近的注水井组合在一起，配备相应的注水泵和注水系统，使各个系统的平均注入压力与泵压更加接近，从而达到降低能耗、提高效率的目的[10]。目前国内主要的分压注水方式主要包括单井增压、区域分压和整体分压3种形式[11]。国内许多学者对分压注水技术的探究大都是划分不同压力范围注水井，分别配备增压设备，这样虽可以大幅降低能耗损失，却带来了大量的基建投入，且改造过程复杂，不易实施[12–14]。王辉、冯杰等人[15–16]提出了一种单一系统内分时分压周期注水的方法，根据注水井实际压力分布分时段注水，以减少基建投入，但未能提出相应的优化模型及求解方法。
为此，笔者基于分压注水原理，考虑分时电价，建立了以泵站总能耗费用最低为目标的分压周期注水数学模型，借助数学规划和优化高级建模系统，调用分枝减小最优化导航求解器，结合分时电价确定了最佳注水方案。
1. 分时电价下分压周期注水模型
1.1 目标函数
注水站能耗是注水系统的动力来源，而注水站能耗又以注水站内泵机组能耗为主。因此，以各时段泵机组对注入水所做功、泵机组各类效率和电价等推导注水站总能耗成本函数：
F=min (1) 式中：F为注水站能耗总成本，元；m为总时段数；n为并联泵数量；i为周期内各时段编号；j为站内注水泵编号；pi为第i时段的电价，元/kWh；γij为第i时段第j台注水泵的启停状态（停用时取0，启用时取1）；Qi为第i时段注水站出口流量，m³/h；Hi为第i时段注水站出口扬程，m；ρ为注入水密度，kg/m³；g为重力加速度，m/s2；∆Ti为第i时段内注水时长，h；ηbij为第i时段第j台注水泵的效率；ηcij为第i时段第j台注水泵的传动效率，通常取0.96～0.98；ηdij为第i时段第j台注水泵配备电机的效率，通常取0.92～0.95；ηpij为第i时段第j台注水泵配备电机的变频效率，通常取0.98。
1.2 约束条件
模型约束条件分为站内与站外约束2部分，站内约束包括注水泵扬程和注水泵效率约束，站外约束包括注水井最大扬程和管道沿程摩阻约束。
1.2.1 站内约束
变频调速下注水泵扬程与流量应满足的约束[17]：
{H_{ij}} = k_{ij}^2{H_0} - {S_j}{Q_{ij}^2} (2) 式中：Hij为第i时段第j台注水泵的扬程，m；kij为第i时段第j台注水泵的调速比；H0为流量为0时的虚总扬程，m；Sj为第j台注水泵的内虚阻耗系数；Qij为第i时段第j台注水泵流量，m³/h。
变频调速下注水泵运行效率与流量应满足的约束：
\eta_{bij}=a_j+\frac{b_j}{k_{ij}}Q_{ij}+\frac{c_j}{k_{ij}^2}Q_{ij}^2 (3) 式中： aj，bj和cj分别为第j台泵的特性参数。
1.2.2 站外约束
对于各单井，需满足最高扬程注水井的要求[18]：
H_i\geqslant H_w+H_{w\mathrm{f}}+\Delta h_w (4) 式中：Hw为第w个注水井注入扬程要求，m；Hwf为第w个注水井总沿程摩阻损失，m；∆hw为第w个注水井与注水站的地势高度差，m；
各管段沿程摩阻损失采用海澄威廉公式计算[19]：
\Delta {H_k} = 10.67\frac{{Q_k^{1.852}{L_k}}}{{{C^{1.852}}d_k^{4.87}}} (5) 式中：∆Hk为管段k沿程摩阻损失绝对值，m；Qk为管段k流量绝对值，m³/s；dk和Lk为管段k的管径和管长，m；C为不同管材的计算系数，塑料管取150、新铸铁管取130、混凝土管取120。
1.3 求解策略
选择GAMS建模求解，由于分压周期注水优化模型含有非线性约束条件，属于非线性规划（NLP）模型。在GAMS中，BARON求解器是整体求解NLP模型和混合整数非线性规划（MINLP）模型的求解程序，传统的NLP和MINLP算法在确定凸假设下才能保证收敛，而BARON执行确定性的分枝定界（Branch-And-Bound）类型的整体最优算法，在一般假设下可保证提供整体最优。
2. 算例分析与注水优化
以辽河油田“一联”注水系统为例，开展分时分压周期注水优化研究。“一联”注水系统包括一座联合注水站、8座配水间、54口注水井，注入压力5～20 MPa，日注水量近10 000 m³。根据现场并联泵机组的高效区间范围，其流量应处于350～700 m³/h，注入压力应处于9～17 MPa。为使所有注入压力范围注水井在实际注水时处于高效区，将9 MPa设为低中压临界点、13 MPa设为中高压临界点，低压注水井共23口，中压注水井共12口，高压注水井共19口，管网结构及各单元位置如图1所示。
![]()
图 1 “一联”分压注水管网布局Figure 1. “Yilian” partial-pressure water injection pipeline network layout2.1 注水参数计算
考虑到现场实际注水量的波动情况，以24 h为最小周期。分时段注水会导致系统流量变化，影响管道流速，因此按国标规定的流速（单井支管流速不宜大于1.2 m/s、注水干管流速不宜大于1.6 m/s）进行计算[20]。结果表明各井组分别进行8 h注水，可满足流速要求。
在模型中，各注水井流量、注入压力及管网整体拓扑参数为已知参数，低中高压注水井组各泵流量、转速比为决策变量，通过GAMS建模并求解，得到低中高压注水井组最优的注水参数，见表1。
表 1 低中高压注水井组的最优注水参数Table 1. Optimization parameters of low-, medium-, and high-pressure water injection well groups注水井组 注水量/（m³·h−1） 1#泵转速比 1#泵效，% 2#泵转速比 2#泵效，% 注水功率/kW 低压注水井组 590 0.762 64.7 0.789 64.3 2435.49 中压注水井组 380 0.868 66.9 0.868 67.3 2159.08 高压注水井组 540 0.982 73.0 0.990 73.6 3498.66 优化后低压注水井组节流损失平均降低约7 MPa，中压注水井组节流损失平均降低约3 MPa，其降低百分比如图2所示。在对系统进行分压注水后，低压注水井阀前后压差相较未分压前平均降低了79.12%，中压注水井阀前后压差相较未分压前平均降低了67.67%，节能效果十分显著。
![]()
图 2 低压、中压注水井组阀前后压差降低百分比Figure 2. Percentage reduction of pressure difference before and after valve regulation in low-pressure and medium-pressure water injection well groups2.2 注水方案优化
根据分时电价负荷曲线形状，将一天划分为峰、平、谷3个时段，不同时段电价不同，通过价格杠杆，改变电力负荷构成，实现“削峰填谷”[21]。确定高中低压注水井组注水时长与流量后，需优化分配注水时段，充分利用分时电价带来的经济效益。选取辽宁2021年工业用电价格标准，见表2。
表 2 辽宁2021年工业用电标准Table 2. Liaoning industrial electricity consumption standard in 2021时段区间 总时段长度/h 价格标准/(元·kW−1·h−1) 峰时 10:00～12:00
20:00～24:006 1.025 谷时 24:00～08:00 8 0.425 平时 08:00～10:00
12:00～20:0010 0.725 各注入压力范围注水井组难以实现平均连续分配注水，同一注入压力范围注水井组会出现在不同电价时段。因此，为实现最大经济效益，需要优化注水时段。为此，提出一个周期内各注入压力范围注水井组交叉注水和顺次注水2种不同注水方式。
2.2.1 交叉注水
交叉注水指对不同注入压力范围注水井组交错注水，将各注入压力范围注水井组的注水站功率按高低排序，再依次匹配各时段电价，以充分利用分时电价的经济效益。根据能耗成本最优分配各时段流量、各时段注水量及注水站功率如图3所示。
![]()
图 3 交叉注水下各时段电价与注水量、电价与功率Figure 3. Electricity price, water injection quantity, and power in each period under cross water injection交叉注水可使高功率时段匹配低电价时段，充分利用分时电价价格区间，获得更高经济效益。但在注水周期内需多次调节泵站设备与注水井阀门，加大了现场人员工作量，对设备也有所损害。
2.2.2 顺次注水
顺次注水是指对不同注入压力范围的注水井组顺次注水，此方式可有效降低现场人员工作量，同时对相关设备损害较少，但存在高低功率与分时电价不匹配的问题，造成经济损失。
根据3类压力范围注水井的注水顺序，共设置“低中高、低高中、中低高、中高低、高低中、高中低”等6类方案，并借助软件分析各方案，以总能耗成本最低为目标确定最优注水方案，6类方案的总能耗成本计算结果如图4所示。
![]()
图 4 顺次注水起点时刻与总能耗费用Figure 4. Starting point and total energy cost under sequential water injection由图4可知，“低中高”、“中高低”、“高低中”方案最低总能耗成本相同，为42 596.16元，“低高中”、“中低高”、“高中低”方案最低总能耗成本相同，为42 762.00元。考虑经济效益，以“低中高”方案为例进行进一步分析，该方案中各时段注水量及注水站功率如图5所示，采用顺次注水时，仍存在高能耗匹配高电价时段、低能耗匹配低电价时段的现象，存在经济损失。
![]()
图 5 顺次注水各时段电价与注水量、电价与功率Figure 5. Electricity price and water quantity, electricity price and power in each period under successive water injection2.2.3 方案比较
针对不同注水方案，对比分析各时段能耗费用，如图6所示。24个时段内存在多个能耗费用相同时段，不同能耗费用由顺次注水与交叉注水在某个时段对应的注水量及注水站功率不同导致的。经计算，交叉注水方案总能耗成本达到了42 430.31元，顺次注水方案总能耗成本达到了42 596.16元。两者差距不大，但后者可降低实际运行工作量且设备损坏较少，更具推广价值。
![]()
图 6 不同方案下各时段能耗费用对比Figure 6. Comparison of energy consumption costs of different schemes in different periods3. 现场实际对比
以辽河油田某采油厂为例，该采油厂采用各时段均匀注水，因需满足现场各注水井实际需求，节流损失率高达近20%，“大马拉小车”问题十分突出。采用多时段分压注水方法，将注水压力相近的注水井组合在一起，配备合适的注水泵和相应的注水系统，使每个系统的平均注入压力与泵压更加接近；针对不同注入压力范围的注水井组，采取不同时段的注水方式，在各注入压力范围注水井进行单独注水时关停其余注水井，以减少高低压注水井对系统的干扰，从而降低系统节流损失以提高能效。
实际注水方案与优化后注水方案对比见表3。分时分压周期注水平均注水时段功率为2 697.74 kW，相较于实际注水减少600 kW。交叉注水一周期总成本为42 430.31元，顺次注水一周期总成本为42 596.16元，相较于未采用分时段分压注水时，一周期内成本均可降低约13000元，效益十分可观。采用分时段分压注水方法，可在不改变原有注水管网的基础上，显著降低能耗和成本。
表 3 实际注水方案与优化注水方案对比Table 3. Comparison of actual and optimized injection schemes注水方案 注水总
时长/h开泵数量 平均注水时段
功率/kW周期内总能耗
成本/元交叉注水 24 2 2697.74 42430.31 顺次注水 24 2 2697.74 42596.16 实际注水 24 2 3313.24 55662.43 4. 结 论
1）常规油田注水系统因泵压与井口压力不匹配，导致大量能量因节流损失，不利于系统节能运行。
2）采用分时分压多周期注水方式，相较于常规现场注水方案，可显著降低节流能量损失和成本。
3）交叉注水节能效果更佳，但增加了现场人员的工作量，对设备也有一定影响；顺次注水最大限度降低了系统运行时的操作次数，但总成本略高。考虑到整体操作与经济性，顺次注水具有更强的操作性与推广应用价值。
-
![]()
图 4 不同漏失模型的数值模拟结果对比
Figure 4. Comparison of numerical results between our model and XFEM
![]()
图 6 不同渗流模型的漏失速率对比
Figure 6. Comparison of loss curves between single-phase model and gas-liquid two-phase flow model
![]()
图 7 漏失过程基质渗透率和裂缝宽度的演化
Figure 7. Evolution of matrix permeability and fracture width during leakage process
![]()
图 9 不同裂缝性气藏的累计漏失量变化规律
Figure 9. Variation of loss rate and cumulative loss with fracture length and the distance between fault and wellbore
![]()
图 10 累计漏失量随基质渗透率的变化曲线
Figure 10. Variation of cumulative loss with matrix permeability
![]()
图 11 累计漏失量随钻井液黏度的变化曲线
Figure 11. Variation of cumulative loss with the viscosities of drilling fluid
![]()
图 12 累计漏失量随井底压力的变化曲线
Figure 12. Variation of cumulative loss with bottom hole pressure
-
[1] 刘岩生,张佳伟,黄洪春. 中国深层—超深层钻完井关键技术及发展方向[J]. 石油学报,2024,45(1):312–324. doi: 10.7623/syxb202401018 LIU Yansheng, ZHANG Jiawei, HUANG Hongchun. Key technologies and development direction for deep and ultra-deep drilling and completion in China[J]. Acta Petrolei Sinica, 2024, 45(1): 312–324. doi: 10.7623/syxb202401018
[2] 杨鹏程,薛浩楠,李升,等. 超深层高压油气藏天然气偏差系数计算新模型[J]. 石油钻探技术,2023,51(6):106–114. doi: 10.11911/syztjs.2023112 YANG Pengcheng, XUE Haonan, LI Sheng, et al. A new model for calculating deviation factor of natural gas in ultra-deep oil and gas reservoirs under high pressure[J]. Petroleum Drilling Techniques, 2023, 51(6): 106–114. doi: 10.11911/syztjs.2023112
[3] 房超,张辉,陈朝伟,等. 地质工程一体化漏失机理与预防措施:以塔里木库车山前古近系复合盐层为例[J]. 石油钻采工艺,2022,44(6):684–692. FANG Chao, ZHANG Hui, CHEN Zhaowei, et al. Geology-engineering integrated investigation of leakoff mechanisms and prevention measures: a case study of the Palaeogene composite salt layer in the Kuqa piedmont zone, Tarim Basin[J]. Oil Drilling & Production Technology, 2022, 44(6): 684–692.
[4] 曲鸿雁,胡佳伟,周福建,等. 深层裂缝性致密砂岩气藏基质–裂缝气体流动机理[J]. 石油钻探技术,2024,52(2):153–164. doi: 10.11911/syztjs.2024045 QU Hongyan, HU Jiawei, ZHOU Fujian, et al. Mechanism of gas flow in matrix-fracture in deep fractured tight sandstone gas reservoirs[J]. Petroleum Drilling Techniques, 2024, 52(2): 153–164. doi: 10.11911/syztjs.2024045
[5] XIA Yang, JIN Yan, CHEN Mian, et al. Hydrodynamic modeling of mud loss controlled by the coupling of discrete fracture and matrix[J]. Journal of Petroleum Science and Engineering, 2015, 129: 254–267. doi: 10.1016/j.petrol.2014.07.026
[6] LI Lei, YANG Jin, SONG Yu, et al. Numerical study of the mud loss in naturally fractured oil layers with two-phase flow model[J]. Journal of Petroleum Science and Engineering, 2022, 210: 110040. doi: 10.1016/j.petrol.2021.110040
[7] 张矿生,宫臣兴,陆红军,等. 基于集成学习的井漏智能预警模型及智能推理方法[J]. 石油钻采工艺,2023,45(1):47–54. ZHANG Kuangsheng, GONG Chenxing, LU Hongjun, et al. Intelligent early warning model and intelligent reasoning method based on integrated learning for loss circulation[J]. Oil Drilling & Production Technology, 2023, 45(1): 47–54.
[8] 朱明明,孙欢,孙艳,等. 陇东致密油区域恶性出水漏层堵漏技术[J]. 石油钻探技术,2023,51(6):50–56. doi: 10.11911/syztjs.2023003 ZHU Mingming, SUN Huan, SUN Yan, et al. Loss circulation control technology for malignant water leakage layer in Longdong tight oil region[J]. Petroleum Drilling Techniques, 2023, 51(6): 50–56. doi: 10.11911/syztjs.2023003
[9] 康毅力,田国丰,游利军,等. 缝面摩滑:深部裂缝性地层钻井液漏失加剧的新机制[J]. 石油钻探技术,2022,50(1):45–53. doi: 10.11911/syztjs.2021033 KANG Yili, TIAN Guofeng, YOU Lijun, et al. Friction & sliding on fracture surfaces: a new mechanism for increasing drilling fluid leakage in deep fractured reservoirs[J]. Petroleum Drilling Techniques, 2022, 50(1): 45–53. doi: 10.11911/syztjs.2021033
[10] LIETARD O, UNWIN T, GUILLOT D, et al. Fracture width LWD and drilling Mud/LCM selection guidelines in naturally fractured reservoirs[R]. SPE 36832, 1996.
[11] SANFILLIPPO F, BRIGNOLI M, SANTARELLI F J, et al. Characterization of conductive fractures while drilling[R]. SPE 38177, 1997.
[12] LAVROV A, TRONVOLL J. Mechanics of borehole ballooning in naturally-fractured formations[R]. SPE 93747, 2005.
[13] 李大奇,曾义金,刘四海,等. 基于分形理论的粗糙裂缝钻井液漏失模型研究[J]. 石油钻探技术,2017,45(4):46–52. LI Daqi, ZENG Yijin, LIU Sihai, et al. Drilling fluid loss model in rough fractures based on fractal theory[J]. Petroleum Drilling Techniques, 2017, 45(4): 46–52.
[14] MAJIDI R, MISKA S Z, AHMED R, et al. Radial flow of yield-power-law fluids: Numerical analysis, experimental study and the application for drilling fluid losses in fractured formations[J]. Journal of Petroleum Science and Engineering, 2010, 70(3/4): 334–343.
[15] 李大奇,刘四海,康毅力,等. 天然裂缝性地层钻井液漏失规律研究[J]. 西南石油大学学报(自然科学版),2016,38(3):101–106. LI Daqi, LIU Sihai, KANG Yili, et al. Dynamic behavior of drilling fluid leakage in naturally fractured formations[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2016, 38(3): 101–106.
[16] 贾利春,陈勉,侯冰,等. 裂缝性地层钻井液漏失模型及漏失规律[J]. 石油勘探与开发,2014,41(1):95–101. doi: 10.11698/PED.2014.01.12 JIA Lichun, CHEN Mian, HOU Bing, et al. Drilling fluid loss model and loss dynamic behavior in fractured formations[J]. Petroleum Exploration and Development, 2014, 41(1): 95–101. doi: 10.11698/PED.2014.01.12
[17] OZDEMIRTAS M, KURU E, BABADAGLI T. Experimental investigation of borehole ballooning due to flow of non-Newtonian fluids into fractured rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(7): 1200–1206. doi: 10.1016/j.ijrmms.2010.07.002
[18] 王明波,郭亚亮,方明君,等. 裂缝性地层钻井液漏失动力学模拟及规律[J]. 石油学报,2017,38(5):597–606. doi: 10.7623/syxb201705013 WANG Mingbo, GUO Yaliang, FANG Mingjun, et al. Dynamics simulation and laws of drilling fluid loss in fractured formations[J]. Acta Petrolei Sinica, 2017, 38(5): 597–606. doi: 10.7623/syxb201705013
[19] 李大奇. 裂缝性地层钻井液漏失动力学研究[D]. 成都:西南石油大学,2012. LI Daqi. Numerical and experimental investigations of drilling fluid losses in fractured formations[D]. Chengdu: Southwest Petroleum University, 2012.
[20] 牛骏,苏建政,严侠,等. 基于嵌入式离散裂缝和扩展有限元的裂缝性页岩油藏流固耦合高效数值模拟方法[J]. 科学技术与工程,2020,20(7):2643–2651. doi: 10.3969/j.issn.1671-1815.2020.07.017 NIU Jun, SU Jianzheng, YAN Xia, et al. An efficient numerical simulation method with hydro-mechanical coupling model of fractured shale oil reservoir based on embedded discrete fracture model and extended finite element method[J]. Science Technology and Engineering, 2020, 20(7): 2643–2651. doi: 10.3969/j.issn.1671-1815.2020.07.017
[21] 陈志明,张绍琦,周彪,等. 考虑离散裂缝的非均质裂缝性气藏数值试井新模型[J]. 天然气工业,2023,43(2):77–86. doi: 10.3787/j.issn.1000-0976.2023.02.008 CHEN Zhiming, ZHANG Shaoqi, ZHOU Biao, et al. A new numerical well testing model considering discrete fractures for heterogeneous fractured gas reservoirs[J]. Natural Gas Industry, 2023, 43(2): 77–86. doi: 10.3787/j.issn.1000-0976.2023.02.008
[22] 金泰宇. 三维粗糙裂缝网络钻井液漏失流固耦合模型研究[J]. 石油钻探技术,2024,52(1):69–77. doi: 10.11911/syztjs.2023100 JIN Taiyu. Study on three-dimensional fluid-solid coupling model of drilling fluid leakage in rough fracture network[J]. Petroleum Drilling Techniques, 2024, 52(1): 69–77. doi: 10.11911/syztjs.2023100
[23] 房娜,刘宗宾,岳宝林,等. 裂缝性油藏渗流特征及注水策略[J]. 特种油气藏,2024,31(3):91–97. doi: 10.3969/j.issn.1006-6535.2024.03.012 FANG Na, LIU Zongbin, YUE Baolin, et al. Seepage characteristics and water injection strategy of fractured reservoir[J]. Special Oil & Gas Reservoirs, 2024, 31(3): 91–97. doi: 10.3969/j.issn.1006-6535.2024.03.012
[24] PENG Yan, LIU Jishan, PAN Zhejun, et al. A sequential model of shale gas transport under the influence of fully coupled multiple processes[J]. Journal of Natural Gas Science and Engineering, 2015, 27(Part 2): 808-821.
[25] 高永海. 深水油气钻探井筒多相流动与井控的研究[D]. 青岛:中国石油大学(华东),2007. GAO Yonghai. Study on multi-phase flow in wellbore and well control in deep water drilling[D]. Qingdao: China University of Petroleum(East China), 2007.
[26] 李宁,刘洪涛,张权,等. 大温压域钻井液流变参数预测模型[J]. 钻井液与完井液,2023,40(2):143–155. doi: 10.12358/j.issn.1001-5620.2023.02.001 LI Ning, LIU Hongtao, ZHANG Quan, et al. Model for predicting drilling fluid rheological parameters in wide temperature and pressure range[J]. Drilling Fluid & Completion Fluid, 2023, 40(2): 143–155. doi: 10.12358/j.issn.1001-5620.2023.02.001
[27] WEI Shiming, JIN Yan, XIA Yang. Predict the mud loss in natural fractured vuggy reservoir using discrete fracture and discrete vug network model[J]. Journal of Petroleum Science and Engineering, 2020, 195: 107626. doi: 10.1016/j.petrol.2020.107626
[28] LIAO Youqiang, WANG Zhiyuan, CHAO Mingzhe, et al. Coupled wellbore–reservoir heat and mass transfer model for horizontal drilling through hydrate reservoir and application in wellbore stability analysis[J]. Journal of Natural Gas Science and Engineering, 2021, 95: 104216. doi: 10.1016/j.jngse.2021.104216
[29] 黄朝琴,高博,王月英,等. 基于模拟有限差分法的离散裂缝模型两相流动模拟[J]. 中国石油大学学报(自然科学版),2014,38(6):97–105. doi: 10.3969/j.issn.1673-5005.2014.06.015 HUANG Zhaoqin, GAO Bo, WANG Yueying, et al. Two-phase flow simulation of discrete fracture model using a novel mimetic finite difference method[J]. Journal of China University of Petroleum (Edition of Natural Science), 2014, 38(6): 97–105. doi: 10.3969/j.issn.1673-5005.2014.06.015
[30] YAN Xia, HUANG Zhaoqin, YAO Jun, et al. An efficient numerical hybrid model for multiphase flow in deformable fractured-shale reservoirs[J]. SPE Journal, 2018, 23(4): 1412–1437. doi: 10.2118/191122-PA
[31] LIU Jia, XUE Yi, ZHANG Qi, et al. Coupled thermo-hydro-mechanical modelling for geothermal doublet system with 3D fractal fracture[J]. Applied Thermal Engineering, 2022, 200: 117716. doi: 10.1016/j.applthermaleng.2021.117716
[32] 滕学清,孙宝江,张耀明,等. 无安全压力窗口裂缝性地层五步压回法压井方法[J]. 石油钻探技术,2018,46(6):20–25. TENG Xueqing, SUN Baojiang, ZHANG Yaoming, et al. A five-step bullheading killing well control method for fractured formations without a safety pressure window[J]. Petroleum Drilling Techniques, 2018, 46(6): 20–25.
[33] 张磊,许杰,谢涛,等. 几种裂缝性漏失压力计算模型的比较分析[J]. 石油机械,2018,46(9):13–17. ZHANG Lei, XU Jie, XIE Tao, et al. Comparison of several calculation models for loss pressure of fractured formation[J]. China Petroleum Machinery, 2018, 46(9): 13–17.
[34] 金衍,陈勉,刘晓明,等. 塔中奥陶系碳酸盐岩地层漏失压力统计分析[J]. 石油钻采工艺,2007,29(5):82–84. doi: 10.3969/j.issn.1000-7393.2007.05.023 JIN Yan, CHEN Mian, LIU Xiaoming, et al. Statistic analysis of leakage pressure of Ordovician carbonate formation in middle Tarim Basin[J]. Oil Drilling & Production Technology, 2007, 29(5): 82–84. doi: 10.3969/j.issn.1000-7393.2007.05.023
-
期刊类型引用(1)
1. 周元龙, 赵淑霞, 何应付, 王锐. 基于响应面方法的CO_2重力稳定驱油藏优选. 断块油气田. 2019(06): 761-765 . 
百度学术
其他类型引用(0)
下载:
计量
- 文章访问数: 14
- HTML全文浏览量: 6
- PDF下载量: 8
- 被引次数: 1
