基于邻井距离测量误差的救援井磁测距工具优选方法

于瑞丰; 刁斌斌; 高德利

doi:10.11911/syztjs.2021129

基于邻井距离测量误差的救援井磁测距工具优选方法

石油工程教育部重点实验室（中国石油大学（北京）），北京 102249

基金项目: 国家自然科学基金重点项目“页岩和致密油气田高效开发建井基础研究”（编号：U1762214）、国家自然科学基金创新研究群体项目“复杂油气井钻井与完井基础研究”（编号：51821092）联合资助

详细信息

作者简介:
于瑞丰（1993—），男，河南南阳人，2015年毕业于长江大学石油工程专业，2018年获中国石油大学（北京）油气井工程专业硕士学位，在读博士研究生，主要从事油气井力学与控制工程研究。E-mail：2020310123@student.cup.edu.cn

中图分类号: TE32⁺8
计量
- 文章访问数: 660
- HTML全文浏览量: 284
- PDF下载量: 65
出版历程
- 收稿日期: 2021-04-11
- 修回日期: 2021-08-16
- 网络出版日期: 2021-09-08
- 刊出日期: 2021-11-24

Optimal Selection Method of Magnetic Ranging Tools for Relief Well Engineering Based on the Measurement Error of the Adjacent Well Distance

MOE Key Laboratory of Petroleum Engineering, China University of Petroleum(Beijing), Beijing, 102249, China

摘要

摘要: 为了确保能在可探测的前提下选用测量精度更高、作业风险更小的磁测距工具探测事故井，进行了救援井与事故井相对距离测量误差计算。由于“梯形”误差模型无法与井眼轨迹误差相耦合，通过协方差传播率，建立了磁测距工具测量误差模型。将磁测距工具测量误差与井眼轨迹误差相耦合，可得到磁测距工具工作平面内的总协方差矩阵，进而给出由总协方差矩阵确定的误差椭圆和救援井磁测距工具的优选方法。实例计算结果显示，救援井当前井底与事故井相距7.41 m时，磁测距工具测量误差椭圆长、短半轴长度分别为1.26 m和0.33 m。测距作业后，救援井继续钻进，当两井相对距离为6.68 m时，推荐使用Wellspot工具；当两井相对距离为5.21 m或2.07 m时，推荐使用RGRⅠ工具。研究结果表明，测距作业后，随着救援井继续钻进，两井相对距离的减小趋势大于两井相对距离测量误差的增大趋势；当磁测距工具探测范围完全包覆两井相对距离测量误差椭圆时，可以选用作业距离更小、但测量精度更高的磁测距工具。
- 救援井 /
- 相对距离 /
- 测量误差 /
- 磁测距工具 /
- 工具优选
Abstract: Measurement errors of the relative distance from an accident well to its relief well were calculated from magnetic ranging tools with higher measurement accuracy and lower operational risks on the premise that the accident well was within the tools’ detection ranges. As the error calculated by the “trapezoidal” error model could not be coupled with the wellbore trajectory error, a measurement error model for magnetic ranging tools was built through the covariance propagation rate. The measurement errors of magnetic ranging tools were coupled with the wellbore trajectory errors to obtain the total covariance matrixes in the working planes of the magnetic ranging tools. The error ellipses and the optimal selection method of magnetic ranging tools for the relief well were thereby derived. The example calculation showed that when the current bottom of the relief well was 7.41 m away from the accident well, the semi-axis lengths of the measurement error ellipses were 1.26 m and 0.33 m. After the ranging operation, the relief well drilling continued to drill. The wellspot tool or RGR-I tool were recommended when the relative distance between the two wells was 6.68 m or was shortened to 5.21 m and then to 2.07 m, respectively. The research results show that the decreasing trend of the relative distance between the two wells is greater than the increasing trend of the measurement error of the relative distance after the range measuring operations and as relief well drilling continues. When the detection range of a magnetic ranging tool fully covers the measurement error ellipse of the relative distance between the two wells, magnetic ranging tools with shorter measurement ranges but higher accuracy can be used.
- relief well /
- relative distance /
- measurement error /
- magnetic ranging tools /
- tool selection

HTML全文

油气井发生严重井喷事故后，往往难以对事故井进行有效控制，一般采用救援井连通事故井的方式实施压井作业控制事故井。由于传统测斜工具存在累积误差，在实际救援井作业中需要使用磁测距工具直接探测其与事故井的距离，进而引导救援井与事故井在设计连通点连通^[1-2]。目前投入商业应用的只有基于注入电流法的WellspotTM系列工具；为了打破垄断，近年来我国开展了磁测距工具工作原理相关研究，并建立了磁测距工具计算模型^[3-11]。由于不同磁测距工具之间性能指标和工艺流程差异很大，在救援井钻井过程中往往需要使用多种磁测距工具。在不多的救援井实例报道中，国外学者往往只简要给出在救援井不同作业阶段测距所采用的工具而没有就更换磁测距工具原因给出明确的解释^[12]。关于救援井钻井过程中磁测距工具的选用，国内外目前主要集中在初始测距点处，而对于后续测距作业鲜有涉及^[13]。这是因为，在初始测距点执行磁测距作业后，救援井继续钻进一定距离，此时救援井当前井底与事故井的相对距离测量误差由两井井眼轨迹误差转变为由磁测距工具测量误差与井眼轨迹误差共同决定。针对井眼轨迹误差，国内外已经发展形成了以ISCWSA-MWD和WdW误差模型为代表的一系列研究成果^[14-17]。而对于主动磁测距工具测量误差引起的不确定区域，国内外学者往往将其简单近似为梯形，这种方法虽然直观、简单，但也存在无法定量描述测点落在特定区域内的概率，及无法与井眼轨迹误差相耦合的缺点^[15，18]。为了克服上述“梯形”模型的缺点，建立了基于协方差传播率的磁测距工具测量误差模型，以协方差矩阵的形式定量描述磁测距工具的测量误差；将代表磁测距工具测量误差与井眼轨迹误差的协方差矩阵相加，实现了救援井与事故井相对距离测量误差的定量计算。给定置信因子及磁测距工具测量平面，可通过协方差矩阵进一步确定两井相对距离测量误差在该平面内的误差椭圆。最终通过对比该误差椭圆与磁测距工具探测范围的空间关系，给出了救援井磁测距工具的优选方法。

1. 相对距离测量误差组成分析

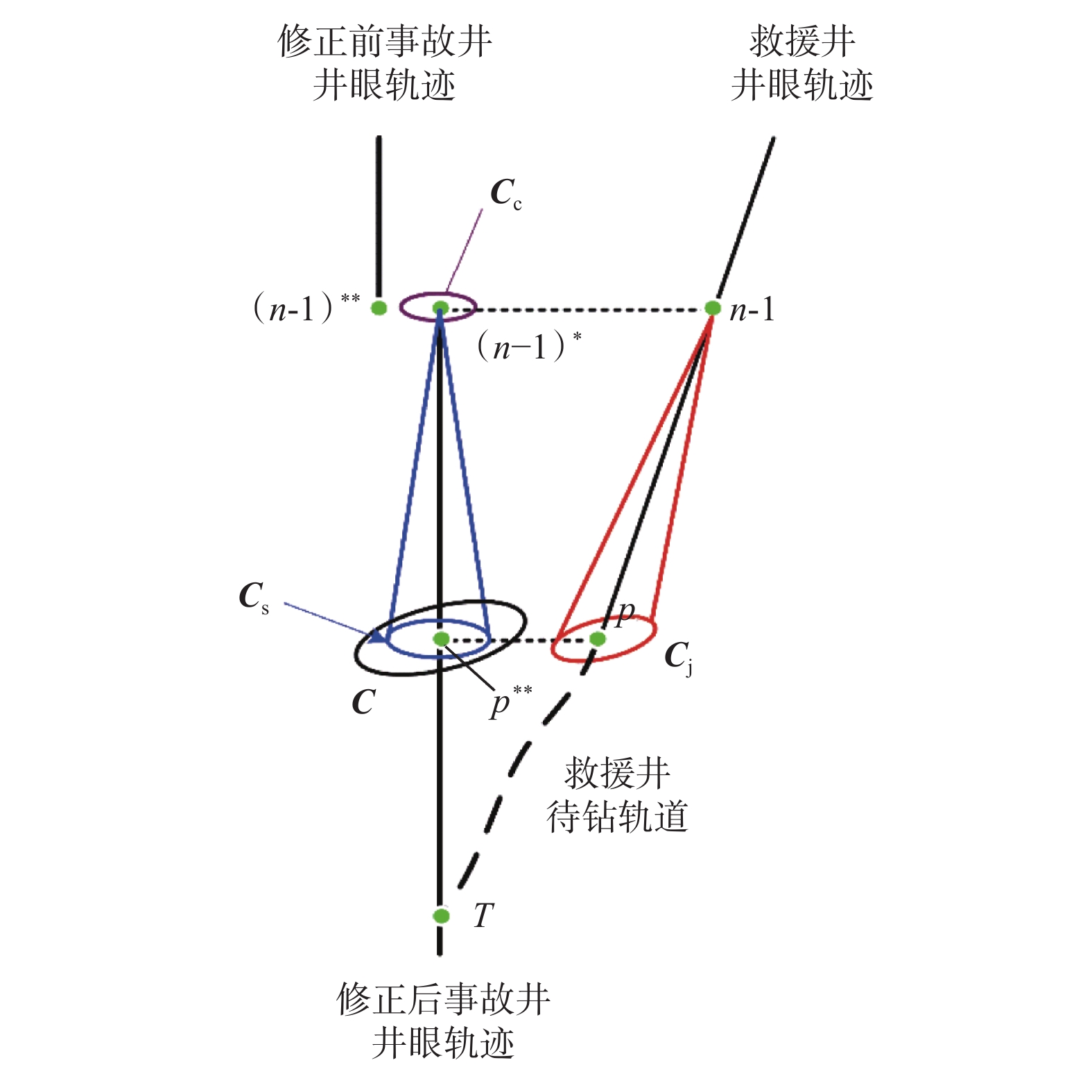
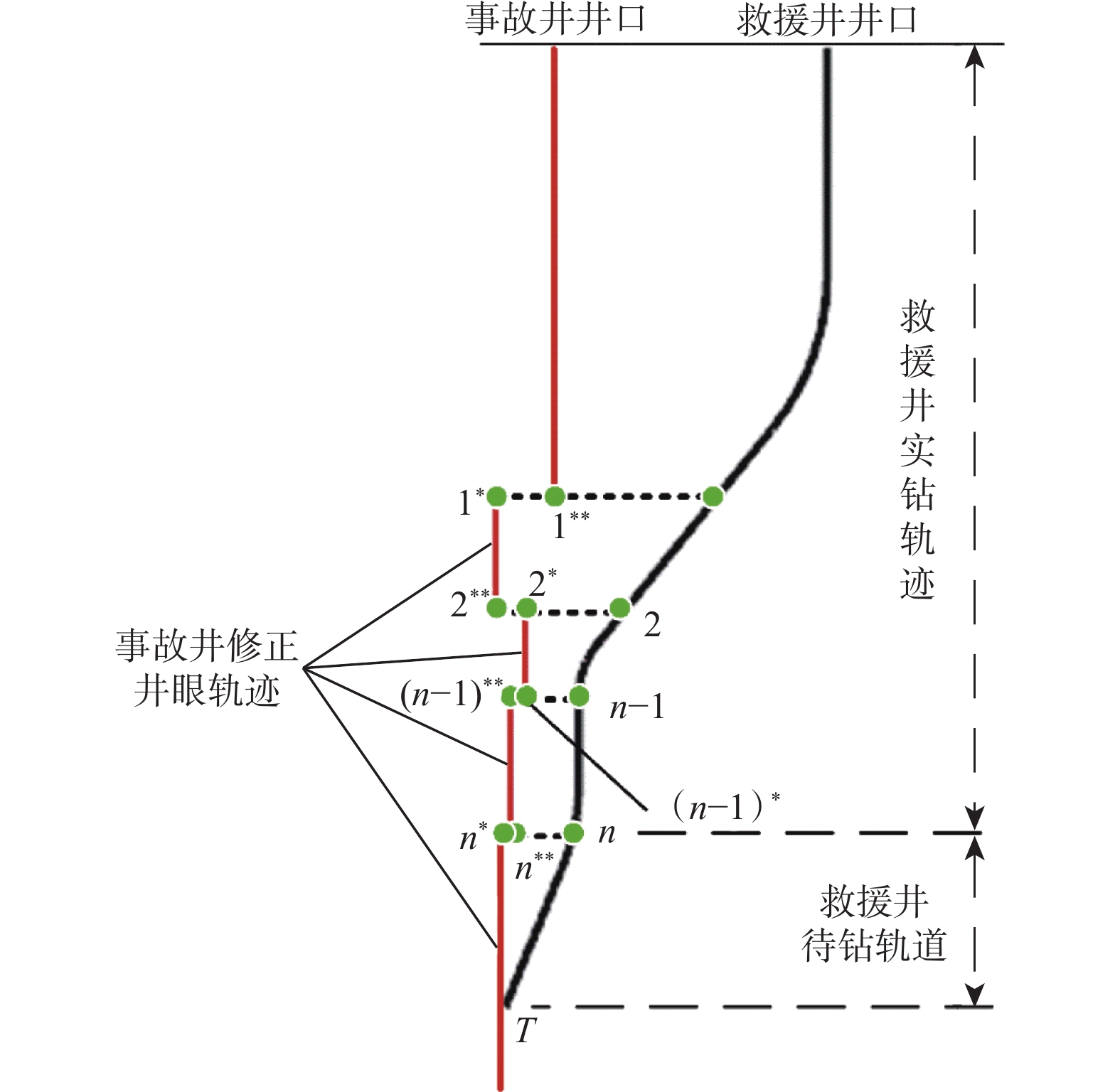
由于磁测距工具的探测范围有限且每次测距作业都需要占用大量的作业时间，救援井施工是一个联合使用磁测距工具与测斜仪器逐步引导救援井钻进的过程，引导过程如图1所示。图1中，点1，2，…，n、点1^*，2^*，…，n^*和点1^**，2^**，…，n^**为对应的测点。其中，点1，2，…，n为测距作业时救援井当前井底，点1^*，2^*，…，n^*为实测事故井相对位置，点1^**，2^**，…，n^**为使用历史测斜数据计算得到的事故井预测测点。由于测斜仪器与磁测距工具均存在测量误差且误差精度不同，点1^*，2^*，…，n^*和点1^**，2^**，…，n^**不重合。T为第n次测距后预测的连通点位置。每次测距作业后都需要以事故井实测点为基准对事故井井眼轨迹进行修正，并以修正后的点T为靶点重新进行待钻井眼轨道设计^[19]。随着钻进的进行，两井距离越来越近，磁测距工具精度越来越高，事故井预测测点与实测测点相差越来越小。当救援井与事故井足够靠近时，预测连通点T与实际连通点会非常接近甚至重叠，此时继续钻进，两井大概率实现连通。

图 1 磁测距工具引导两井连通过程示意

Figure 1. Connection process of two wells via magnetic ranging tools

下载: 全尺寸图片幻灯片

根据磁测距工具引导救援井钻进过程，可以得到磁测距作业后两井相对距离测量误差的组成，如图2所示（图2中，点(n–1)^*为上一次测距作业实测测点，点p为救援井当前井底，点p**为事故井上与点p对应的预测测点）。测距作业后以实测测点(n–1)^*代替点(n–1)**对事故井井眼轨迹进行修正，修正后测点以深事故井井眼轨迹为事故井相对于救援井的井眼轨迹。由图2可知，预测测点p**相对于点n–1的相对距离测量误差由3部分组成：点(n–1)^*相对于点n–1的测量误差、点p**相对点(n–1)^*的测量误差和点p相对于点n–1的测量误差。

图 2 两井相对距离测量误差

Figure 2. Measurement error of the relative distance between the two wells

下载: 全尺寸图片幻灯片

因此，点p^**相对于点n–1的相对距离测量误差总协方差矩阵可表示为^[20]：

${\boldsymbol{C}}{\text{ = }}{{\boldsymbol{C}}_{\text{j}}}{\text{ + }}{{\boldsymbol{C}}_{\text{s}}}{\text{ + }}{{\boldsymbol{C}}_{\text{c}}}$

(1)

式中：C_s，C_j分别为点p^**相对于点(n–1)^*和点p相对于点n–1的井眼轨迹测量误差，用协方差矩阵表示，m²；C_c为点(n–1)^*相对于点n–1的磁测距工具测量误差，用协方差矩阵表示，m²。

2. 相对距离测量误差计算

2.1 坐标系的建立及相对位置计算

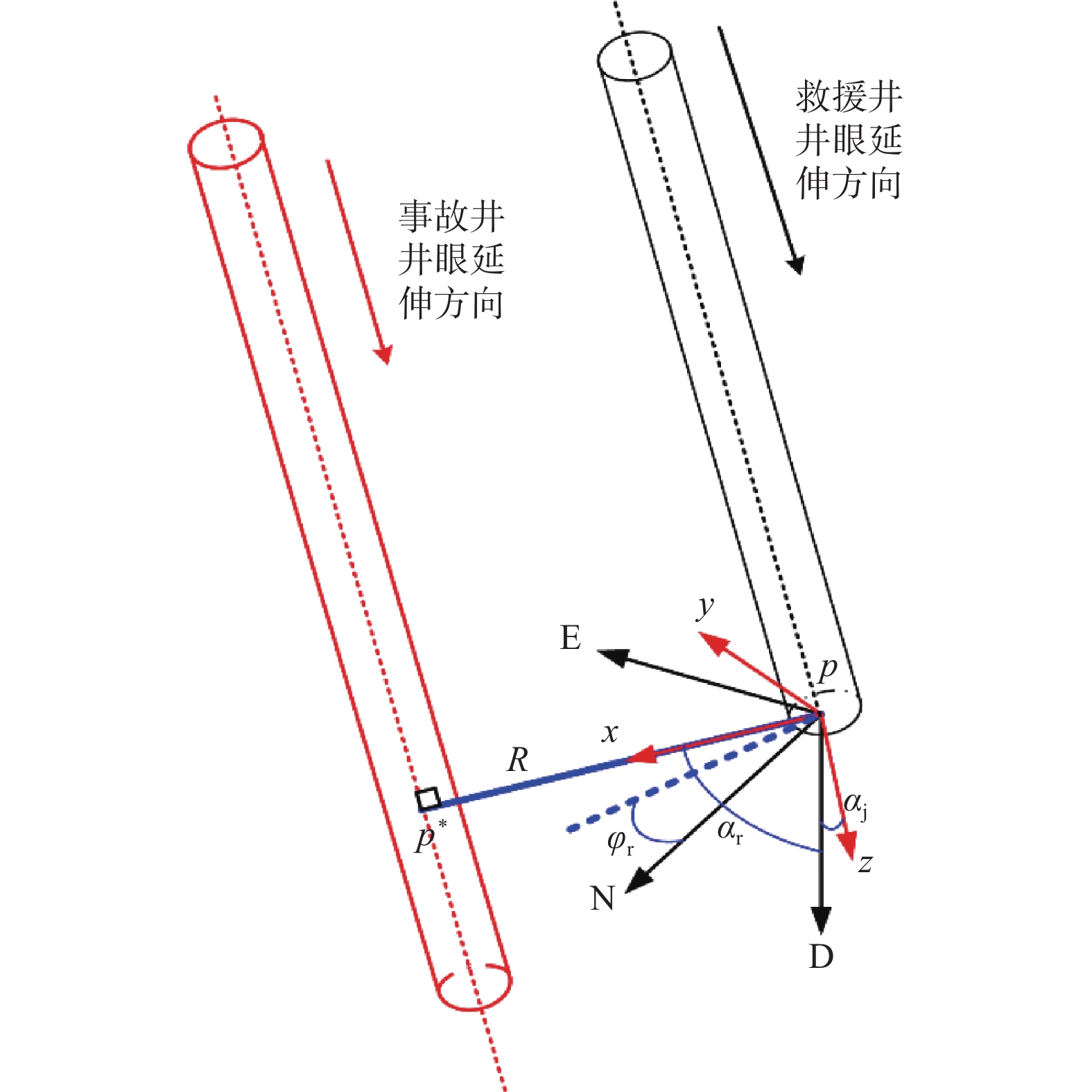
磁测距作业时，共建立2个坐标系（见图3）。以救援井当前井底p为原点，建立大地坐标系p-NED，N轴指向磁北，E轴指向正东，D轴铅锤向下指向地心。以救援井当前井底p为原点，建立右手直角坐标系p-xyz，z轴指向救援井测点p处井眼延伸方向，x轴由点p指向点p^*，y轴由右手定则确定。

图 3 磁测距作业时建立的坐标系示意

Figure 3. Diagram of the established coordinate systems

下载: 全尺寸图片幻灯片

主动磁测距工具所测量的数据为测点p^*在坐标系p-NED中的相对位置p^*（R，α_r，φ_r）。由于目前已钻救援井案例在进行磁测距作业时事故井测段均为垂直井段或救援井与事故井近似平行，且主动磁测距工具测量相对距离为测点p至事故井井段的最近距离^[21]，可知此时相对仰角α_r为90°或（90°+α_j）。在p-NED坐标系中，利用式（2）将工具测得的极坐标参数p^*（R，α_r，φ_r）换算为坐标参数：

$\left\{ {\begin{array}{*{20}{l}} {{N_{{{{p}}^ * }}} = R{\rm{sin}}\;{\alpha _{\rm{r}}}\cos {\varphi _{\rm{r}}}} \\ {{E_{{{{p}}^ * }}} = R\sin\; {\alpha _{\rm{r}}}\sin {\varphi _{\rm{r}}}} \\ {{D_{{{{p}}^ * }}} = R\cos \;{\alpha _{\rm{r}}}} \end{array}} \right.$

(2)

式中：R为相对距离，m；φ_r为相对方位角，（°）；α_r为相对仰角，（°）；α_j为救援井当前井底的井斜角，（°）；N_p*，E_p*和D_p*分别为点p^*在坐标系p-NED内的坐标，m。

坐标系p-xyz与p-NED的转换矩阵为：

${{\boldsymbol{T}}_{{p}}} = \left[ {\begin{array}{*{20}{c}} {\cos\; {\alpha _{\rm{r}}}\cos\; {\varphi _{\rm{r}}}}&{\cos\; {\alpha _{\rm{r}}}{\rm{sin}}\;{\varphi _{\rm{r}}}}&{ - \sin\; {\alpha _{\rm{r}}}} \\ { - \sin \;{\varphi _{\rm{r}}}}&{\cos\; {\varphi _{\rm{r}}}}&0 \\ {\sin\; {\alpha _{\rm{r}}}\cos\; {\varphi _{\rm{r}}}}&{\sin\; {\alpha _{\rm{r}}}\sin\; {\varphi _{\rm{r}}}}&{\cos\; {\alpha _{\rm{r}}}} \end{array}} \right]$

(3)

2.2 主动磁测距工具测量误差计算

主动磁测距工具的测量原理是，通过井下电极向地层中注入高频、低频交流电，从而在事故井上聚集形成沿套管和钻杆向上、向下流动的交变电流。根据安培定则，此电流会在事故井周围产生交变磁场。通过探管测量该交变磁场并将测量数据传输至地面，在地面对测量数据进行处理可得到探管到套管的相对距离和相对方位^[22]。通常认为，主动磁测距工具误差源为相对方位角与相对距离，误差源精度通常以极限误差形式给出。为了便于计算，需要将误差源精度换算为标准差。假设误差源相互独立，测点p^*位置分布满足正态分布。根据随机误差协方差传播率^[23]，可根据式（4）—式（7）确定在坐标系p-NED内点p^*相对于点p的磁测距工具测量误差的协方差矩阵C_c：

${{\boldsymbol{C}}_{\rm{c}}} = {\boldsymbol{KD}}{{\boldsymbol{K}}^{\rm{T}}}$

(4)

${\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {\sigma _R^2}&{} \\ {}&{\sigma _{{\varphi _{\rm{r}}}}^2} \end{array}} \right]$

(5)

式中：σ_φ_r为相对方位角测量误差的标准差，（°）；σ_R为相对距离测量误差的标准差，m。

${\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {{\rm{sin}}\;{\alpha _{\rm{r}}}\cos\; {\varphi _{\rm{r}}}} \\ {\sin\; {\alpha _{\rm{r}}}\sin\; {\varphi _{\rm{r}}}} \\ {\cos\; {\alpha _{\rm{r}}}} \end{array}\begin{array}{*{20}{c}} { - R{\rm{sin}}\;{\alpha _{\rm{r}}}\sin\; {\varphi _{\rm{r}}}} \\ {R\sin\; {\alpha _{\rm{r}}}\cos\; {\varphi _{\rm{r}}}} \\ 0 \end{array}} \right]$

(6)

在p-xyz坐标系中，表示点p*相对于点p的磁测距工具测量误差的协方差矩阵H_c为：

${{\boldsymbol{H}}_{\rm{c}}} = {{\boldsymbol{T}}_{{p}}}{{\boldsymbol{C}}_{\rm{c}}}{\boldsymbol{T}}_{{P}}^{\rm{T}}$

(7)

2.3 误差椭圆

根据主动磁测距工具的工作原理可知，工具的探测范围为p-xy平面内以p为圆心、以探测距离r为半径的圆。为便于分析，将C通过转换矩阵转换到坐标系p-xyz中，则在p-xyz中点p**相对于点n–1的相对距离测量误差的协方差矩阵H可表示为：

${\boldsymbol{H}} = {{\boldsymbol{T}}_{{p}}}{\boldsymbol{CT}}_{{P}}^{\rm{T}}$

(8)

将协方差矩阵H分块，可得到误差椭圆在p-xy平面的截面方程^[24-25]：

${\left[ {\begin{array}{*{20}{c}} {\Delta x} \\ {\Delta y} \end{array}} \right]^{\rm{T}}}{\left[ {\begin{array}{*{20}{c}} {\sigma _x^2}&{{\sigma _{xy}}} \\ {{\sigma _{yx}}}&{\sigma _y^2} \end{array}} \right]^{{\rm{ - }}1}}\left[ {\begin{array}{*{20}{c}} {\Delta x} \\ {\Delta y} \end{array}} \right] = {k^2}$

(9)

式中：k为置信因子，通常取3.41时的置信水平为99.7%；σ_xy为x、y坐标间的协方差，m²；σ_x²，σ_y²分别为x、y坐标的方差，m²。

协方差矩阵可通过式（10）进行分解：

$\left[ {\begin{array}{*{20}{c}} {\sigma _x^2}&{{\sigma _{xy}}} \\ {{\sigma _{yx}}}&{\sigma _y^2} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\;\theta }&{ - \sin \;\theta } \\ {\sin\; \theta }&{{\rm{cos}}\;\theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\lambda _1}}&0 \\ 0&{{\lambda _2}} \end{array}} \right] {\left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\;\theta }&{ - \sin\;\theta } \\ {\sin \;\theta }&{{\rm{cos}}\;\theta } \end{array}} \right]^{\rm{T}}}$

(10)

在p-xy坐标系中，测点p**相对于点n–1的不确定范围为p-xy平面上的误差椭圆，则：

${r_{\rm{1}}} = k\sqrt {{\lambda _{\rm{1}}}}$

(11)

${r_{\rm{2}}} = k\sqrt {{\lambda _{\rm{2}}}}$

(12)

式中：θ为椭圆旋转角度，（°）；r₁，r₂分别为椭圆长、短半径，m；λ₁，λ₂为矩阵特征值，m²。

已知旋转角度θ和椭圆旋转中心p**在p-xy平面内，可由标准椭圆旋转、平移后得到两井相对距离测量误差的误差椭圆。

3. 主动磁测距工具优选方法

3.1 主动磁测距工具分析

目前，现场应用最多的主动磁测距工具是基于注入电流法的Wellspot^TM 系列工具，包括标准Wellspot、RGR Ⅰ和WSAB，其主要性能指标见表1^[12]。

表 1 主动电磁测距工具性能指标

Table 1. Performance indexes of active electromagnetic ranging tools

测距工具	探测范围/m	距离精度，%	方位精度/（°）	外径/mm	温度/℃	压力/MPa	备注
Wellspot	61.0	±20	±3	50.8	204.4	172.4	每次测距需要起下钻
WSAB	4.6	±20	±3	215.9	125.0	103.4	不需要起下钻
WSAB	2.1	±5	±3	50.8	125.0	103.4	不需要起下钻
RGRⅠ	7.6	±5	±3	114.3	176.6	137.9

下载: 导出CSV

| 显示表格

由表1可知，不同磁测距工具之间的性能指标和工艺流程差异很大。若选用的磁测距工具探测范围过大，虽然可以探测到事故井，但测量误差较大，不利于两井实现最终连通；若选用的磁测距工具探测范围过小，很有可能无法一次探测到事故井，起钻更换磁测距工具会浪费作业时间和增加作业风险。因此，救援井作业过程中需要根据两井距离关系选用合适的磁测距工具。

3.2 主动磁测距工具的优选方法

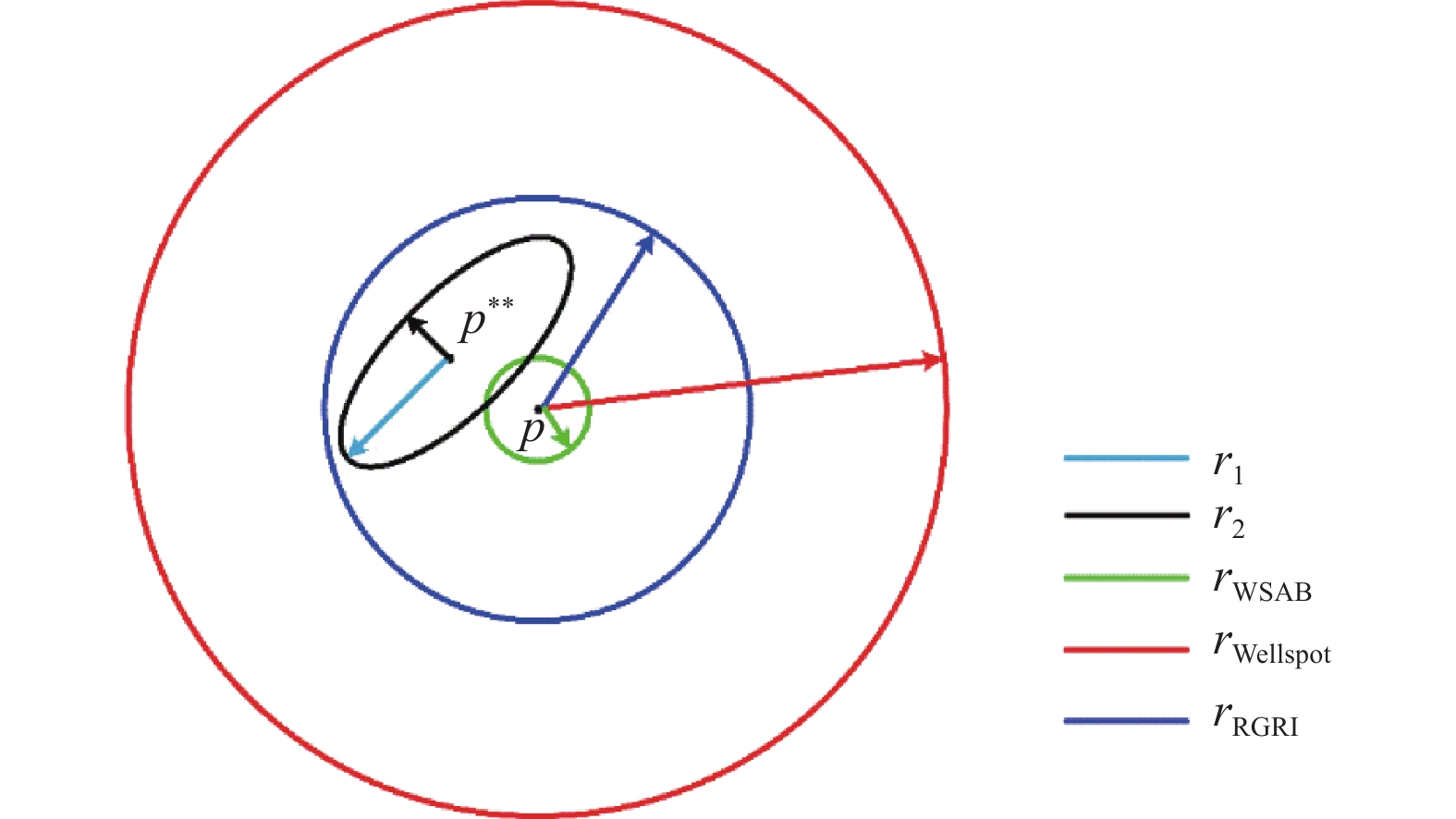
通过p-xy平面内的两井相对距离测量误差椭圆与主动磁测距工具探测范围的空间关系来选择主动磁测距工具，主动磁测距工具的优选方法如图4所示（图4中，r_Wellspot为Wellspot工具最大探测范围，m；r_RGRⅠ为RGRⅠ工具最大探测范围，m；r_WSAB为WSAB工具最大探测范围，m）。

图 4 主动电磁测距工具优选方法

Figure 4. Optimal selection method of active electromagnetic ranging tools

下载: 全尺寸图片幻灯片

具体判别方式：1）当只有Wellspot工具探测范围完全包覆合成误差椭圆时，使用Wellspot工具；2）当Wellspot工具与RGRⅠ工具探测范围能完全包覆合成误差椭圆、且WSAB工具的探测范围无法完全包覆合成误差椭圆时，考虑测量精度，使用RGRⅠ工具；3）当3种磁测距工具探测范围均可完全包覆合成误差椭圆时，考虑测量精度及井下安全，使用WSAB工具。

4. 算例分析

4.1 基础数据

假定事故井为直井，套管下深6 131 m。救援井井口位于事故井井口北偏东60°方向，井口距离500 m。设计连通点T垂深为5 831.2 m，连通点位于套管上。当地磁偏角δ=4.0°，磁倾角β=72°，地磁场强度B=50 000 nT。

救援井点1处使用Wellspot工具进行了一次测距作业，成功探测到了事故井，事故井测点1^*在1-NED坐标系中的球坐标为（7.41，240°，90°），直角坐标为（0.15，0.13，0）。以1*作为初始点更新事故井井眼轨迹，并重新进行待钻轨道设计。测距作业后，使用测斜仪器对两井相对距离进行监测，并顺序钻进至点2、3、4处，设计在点2、3、4处分别使用主动磁测距工具进行测距作业。使用历史测斜数据，计算得到了事故井预测测点2^**、3^**、4^**。

在1-NED坐标系中，根据ISCWSA模型计算井眼轨迹误差的协方差矩阵如下：

$\begin{array}{l} {{\boldsymbol{C}}_{{\rm{j12}}}} = \left[ {\begin{array}{*{20}{c}} {2.18{{\times 10}^{ - 3}}}&{3.18{{\times 10}^{ - 7}}}&{1.09{{\times 10}^{ - 4}}}\\ {3.18{{\times 10}^{ - 7}}}&{2.75{{\times 10}^{ - 4}}}&{1.{\rm{67}}{{\times 10}^{ - 8}}}\\ {1.09{{\times 10}^{ - 5}}}&{1.{\rm{67}}{{\times 10}^{ - 8}}}&{1.{\rm{18}}{{\times 10}^{ - 5}}} \end{array}} \right]\\ {{\boldsymbol{C}}_{{\rm{j13}}}} = \left[ {\begin{array}{*{20}{c}} {2.{\rm{18}}{{\times 10}^{ - 3}}}&{3.{\rm{16}}{{\times 10}^{ - 6}}}&{1.{\rm{09}}{{\times 10}^{ - 4}}}\\ {3.{\rm{16}}{{\times 10}^{ - 6}}}&{2.{\rm{73}}{{\times 10}^{ - 3}}}&{1.{\rm{66}}{{\times 10}^{ - 7}}}\\ {1.{\rm{09}}{{\times 10}^{ - 4}}}&{1.{\rm{66}}{{\times 10}^{ - 7}}}&{1.{\rm{07}}{{\times 10}^{ - 4}}} \end{array}} \right]\\ {{\boldsymbol{C}}_{{\rm{j14}}}} = \left[ {\begin{array}{*{20}{c}} {1.{\rm{32}}{{\times 10}^{ - 2}}}&{1.{\rm{92}}{{\times 10}^{ - 5}}}&{6.{\rm{60}}{{\times 10}^{ - 4}}}\\ {1.{\rm{92}}{{\times 10}^{ - 5}}}&{1.{\rm{66}}{{\times 10}^{ - 2}}}&{1.{\rm{01}}{{\times 10}^{ - 6}}}\\ {6.{\rm{60}}{{\times 10}^{ - 4}}}&{1.{\rm{01}}{{\times 10}^{ - 6}}}&{{\rm{6}}{\rm{.39}}{{\times 10}^{ - 4}}} \end{array}} \right] \end{array}$

$\begin{array}{l} {{\boldsymbol{C}}_{{\rm{s1^*2^{**}}}}} = \left[ {\begin{array}{*{20}{c}} {2.13{{\times 10}^{ - 4}}}&{}&{}\\ {}&{2.13{{\times 10}^{ - 4}}}&{}\\ {}&{}&{1.13{{\times 10}^{ - 5}}} \end{array}} \right]\\ {{\boldsymbol{C}}_{{\rm{s1^*3^{**}}}}} = \left[ {\begin{array}{*{20}{c}} {2.{\rm{12}}{{\times 10}^{ - 3}}}&{}&{}\\ {}&{2.{\rm{12}}{{\times 10}^{ - 3}}}&{}\\ {}&{}&{1.{\rm{02}}{{\times 10}^{ - 4}}} \end{array}} \right]\\ {{\boldsymbol{C}}_{{\rm{s1^*4^{**}}}}} = \left[ {\begin{array}{*{20}{c}} {1.{\rm{28}}{{\times 10}^{ - 2}}}&{}&{}\\ {}&{1.{\rm{28}}{{\times 10}^{ - 2}}}&{}\\ {}&{}&{6.{\rm{03}}{{\times 10}^{ - 4}}} \end{array}} \right] \end{array}$

4.2 计算与分析

由于事故井为直井，因此主动磁测距工具探测平面1-xy与1-NE共面。在1-NE平面内求得事故井测点1^*相对于点1的测量误差协方差矩阵：

${{\boldsymbol{C}}_{{\rm{c11^*}}}} = \left[ {\begin{array}{*{20}{c}} {4.14{\times 10^{ - 2}}}&{5.{\rm{54}}{\times 10^{ - 2}}}&0 \\ {5.{\rm{54}}{\times 10^{ - 2}}}&{1.05{\times 10^{ - 2}}}&0 \\ 0&0&0 \end{array}} \right]$

取置信因子k=3.41，由协方差矩阵计算误差椭圆长、短半轴长度分别为1.26 m和0.33 m。在1-NE平面内绘制1*相对于点1的位置不确定性误差椭圆，如图5所示。由图5可知，根据协方差矩阵绘制的误差椭圆在梯形区域内。这是因为，误差椭圆只表示一定置信区间内的位置分布可能性，而梯形方法则表示所有测点可能分布的区域。误差椭圆置信区间为99.7%，则测点落在2种方法未相交区域的可能性仅为0.3%，因此可以使用该误差模型计算主动磁测距工具测量误差。

图 5 主动磁测距工具测量误差示意

Figure 5. Measurement error of active magnetic ranging tools

下载: 全尺寸图片幻灯片

根据几何关系及相对位置不确定性分析，可得在设计的不同测点处两井相对距离测量误差椭圆的长、短半径（见表2）。

表 2 预测测点处两井相对距离测量误差椭圆

Table 2. Predicted measurement error ellipses of the relative distances between the two wells at the ranging points

设计测点	设计测点坐标		预测相对距离/m	误差椭圆半径/m		旋转角θ/ （°）
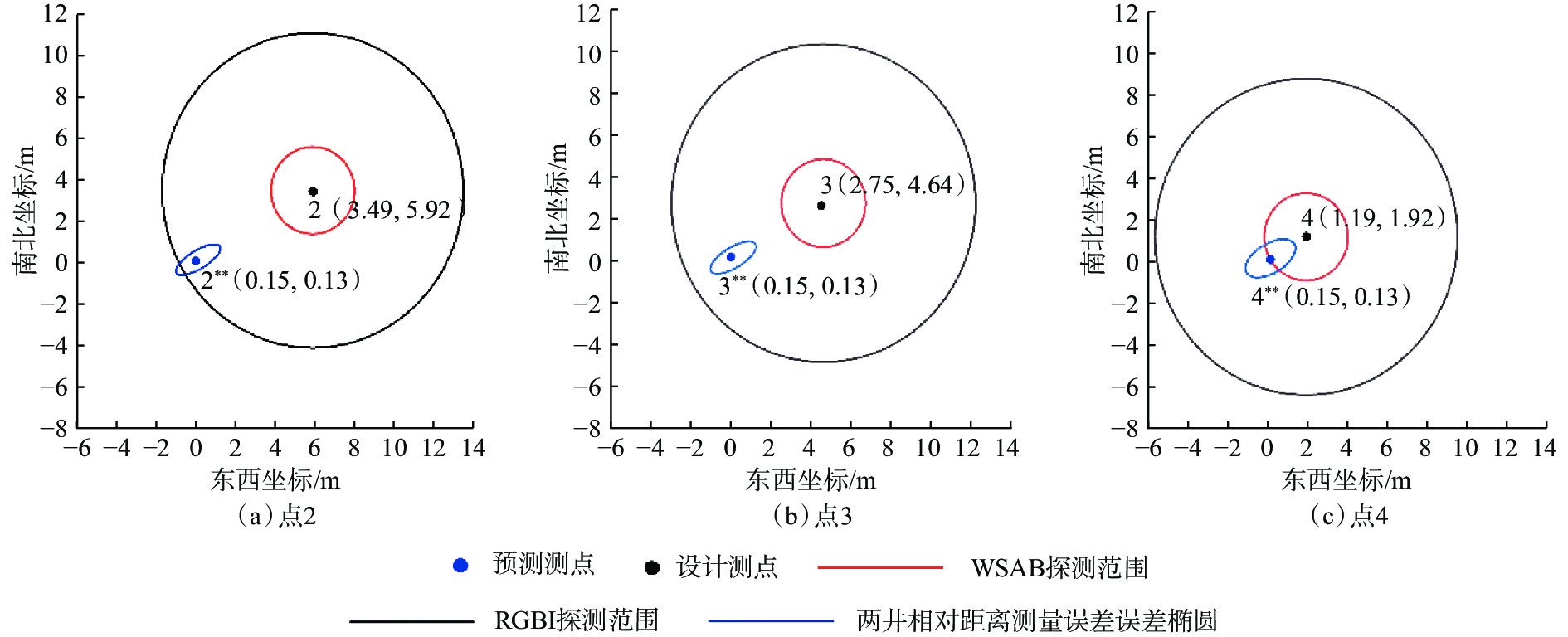
设计测点	N坐标/ m	E坐标/ m	预测相对距离/m	r₁	r₂	旋转角θ/ （°）
2	3.49	5.92	6.68	0.45	1.27	29.99
3	2.75	4.64	5.21	0.50	1.29	29.89
4	1.19	1.92	2.07	0.71	1.39	29.32

下载: 导出CSV

| 显示表格

根据表1、表2中的数据，分别绘制3个测点的两井相对距离测量误差椭圆及主动磁测距工具探测范围（见图6）。根据主动磁测距工具优选方法，若在点2处进行测距作业，为确保工具入井后可以探测到事故井套管，只能采用Wellspot工具；若在点3或点4处进行测距作业，此时两井相对位置误差椭圆在RGRⅠ与Wellspot工具探测范围内、但在WSAB工具探测范围外，因此可换用测量精度更高的RGRⅠ工具。

图 6 主动磁测距工具优选结果

Figure 6. Optimal selection result of active magnetic ranging tools

下载: 全尺寸图片幻灯片

5. 结　论

1）建立了可定量描述主动磁测距工具测量误差的计算模型，实现了事故井预测测点与救援井当前井底间的相对距离测量误差计算。

2）通过对比主动磁测距工具探测范围与两井相对距离测量误差椭圆的空间关系，给出了主动磁测距工具的优选方法，该方法可以在确保事故井可探测的前提下选用测量精度更高、作业风险更小的磁测距工具。

3）建立主动磁测距工具测量误差模型时，忽略了相对距离与相对方位之间的相关关系，后续应依据主动磁测距工具测量原理对误差源进行细化，以期实现对主动磁测距工具测量误差的精确描述。

图 1 磁测距工具引导两井连通过程示意

Figure 1. Connection process of two wells via magnetic ranging tools

下载: 全尺寸图片幻灯片

图 2 两井相对距离测量误差

Figure 2. Measurement error of the relative distance between the two wells

下载: 全尺寸图片幻灯片

图 3 磁测距作业时建立的坐标系示意

Figure 3. Diagram of the established coordinate systems

下载: 全尺寸图片幻灯片

图 4 主动电磁测距工具优选方法

Figure 4. Optimal selection method of active electromagnetic ranging tools

下载: 全尺寸图片幻灯片

图 5 主动磁测距工具测量误差示意

Figure 5. Measurement error of active magnetic ranging tools

下载: 全尺寸图片幻灯片

图 6 主动磁测距工具优选结果

Figure 6. Optimal selection result of active magnetic ranging tools

下载: 全尺寸图片幻灯片

表 1 主动电磁测距工具性能指标

Table 1 Performance indexes of active electromagnetic ranging tools

测距工具	探测范围/m	距离精度，%	方位精度/（°）	外径/mm	温度/℃	压力/MPa	备注
Wellspot	61.0	±20	±3	50.8	204.4	172.4	每次测距需要起下钻
WSAB	4.6	±20	±3	215.9	125.0	103.4	不需要起下钻
WSAB	2.1	±5	±3	50.8	125.0	103.4	不需要起下钻
RGRⅠ	7.6	±5	±3	114.3	176.6	137.9

下载: 导出CSV

表 2 预测测点处两井相对距离测量误差椭圆

Table 2 Predicted measurement error ellipses of the relative distances between the two wells at the ranging points

设计测点	设计测点坐标		预测相对距离/m	误差椭圆半径/m		旋转角θ/ （°）
设计测点	N坐标/ m	E坐标/ m	预测相对距离/m	r₁	r₂	旋转角θ/ （°）
2	3.49	5.92	6.68	0.45	1.27	29.99
3	2.75	4.64	5.21	0.50	1.29	29.89
4	1.19	1.92	2.07	0.71	1.39	29.32

下载: 导出CSV

参考文献(25)

[1]	刘书杰,李相方,何英明,等. 海洋深水救援井钻井关键技术[J]. 石油钻采工艺,2015,37(3):15–18. LIU Shujie, LI Xiangfang, HE Yingming, et al. Key drilling technology for marine deepwater relief wells[J]. Oil Drilling & Production Technology, 2015, 37(3): 15–18.
[2]	姜海涛. 救援井与事故井连通技术研究[D]. 北京: 中国石油大学（北京）, 2014. JIANG Haitao. Study on the technology of intercommunicating the relief well and the accident well[D].Beijing: China University of Petroleum(Beijing), 2014.
[3]	李翠,高德利,刘庆龙,等. 邻井随钻电磁测距防碰计算方法研究[J]. 石油钻探技术,2016,44(5):52–59. LI Cui, GAO Deli, LIU Qinglong, et al. A method of calculating of avoiding collisions with adjacent wells using electromagnetic ranging surveying while drilling tools[J]. Petroleum Drilling Techniques, 2016, 44(5): 52–59.
[4]	李翠,高丽萍,李佳,等. 邻井随钻电磁测距防碰工具模拟试验研究[J]. 石油钻探技术,2017,45(6):110–115. LI Cui, GAO Liping, LI Jia, et al. Experiment research on an electromagnetic anti-collision detection tool while drilling adjacent wells[J]. Petroleum Drilling Techniques, 2017, 45(6): 110–115.
[5]	ZHANG Sen, DIAO Binbin, GAO Deli. Numerical simulation and sensitivity analysis of accurate ranging of adjacent wells while drilling[J]. Journal of Petroleum Science and Engineering, 2020, 195: 107536. doi: 10.1016/j.petrol.2020.107536
[6]	李翠,高德利,刁斌斌,等. 基于三电极系救援井与事故井连通探测系统[J]. 石油学报,2013,34(6):1181–1188. doi: 10.7623/syxb201306020 LI Cui, GAO Deli, DIAO Binbin, et al. A detection system based on three-electrode array for connecting a relief well to failure well[J]. Acta Petrolei Sinica, 2013, 34(6): 1181–1188. doi: 10.7623/syxb201306020
[7]	许林康. 瞬变电磁法救援井近距离相对姿态识别方法研究[D]. 西安: 西安石油大学, 2020. XU Linkang. Research on the method of relative attitude recognition in near distance of relief well by TEM[D]. Xian: Xi'an Shiyou University, 2020.
[8]	付友义,周洪林,陈佳杰. 大港油田长新5磨铣套管救援井设计与实践[J]. 钻采工艺,2020,43(5):5–8. doi: 10.3969/J.ISSN.1006-768X.2020.05.02 FU Youyi, ZHOU Honglin, CHEN Jiajie. Design and application of Changxin 5 milled casing relief well in Dagang Oilfield[J]. Drilling & Production Technology, 2020, 43(5): 5–8. doi: 10.3969/J.ISSN.1006-768X.2020.05.02
[9]	郝希宁,王宇,党博,等. 救援井电磁探测定位方法及工具研究[J]. 石油钻探技术,2021,49(3):75–80. doi: 10.11911/syztjs.2021005 HAO Xining, WANG Yu, DANG Bo, et al. Research on electromagnetic detection and positioning methods and tools for relief wells[J]. Petroleum Drilling Techniques, 2021, 49(3): 75–80. doi: 10.11911/syztjs.2021005
[10]	张地平. 地下电磁定位测距方法研究[D]. 成都: 电子科技大学, 2018. ZHANG Diping. Research on location method of underground electromagnetic positioning[D]. Chengdu: University of Electronic Science and Technology of China, 2018.
[11]	李峰飞,蒋世全,周建良,等. 深水救援井井眼轨道设计探讨[J]. 石油钻探技术,2017,45(1):21–26. LI Fengfei, JIANG Shiquan, ZHOU Jianliang, et al. Discussion on the design of well trajectories in deepwater relief wells[J]. Petroleum Drilling Techniques, 2017, 45(1): 21–26.
[12]	李峰飞,蒋世全,李汉兴,等. 救援井电磁探测工具分析及应用研究[J]. 石油机械,2014,42(1):56–61. doi: 10.3969/j.issn.1001-4578.2014.01.014 LI Fengfei, JIANG Shiquan, LI Hanxing, et al. Analysis of electromagnetic probe for relief well[J]. China Petroleum Machinery, 2014, 42(1): 56–61. doi: 10.3969/j.issn.1001-4578.2014.01.014
[13]	龚大洪,陈元鹏,杨文娟,等. 一种井眼轨迹不确定性方法的可视化研究与应用[J]. 钻采工艺,2019,42(6):9–12. doi: 10.3969/J.ISSN.1006-768X.2019.06.03 GONG Dahong, CHEN Yuanpeng, YANG Wenjuan, et al. 3-D visual study of well trajectory uncertainty and application[J]. Drilling & Production Technology, 2019, 42(6): 9–12. doi: 10.3969/J.ISSN.1006-768X.2019.06.03
[14]	WILLIAMSON H S. Accuracy prediction for directional measurement while drilling[J]. SPE Drilling & Completion, 2000, 15(4): 221–233.
[15]	范光第, 蒲文学, 赵国山, 等. 磁力随钻测斜仪轴向磁干扰校正方法[J]. 石油钻探技术, 2017, 45(4): 121-126. FAN Guangdi, PU Wenxue, ZHAO Guoshan, et al. Correction methods for axial magnetic interference of the magnetic inclinometer while drilling[J]. Petroleum Drilling Techniques, 2017, 45(4): 121-126.
[16]	许昊东, 黄根炉, 张然, 等. 磁力随钻测量磁干扰校正方法研究[J]. 石油钻探技术, 2014, 42(2): 102-106. XU Haodong, HUANG Genlu, ZHANG Ran, et al. Method of magnetic interference correction in survey with magnetic MWD[J]. Petroleum Drilling Techniques, 2014, 42(2): 102-106.
[17]	李峰飞,蒋世全,周建良,等. 救援井探测定位方案设计研究[J]. 中国海上油气,2017,29(4):118–122. LI Fengfei, JIANG Shiquan, ZHOU Jianliang, et al. Research on the design of ranging plan for relief wells[J]. China Offshore Oil and Gas, 2017, 29(4): 118–122.
[18]	高德利,刁斌斌. 复杂结构井磁导向钻井技术进展[J]. 石油钻探技术,2016,44(5):1–9. GAO Deli, DIAO Binbin. Development of the magnetic guidance drilling technique in complex well engineering[J]. Petroleum Drilling Techniques, 2016, 44(5): 1–9.
[19]	ISCWSA. Introduction to wellbore positioning[R]. [S. l.]: The Research Office of UHI, 2017.
[20]	席宝滨,高德利. U形水平井连通过程中的相对位置不确定性分析[J]. 石油钻探技术,2014,42(6):18–24. XI Baobin, GAO Deli. Analysis of the relative position uncertainty in the intersecting process of U-shaped horizontal wells[J]. Petroleum Drilling Techniques, 2014, 42(6): 18–24.
[21]	李翠,高德利. 救援井与事故井连通探测方法初步研究[J]. 石油钻探技术,2013,41(3):56–61. doi: 10.3969/j.issn.1001-0890.2013.03.011 LI Cui, GAO Deli. Preliminary research on detection method for connecting relief well to blowout well[J]. Petroleum Drilling Techniques, 2013, 41(3): 56–61. doi: 10.3969/j.issn.1001-0890.2013.03.011
[22]	李翠. 救援井与事故井连通探测方法研究[D]. 北京: 中国石油大学（北京）, 2014. LI Cui. Research on detection method for making relief well connected to blowout well[D]. Beijing: China University of Petroleum(Beijing), 2014
[23]	胡圣武, 肖本林. 误差理论与测量平差基础[M]. 北京: 北京大学出版社, 2012: 48-52. HU Shengwu, XIAO Benlin. Error theory and measurement adjustment basis[M]. Beijing: Peking University Press, 2012: 48-52.
[24]	柳贡慧,董本京,高德利. 误差椭球及井眼交碰概率分析[J]. 钻采工艺,2000,23(3):5–12. doi: 10.3969/j.issn.1006-768X.2000.03.002 LIU Gonghui, DONG Benjing, GAO Deli. Probability analysis of error ellipsoid(ellipse) and hole intersection[J]. Drilling & Production Technology, 2000, 23(3): 5–12. doi: 10.3969/j.issn.1006-768X.2000.03.002
[25]	董本京,高德利,柳贡慧. 井眼轨迹不确定性分析方法的探讨[J]. 天然气工业,1999,19(4):59–63. DONG Benjing, GAO Deli, LIU Gonghui. Discussion on the analytical method of well track uncertainty[J]. Natural Gas Industry, 1999, 19(4): 59–63.

施引文献(10)

期刊类型引用(8)

1.	张淑霞，沐宝泉，严文娟，文萍. 稠油侵入钻井液技术研究进展. 当代化工. 2023(02): 411-414 . 百度学术
2.	葛祥，周贤杰，张世懋. 中东Y油田碳酸盐岩油藏沥青层测井评价. 测井技术. 2018(02): 149-155 . 百度学术
3.	江朝. 伊朗雅达油田F13井严重沥青侵复杂情况的处理. 复杂油气藏. 2017(02): 82-86 . 百度学术
4.	路保平，侯绪田，邢树宾. 伊朗雅达油田沥青层置换机制与压力波动分析. 中国石油大学学报(自然科学版). 2017(06): 88-93 . 百度学术
5.	江朝. ZDM型倒扣捞矛落井原因分析及改进应用. 石油机械. 2017(06): 99-102 . 百度学术
6.	江朝，张华卫，黄在福，侯立中，吴旭辉. 雅达油田F13井沥青层喷漏同存复杂情况的处理. 石油钻采工艺. 2017(04): 528-532 . 百度学术
7.	江朝，王利华，黄在福，侯立中，庞小旺. 雅达油田沥青层钻井风险预测方法探讨. 钻采工艺. 2017(04): 10-12+1 . 百度学术
8.	唐文泉，王成彪，金军斌，杨帆，薛玉志，陈晓飞，李涛，宋兆辉. 钻井工程中沥青与钻井液动态置换规律实验研究. 科学技术与工程. 2016(27): 20-25 . 百度学术

其他类型引用(2)

资源附件(0)

图(6) / 表(2)

计量

文章访问数: 660
HTML全文浏览量: 284
PDF下载量: 65
被引次数: 10

1. 相对距离测量误差组成分析
2. 相对距离测量误差计算
2.1 坐标系的建立及相对位置计算
2.2 主动磁测距工具测量误差计算
2.3 误差椭圆
3. 主动磁测距工具优选方法
3.1 主动磁测距工具分析
3.2 主动磁测距工具的优选方法
4. 算例分析
4.1 基础数据
4.2 计算与分析
5. 结　论

1. 相对距离测量误差组成分析
2. 相对距离测量误差计算
2.1 坐标系的建立及相对位置计算
2.2 主动磁测距工具测量误差计算
2.3 误差椭圆
3. 主动磁测距工具优选方法
3.1 主动磁测距工具分析
3.2 主动磁测距工具的优选方法
4. 算例分析
4.1 基础数据
4.2 计算与分析
5. 结　论

参考文献(25)

施引文献(10)

资源附件(0)

基于邻井距离测量误差的救援井磁测距工具优选方法

计量

出版历程