废弃高性能水基钻井液循环利用电吸附处理方法

任雯; 刘晓辉; 李盛林; 王飞; 仝坤; 张明栋

doi:10.11911/syztjs.2020046

废弃高性能水基钻井液循环利用电吸附处理方法

任雯^{1, 2,},
刘晓辉^{1, 2},
李盛林³,
王飞^{1, 2},
仝坤^{1, 2},
张明栋^{1, 2}

1.
石油石化污染物控制与处理国家重点实验室，北京 102206
2.
中国石油集团安全环保技术研究院有限公司，北京 102206
3.
中国石油集团川庆钻探工程有限公司安全环保质量监督检测研究院，四川德阳 618300

基金项目: 国家科技重大专项“页岩气和煤层气开发环境保护技术集成及关键装备”（编号：2016ZX05040-006）和中国石油重大科技专项“水基钻井废弃物循环利用及资源化技术研究与示范应用”（编号：2016E-1203）部分研究内容

详细信息

作者简介:
任雯（1985—），女，四川广元人，2006年毕业于西南石油大学生物工程专业，2009年获西南石油大学化学工程专业硕士学位，高级工程师，主要从事石油石化固体废物处理与资源化利用技术研究。E-mail：renwen@cnpc.com.cn

中图分类号: TE254⁺.2
计量
- 文章访问数: 1214
- HTML全文浏览量: 407
- PDF下载量: 55
出版历程
- 收稿日期: 2019-08-14
- 修回日期: 2020-04-14
- 网络出版日期: 2020-04-28
- 刊出日期: 2020-06-30

Electro-Sorption Treatment Method for Waste High Performance Water-Based Drilling Fluid

REN Wen^{1, 2,},
LIU Xiaohui^{1, 2},
LI Shenglin³,
WANG Fei^{1, 2},
TONG Kun^{1, 2},
ZHANG Mingdong^{1, 2}

1.
State Key Laboratory of Petroleum Pollution Control, Beijing, 102206, China
2.
CNPC Research Institute of Safety and Environmental Technology, Beijing, 102206, China
3.
Research Institute of Safety and Environmental Quality Supervision and Inspection, CNPC Chuanqing Drilling Engineering Company Limited, Deyang, Sichuan, 618300, China

摘要

摘要:
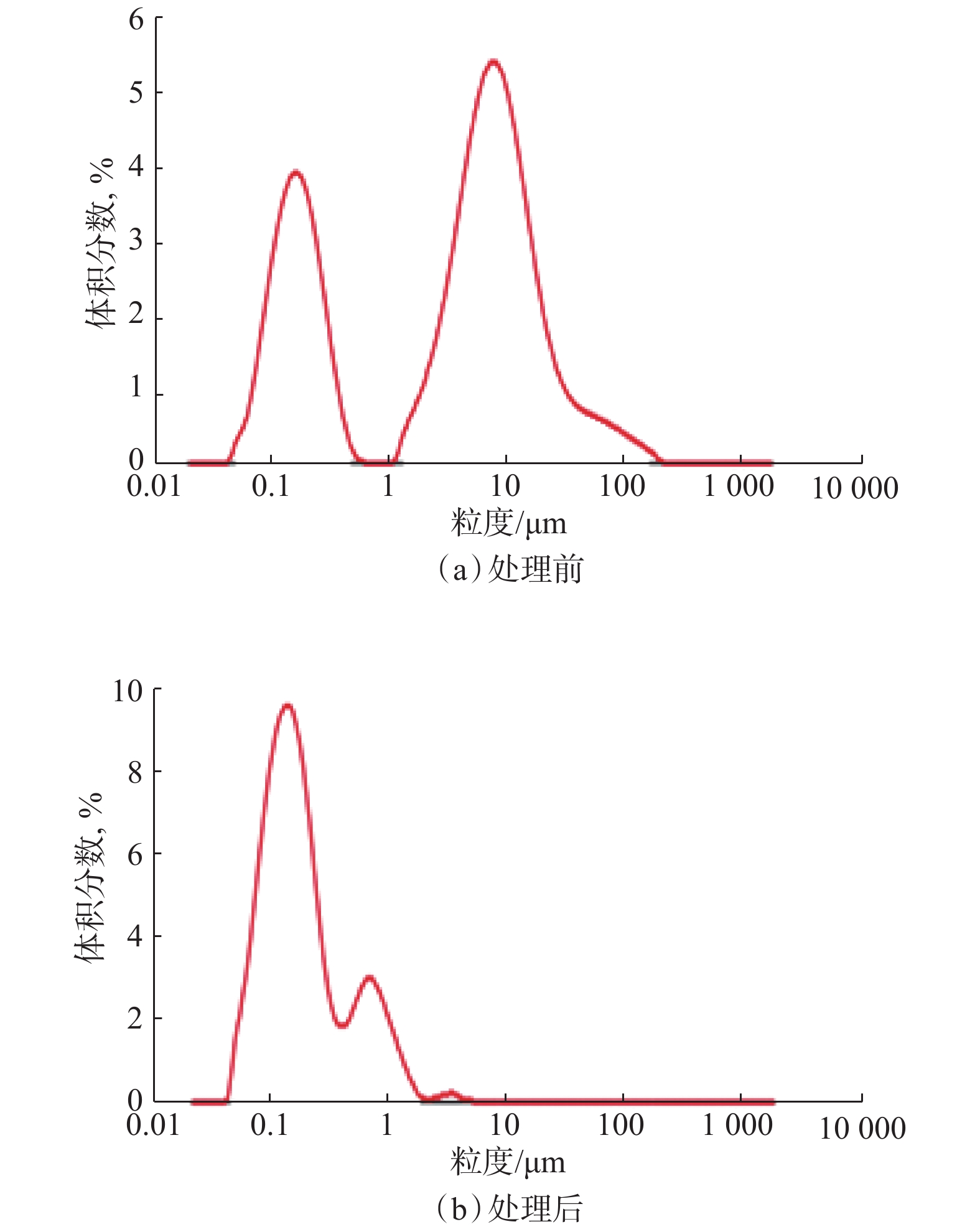
随着页岩气勘探开发环保要求的提高，钻井过程中逐步推广应用高性能水基钻井液，但仍产生大量的废弃钻井液。为了提高水基钻井液的循环利用率，分析了废弃高性能水基钻井液的总固相含量和微小劣质固相含量，提出了去除废弃高性能水基钻井液中劣质固相的电吸附处理方法，具有不添加化学药剂、选择性去除微小劣质固相和不破坏钻井液中原有有效成分等优点。试验结果表明，废弃高性能水基钻井液经过2次电吸附工艺处理后，能够去除粒径小于10 μm的超细微劣质固相；电吸附结合离心分离预处理方法能够显著提升高性能水基钻井液的再生性能，实现钻井液循环利用。研究结果表明，利用电吸附法处理废弃高性能水基钻井液，是废弃钻井液减量化和资源化处理新模式，具有较好的推广应用前景。
- 页岩气 /
- 水基钻井液 /
- 废物处理 /
- 电吸附 /
- 再生 /
- 循环利用
Abstract:
With the higher and higher environmental protection requirements for shale gas exploration and development, high-performance water-based drilling fluids have been gradually popularized in the drilling process. However,waste drilling fluid is still produced in a large amount. In order to improve the recycling efficiency of water-based drilling fluid, features of waste high-performance water-based drilling fluid, such as high content of total solid phase and micro poor solid phase, were analyzed, during which it was proposed to remove the poor solid phase in waste high-performance drilling fluid by the electro-sorption method, which had the advantages of having no addition of chemical agents, a selective removal of micro pore solid phase and no damage to the original effective components of drilling fluid. The experimental results showed that after taking the electro-sorption treatment process for two times, the ultra-fine and inferior solid phases of less than 10 μm in the waste high-performance water-based drilling fluid could be removed. Further, with the combination of electro-sorption method and centrifugal separation pretreatment, the performance of regenerated drilling fluid could be significantly improved, thus realizing the recycling of drilling fluid. The results obtained showed that the electro-absorption treatment of waste high-performance water-based drilling fluid constituted a new resource-based model for drilling fluid consumption reduction and reuse, which showed good potential for popularization and application.
- shale gas /
- water-based drilling fluid /
- waste disposal /
- electro-sorption /
- regeneration /
- recycling

HTML全文

对于高陡构造、大倾角等易斜地层的防斜打快，依靠常规钻直井的井斜控制技术已不能满足要求^[1–3]，迫切需要适用于高转速、高可靠及耐高温强振条件的低成本垂钻工具^[4–5]。自德国大陆深钻计划项目（kontinentales tiefborh programm der bundesrepublik deutschland，KTB）主孔（井深9 101 m）成功应用自动垂直钻井系统（VDS）以来，相继出现了贝克休斯公司的VertiTrak，斯伦贝谢公司的Power V等垂直钻井系统^[6–7]。但这些垂直钻井系统的机电液系统在井下高温（高于150 ℃）、强振动等复杂条件下适应性差、可靠性低^[8–9]。因此，近年来经济、安全、可靠的纯机械式自动垂直钻井系统逐渐受到关注，尤其在低油价的经济形势下，成为防斜打快钻井施工的最佳选择。

静态推靠机械式垂钻工具通过偏重块与动静盘阀组的相互作用实现井下实时闭环式主动防斜、纠斜，其盘阀的设计决定其能否保证井下垂钻应用效果^[10–12]。动静盘阀组作为该类垂钻工具的重要核心部件之一，摩阻设计决定着其分流导流效果，动静盘阀间缝隙决定着其密封效果，设计是否合理也是影响静态推靠机械式垂钻工具整体可靠性的关键因素之一。目前，国外类似结构大都采用电机驱动方式实现动静阀组的可控关断，与偏重驱动方式存在机理上的不同。因此，笔者对动静阀盘组进行了摩阻力计算，对环阀间隙流动进行了有限元分析，基于井眼高低边快速关断响应规律设计了环形阀结构及流道，并进行了地面台架试验，以期研制出高温、强振条件下经济、安全、可靠的静态推靠机械式垂钻工具。

1. 静态推靠机械式垂钻工具研制思路

1.1 工具结构

拟研制的静态推靠垂钻工具为纯机械式结构^[13–15]，由重力偏重稳定平台、双层推靠机构、动力芯轴以及PDC复合轴承等部件组成（如图1所示），是三层独立旋转系统，能够在钻井过程中实现主动防斜纠斜，是井下闭环钻井工具^[16–18]。

图 1 静态推靠机械式垂钻工具主要部件

Figure 1. Schematic diagram of static pushing tool composition

下载: 全尺寸图片幻灯片

静态推靠机械式垂钻工具通过重力偏重稳定平台动态响应井斜变化，响应精度要达到1°。动力芯轴传递钻压扭矩，隔离钻头破岩产生的振动冲击。经过滤的小排量高压钻井液可以净化轴承，为推靠机构提供动力源。安装在近钻头的双层静态推靠机构，利用钻头水压差可实现准静态推靠井壁，推靠力要达到10 kN以上。静态推靠机械式垂钻工具的基本结构如图2所示。

图 2 静态推靠机械式垂钻工具基本结构

1.上主轴；2.上轴承组；3.工具外壳；4.过滤短节；5.芯轴；6.偏重单元；7.动静阀盘组；8.推靠机构；9.下轴承组；10.下主轴

Figure 2. Structural diagram of static pushing tool

下载: 全尺寸图片幻灯片

1.2 工作原理

静态推靠机械式垂钻工具主要用于解决直井段钻井时的防斜打直问题。实际钻进中，该工具下端直接连接钻头，上端连常规钻具和螺杆钻具，通过芯轴实现钻压、转速等钻井工程参数的调整。钻井液主体部分通过芯轴中间流道过流，如图3所示黄色箭头。套在芯轴上的导向外筒不受其影响，基本上处于静止或缓慢转动状态。钻头位置存在流体压差，利用小排量钻井液驱动推靠机构与井眼高边相互作用，对钻具实现有效的静态推靠。当井斜角超出设计范围时，位于导向外筒内的偏重单元受到重力作用旋转，带动下端的上环形阀转到工具低边位置，并保持在一定的动态稳定精度范围内；位于下环形阀上高边的流道口打开，小排量的钻井液流入导向外筒高边位置的高压流道（如图3所示红色箭头），流入相应的活塞腔并推动活塞沿径向滑动，驱动翼肋向外伸出静态推靠井壁给井眼高边位置施加静态推靠力，推动钻具向井眼低边方向偏转，从而实现钻进中的纠斜。

图 3 静态推靠机械式垂钻工具工作原理示意

Figure 3. Working principle description diagram of static pushing tool

下载: 全尺寸图片幻灯片

2. 环形动静盘阀结构及流道设计

2.1 动静盘阀间摩擦阻力计算

盘阀间的摩擦阻力矩由动静盘阀组之间存在的压力差及上下盘阀的相对转动产生，常规上盘阀结构如图4所示（ $\alpha$ 为腰孔开孔角度，（°）； $\theta$ 为腰孔两端圆弧张开角度，（°）；r₀为腰孔两端圆弧半径，mm；r₁，r₂分别为上盘阀腰型孔的内、外半径，mm；d为上盘阀的内径，mm；D为上盘阀的外径，mm）。

图 4 上盘阀结构示意

Figure 4. Schematic diagram of upper disc valve structure

下载: 全尺寸图片幻灯片

盘阀间的摩擦阻力矩T_p可分为3部分进行计算，即：

${T_p} = {T_{p1}} + {T_{p2}} + {T_{p3}}$

(1)

式中： ${T_{p1}}$ 为上盘阀半径r在[d/2， ${r_1}$ ]范围内的摩擦阻力矩，N·m； ${T_{p2}}$ 为上盘阀半径r在（ ${r_1}$ ， ${r_2}$ ）范围内的摩擦阻力矩，N·m； ${T_{p3}}$ 为上盘阀半径r在[ ${r_2}$ ，D/2]范围内的摩擦阻力矩，N·m。

当上盘阀半径r位于[d/2， ${r_1}$ ]时，有：

$T_{p1}=\int_{\frac{d}{2}}^{r_1}2\mu\mathrm{_v}pr^2\mathrm{d}r=\frac{2}{3}\mu_{\mathrm{v}}p\left(r_1^3-\frac{d^3}{8}\right)$

(2)

当上盘阀半径r位于（ ${r_1}$ ， ${r_2}$ ）时，有：

${T_{p2}} = \int_{{r_1}}^{{r_2}} {\left( {2p - \alpha - 2\theta } \right){r^2}{\mathrm{d}}r}$

(3)

当上盘阀半径r位于[ ${r_2}$ ，D/2]时，计算与r位于[d/2， ${r_1}$ ]时相同。则此部分摩擦力矩为：

$T_{p3}=\int_{r_2}^{\frac{D}{2}}2\mu_{\mathrm{v}}pr^2\mathrm{d}r=\frac{2}{3}\mu\mathrm{_v}p\left(\frac{D^3}{8}-r_2^3\right)$

(4)

则盘阀总的摩擦力矩为：

$\begin{split} & T_p=\frac{2}{3}\mu\mathrm{_v}p\left(r_1^3-\frac{d^3}{8}\right)+ \\ &\int_{r_1}^{r_2}\left\{2p-\alpha-2\arccos\left[\frac{r^2+r_1r_2}{r\left(r_1+r_2\right)}\right]\right\}r^2\mathrm{d}r+\frac{2}{3}\mu\mathrm{_v}p\left(\frac{D^3}{8}-r_2^3\right) \end{split}$

(5)

式中： $\mu_{\mathrm{v}}$ 为盘阀间的摩擦系数； $p$ 为动静阀盘间的静水压力，MPa。

通过式（5）的计算结果可知，T_p与 $\mu$ ， $p$ 和 ${r^3}$ 成正比。在实际设计过程中， $p$ 往往为固定值， $\mu_{\mathrm{v}}$ 一般取值较小，减小的区间比较小。因此，减小 $r$ 的值是最有效的方式。

从另外一个角度考虑，盘阀的摩阻与半径的平方成正比，而半径的平方为盘阀面积，因此需要考虑减小盘阀接触面积。将与盘阀相配合的阀座设计为如图5所示结构，阀座处采用凸台形式，凸台直径为 ${D_0}$ ，其所在中心处直径为 $D_{\mathrm{f}}$ ，数量为3个。

图 5 阀座结构

Figure 5. Valve seat structure diagram

下载: 全尺寸图片幻灯片

凸台处的摩阻计算公式为：

$F_{\mathrm{n}}=n\text{π}p_{\mathrm{b}}R^2$

(6)

式中： ${F_{\mathrm{n}}}$ 为凸台处正压力，N；n为凸台数，此处取3； $p_{\mathrm{b}}$ 为钻头压降，MPa；R为凸台半径，mm，此处取 ${D_0}/2$ 。

该处摩擦力为：

${F_{\mathrm{f}}} = {F_{\mathrm{n}}}{\mu _{\mathrm{v}}}$

(7)

式中： ${F_{\mathrm{f}}}$ 为凸台处的摩擦力，N。

则摩擦阻力矩：

${T_p} = {F_{\mathrm{f}}}\frac{{{D_{\mathrm{f}}}}}{2}$

(8)

为有效减小盘阀上下流体压力的作用面积，从而降低盘阀间摩擦阻力，盘阀采用如图5所示凸台接触式结构。凸台结构的存在使动静上下盘阀组间存在间隙，产生一定排量的泄流，而泄流量的大小直接关系到钻具各个推靠机构上侧向作用力的大小，进而对钻具的纠斜效果产生影响。因此，设计环阀间隙是否合理，是实现可控分流保压的技术关键，需要对盘阀缝隙流动开展有限元数值模拟分析，为盘阀的结构设计及优化提供依据。

2.2 环阀间隙的有限元计算分析

2.2.1 分析方法与湍流模型

采用计算流体动力学（computational fluid dynamics，CFD）方法研究盘阀间隙对钻具内部流场的影响，模拟分析了恒定泵量条件下钻具内部流场的压力变化。CFD采用有限体积法进行离散化，以物体运动三大守恒定律为基础，推导出复杂流场中流体运动的控制方程。

目前应用于计算流体力学的湍流模型，主要包括代数湍流模型和运输方程湍流模型两大类。代数湍流模型主要为增强黏度模型，其计算精度一般低于运输方程模型。运输方程模型采用剪切应力输运（shear stress transport，SST） $\kappa - \omega$ 模型，该模型通过混合函数在边界层内使用 $\kappa - \omega$ 模型，在边界层之外的湍流核心区使用 $\kappa - \varepsilon$ 模型，可以有效预测逆压梯度条件下流体分离的开始点和分离区大小，并快速获得收敛解^[19–20]。SST的 $\kappa - \omega$ 模型的湍动能运输方程及湍流比耗散方程分别为：

$\frac{\partial\rho\kappa}{\partial t}+\frac{\partial}{\partial x_j}\left[\rho v_j\kappa-\left(\mu+\sigma_{\kappa}\mu_t\right)\right]=\tau_{ij}S_{ij}-\beta^*\rho\omega\kappa$

(9)

$\begin{split} \frac{\partial\rho\omega}{\partial t}+ & \frac{\partial}{\partial x_j}\left[\rho v_j\omega-\left(\mu+\sigma_{\omega}\mu_t\right)\frac{\partial\omega}{\partial x_j}\right]= \\ &P_{\omega}-\beta_{\mathrm{c}}\rho\omega^2+2\left(1-F_1\right)\frac{\rho\sigma_{\omega}}{\omega}\frac{\partial\kappa\partial\omega}{\partial x_j\partial x_j} \end{split}$

(10)

${\mu _t} = \frac{{\rho \kappa}}{\omega }$

(11)

式中：ρ为流体密度，kg/m³；κ为湍动动能，J； ${x_j}$ 为空间坐标，m； $v_j$ 为速度分量，m/s； $\mu$ 为分子黏度，Pa·s；μ_t为t时刻的分子黏度，Pa·s； ${\sigma _\kappa}$ 为湍动能的普朗特常量； ${\tau _{ij}}$ 为湍流应力张量，Pa； ${S_{ij}}$ 为应变率张量，1/s； ${\beta ^*}$ 为湍流衰减系数；ω为湍流比耗散，1/s； ${\beta _c}$ 和 ${\sigma _\omega }$ 为经验常数； ${F_1}$ 为SST模型的混合函数； ${P_\omega }$ 为 $\omega$ 生成项，与平均速度梯度等有关。

${P_\omega }$ 的表达式为：

${P_\omega } = 2\gamma \rho \left( {{S_{ij}} - \frac{\omega {S_{nn}}{S_{ij}}}{3}} \right) - \frac{2\rho \kappa{S_{ij}}}{3}$

(12)

式中： $\gamma$ 为模型参数； $S_{n n}$ 为克罗内克算子。

雷诺应力的涡黏性模型为：

${\tau _{ij}} = 2{\mu _t}\left( {{S_{ij}} - \frac{{S_{nn}}{S_{ij}}}{3}} \right) - \frac{2\rho \kappa{S_{ij}}}{3}$

(13)

以水为不可压缩流体介质（ $\rho=1.0$ kg/m³），马赫数很低，雷诺数很高。基于上述分析，模拟分析用基本方程：

$\left\{ {\begin{array}{*{20}{l}} {\rho \left( {{\boldsymbol{v}} \cdot \nabla } \right){\boldsymbol{v}} = \nabla \cdot \left[ { - p{\boldsymbol{I}} + \left( {\mu + {\mu _t}} \right)\left( {\nabla {\boldsymbol{v}} + {{\left( {\nabla {\boldsymbol{v}}} \right)}^T}} \right)} \right] + {\boldsymbol{F}}} \\ {\rho \nabla \cdot {\boldsymbol{v}} = 0} \\ {\rho \left( {{\boldsymbol{v}} \cdot \nabla } \right)\kappa = \nabla \cdot \left[ {\left( {\mu + {\mu _t}{\sigma _\kappa}} \right)\nabla \kappa} \right] + \tau {i_j}{S_{ij}} - {\beta ^*}\rho \omega \kappa} \\ \rho \left( {{\boldsymbol{v}} \cdot \nabla } \right)\omega = \nabla \cdot \left[ {\left( {\mu + {\mu _t}{\sigma _\omega }} \right)\nabla \omega } \right] + \dfrac{\gamma }{{{\mu _t}}}\rho p - \rho {\beta _{\mathrm{c}}}{\omega ^2} +\\ 2\left( {1 - {F_1}} \right)\dfrac{{{\sigma _\omega }\rho }}{\omega }\nabla \kappa \cdot \nabla \omega \end{array}} \right.$

(14)

式中：v为速度场；I为单位矩阵；T为温度，K；F为外力场，包括重力、磁力等； $\nabla$ 表示梯度运算。

壁距离是CFD模拟中关键的几何量之一，指流体中某一点到物体边界或壁面的垂直距离，用于描述流体与固体表面之间的关系。壁距离 ${l_{\mathrm{w}}}$ 初始化方程为：

$\left\{ {\begin{array}{*{20}{l}} {\nabla G \cdot \nabla G + {\sigma _\mathrm{w}}G\left( {\nabla \cdot \nabla G} \right) = \left( {1 - 2{\sigma _\mathrm{w}}} \right){G^4}} \\ {{l_\mathrm{w}} = \dfrac{1}{G} - \dfrac{l_\mathrm{ref}}{2}} \end{array}} \right.$

(15)

式中：G为壁距离倒数，1/m； ${l_{{\mathrm{ref}}}}$ 为参考比例长度，m。

入口控制方程为：

$\left\{\begin{array}{*{20}{l}}\boldsymbol{v}=-\dfrac{M_{\mathrm{f}}}{\rho}\boldsymbol{n} \\ \nabla G\cdot\boldsymbol{n}=0 \\ M_{\mathrm{f}}=\dfrac{\rho V_{\mathrm{L}}}{\text{π}R^2t}\end{array}\right.$

(16)

式中：n为法向单位向量； ${M_{\mathrm{f}}}$ 为逐点质量流率，kg/(m²·s)； ${V_{\mathrm{L}}}$ 为入口处单位时间通过的流体体积，m³；R为入口处半径，mm；t为时间，s。

出口控制方程为：

$\left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{n}}^T}\left[ { - p{\boldsymbol{I}} + \left( {\mu + {\mu _T}} \right)\left( {\nabla {\boldsymbol{v}} + {{\left( {\nabla {\boldsymbol{v}}} \right)}^T}} \right)} \right]{\boldsymbol{n}} {\hat p{_0}} } \\ {{\hat p{_0}} < {p_0},{\boldsymbol{v}} \cdot t = 0} \\ {\nabla \kappa \cdot {\boldsymbol{n}} = 0,\nabla \omega \cdot {\boldsymbol{n}} = 0,\nabla G \cdot {\boldsymbol{n}} = 0} \end{array}} \right.$

(17)

式中： ${{\hat p_0}}$ ， ${p_0}$ 分别为出口预设压力和出口理论压力，MPa；μ_T为温度T时的分子黏度，Pa·s。

模拟过程中，设流体通道壁为无滑移边界条件，则控制方程为：

${\boldsymbol{v}} = 0;k = 0;\omega = \mathop {\lim }\limits_{{l_{\mathrm{w}}} \to 0} \frac{{6v}}{{{\beta _1}l _{\mathrm{w}}^2}},{l _{\mathrm{w}}} = 0$

(18)

CFD模拟用主要参数κ为0.41，β^*为9/100，β_c1为0.075，β_c2为0.0828，γ₁为5/9，γ₂为0.44，σ_κ1为0.85，σ_κ2为1，σ_ω1为0.5，σ_ω2为0.856。综合分析这些参数，基于ANSYS Workbench平台构建了三维瞬态流程模型：根据图6流道尺寸进行参数化建模，特征尺寸公差小于0.01 mm；采用边界层加密方法，近壁面第一层厚度为0.02 mm；选用SST的 $\kappa - \omega$ 湍流模型进行求解设置，并进行网格无关性分析，结果表明模型可靠。

图 6 工具内部流道示意

Figure 6. Schematic diagram of internal flow channel of the tool

下载: 全尺寸图片幻灯片

2.2.2 模拟分析结果

静态推靠机械式垂钻工具的工作原理，主要是在不影响其工作压力的前提下，分流部分流体通过工具，并在偏重平台的作用下利用上、下盘阀产生高低压配流，高压部分流体推动相应执行机构推出，从而产生纠斜效果，在这过程中，三部分流体压力有重要的作用：首先是系统压力，为了不影响钻具正常工作，需保证系统增加本垂钻工具后，在一定的系统流量(60 L/s)下，通过调节钻头水眼的尺寸保证钻具正常工作，即系统压力不会因增加本工具而无法调整至正常状态，系统压力一般要求在3～5 MPa；其次是盘阀处流体压力，由于盘阀处的流体压力作用于上下盘阀接触表面，由于盘阀间存在摩擦系数，该部分正压力产生阻碍盘阀间相对运动的阻力，因此该部分压力往往要求越小越好，该处压力越小，同样偏心块作用下偏重平台的灵敏度就越高，即要达到相同的灵敏度所需的偏重平台长度就越小；再次是推靠活塞处压力，该部分压力直接决定执行机构推靠力的大小，根据实际纠斜需求，要求工具达到10～20 kN推靠力，根据计算，推靠活塞处系统压力应在1～2 MPa。

由以上分析可知，进行工具内部流体模拟的目的有2个：1）确定怎样的流道设计可以满足工具的使用要求，即在60 L/s的流量作用下，系统压力可达到3～5 MPa，推靠活塞处的压力为1～2 MPa，同时盘阀处的流体压力尽可能小；2）通过模拟得到可保证工具正常工作的钻头水眼组合。

分析工具内部流道，得到其简化流道及模拟模型，如图6所示。模拟模型中作如下假设：

1）盘阀间无间隙。静态推靠机械式垂钻工具盘阀间为凸台式结构，上下盘阀间有0.5 mm间隙。由于该间隙太小，而工具实际尺寸较大，若在模拟过程中包含该缝隙，将导致模拟整体网格数量及计算量大幅增加，因此在模拟过程中将该间隙忽略，并针对该缝隙流进行了专门分析。

2）上下轴承缝隙泄流简化为一当量直径孔泄流。由于径向轴承在使用过程中，公轴承与母轴承之间往往需要有约0.3 mm的间隙，在轴承工作时会形成泄漏流动。泄流通道的几何形状对流体流动的影响主要由其直径决定，将复杂的缝隙流动简化为具有相同流动特性的当量直径孔流动，可以更方便地利用已有的理论和经验公式进行计算和分析。这种简化假设允许我们在不考虑缝隙的详细形状和复杂性情况下，仍能准确预测流体的运动状态。

模拟模型中各进出口及系统边界条件参数：入口直径为55.0 mm，上轴承泄流当量直径为10.0 mm，下轴承泄流当量直径为10.0 mm，推靠活塞泄流口直径为3.0 mm，入口流量为60 L/s。

根据伯努利方程，沿流线方向，流体的压强、流速的平方与高度的线性组合是一个常数C：

${p_{\mathrm{L}}} + \frac{1}{2}{\rho _{\mathrm{L}}}v_{\mathrm{L}}^2 + {\rho _{\mathrm{L}}}gh = C$

(19)

式中： ${p_{\mathrm{L}}}$ 为流场内部流体压力，MPa； ${\rho _{\mathrm{L}}}$ 为钻井液的密度，kg/m³； ${v_{\mathrm{L}}}$ 为钻井液的流速，m/s；h为液流位置距地面的距离，m。

在恒定泵量钻井过程中，当钻具内部流场发生横截面积变化时，因钻井液流速变化，横截面积变化前后钻具内部的钻井液压力变化量为 $\Delta {p_{\mathrm{L}}}$ （忽略液流位置距地面距离的变化及钻具内部沿程压降的影响）， $\Delta {p_{\mathrm{L}}}$ 可以表示为：

$\Delta {p_{\mathrm{L}}} = {p_{{\mathrm{L}}1}} - {p_{{\mathrm{L}}2}} = \frac{1}{2}{\rho _{\mathrm{L}}}{\left( {\frac{{{Q_{\mathrm{L}}}}}{{{S_{D2}}}}} \right)^2} - \frac{1}{2}{\rho _{\mathrm{L}}}{\left( {\frac{{{Q_{\mathrm{L}}}}}{{{S_{D1}}}}} \right)^2}$

(20)

式中：p_L1，p_L2为钻具内部流场横截面积变化前后的流场压力，MPa；Q_L为钻井液流量，m³/s；S_D1，S_D2为钻具内部流场横截面积变化前后的横截面积，m²。

钻具内部流场模拟用主要设计及工艺参数：入口直径为55.0 mm，喷嘴半径为5.0 mm，喷嘴为5个，流量为3 600 L/min，活塞间隙为0.1 mm，出口压力为0 MPa。模拟分析中，主要考虑钻具内部压力降，忽略钻具外部环空中钻井液的压力，因此设定出口压力为0 MPa。若不考虑活塞间隙处的出口，在无盘阀间隙时，可得钻具内部流场压力降约2.92 MPa。在设定活塞间隙为出口后，通过模拟计算出的盘阀最大压力为2.16 MPa，小于理论计算结果，与实际情况基本吻合，如图7所示。

图 7 盘阀间无缝隙时流场的速度和压力云图

Figure 7. Cloud map of velocity and pressure in the flow field without gaps between disc valves

下载: 全尺寸图片幻灯片

当盘阀的缝隙分别为0.2，0.5，1.0和5.0 mm时钻具内部流场的流速和压力如图8所示。

图 8 不同盘阀间隙下工具内部流场的速度和压力云图

Figure 8. Cloud map of velocity and pressure in the internal flow field of the tool when the gap between the disc valve is 0.2-0.5-1.5 mm

下载: 全尺寸图片幻灯片

从图8可以看出，随着盘阀间隙逐步增大，钻具内部流场的最大流速和最大压力均呈现逐渐减小的趋势，但钻具内部最大流速和最大压力的位置基本保持一致，最大流速出现在等效钻头喷嘴位置，最大压力位于盘阀上方。

盘阀间隙对盘阀附近流场影响的局部放大图见图9。从图9可以看出，当盘阀间隙＜0.5 mm时，低压钻井液流道的内部压力较小，且随着盘阀间隙增大，低压钻井液流道的内部压力缓慢增大，当盘阀间隙为1.0和2.0 mm时，低压钻井液流道的压力明显增大，且增幅较＜0.5 mm时明显加快。当盘阀间隙为5.0 mm时，盘阀右侧钻井液流道压力基本保持一致，表明此时不再存在低压钻井液流道，盘阀失去密封作用。

图 9 不同盘阀间隙下盘阀流场局部放大图

Figure 9. Localized enlarged view of flow field in disc valves with different clearances

下载: 全尺寸图片幻灯片

分析了钻具活塞两侧压差及盘阀下部井眼高边与低边钻井液通道压差变化随盘阀间隙的变化趋势，结果如图10所示。

图 10 盘阀间隙对流体压差的影响

Figure 10. Influence of disc valve clearance on fluid pressure difference

下载: 全尺寸图片幻灯片

由图10可知，为保证钻具正常工作，须严格控制盘阀的泄流量，应将盘阀间隙控制在0.5 mm以下，此时盘阀下井眼低边一侧钻井液通道内的压力与盘阀间无缝隙时的变化较小，在允许盘阀一定泄流量的前提下，起到一定的“密封”作用，保证钻具正常工作。通过以上分析，最终确定上下盘阀间隙为0.5 mm，上下盘阀凸台高度均为0.25 mm。

3. 地面台架试验

在全尺寸试验台架开展了ϕ177.8 mm静态推靠机械式垂钻工具的地面水力台架试验，用以验证该工具的主要功能。具体为：1）验证该工具在模拟现场机泵排量及压差下的整机性能；2）验证该工具在−4°～4°井斜角变化范围内推靠翼肋的启动角度，确定重力测斜稳定平台机构的响应精度；3）验证该工具在不同压差下的翼肋推靠力值范围及互锁功能；4）验证不同排量下该工具两端轴承处、推靠翼肋处的泄流情况。

根据试验数据得到了推靠力随压差变化的曲线、工具内部无效压耗随排量的变化曲线，分别如图11、图12所示。

图 11 推靠力随压差的变化曲线

Figure 11. The pushing force changes with the pressure difference

下载: 全尺寸图片幻灯片

图 12 工具内部无效压耗随排量的变化曲线

Figure 12. The variation curve of the ineffective pressure loss inside the tool with the displacement

下载: 全尺寸图片幻灯片

由图11、图12可知，翼肋启动大约需0.3 MPa，推靠力随着压差增大基本为线性增加，有效压耗占比（推靠力）最大为94.46%，平均在80%左右。静态推靠机械式垂钻工具两端PDC轴承的泄漏，使得该工具内部存在无效压力损耗，在试验压差范围内无效压耗平均为0.27 MPa。通过调整推靠翼肋的方位，观察翼肋出水孔的出水情况，90°方位位置只有1个推板翼肋出水，表明稳定平台的上下环阀密封正常，只有高边导流孔导通，其他孔没有导通。转动外筒至45°方位，两个推板翼肋同时推出，两个推板的出水孔均衡出水，表明稳定平台导向正常，密封良好。转动外筒至75°方位，两个高边翼肋同时推出，出水不均衡，靠近高边位置的出水强度大，远离高边位置的出水强度小，表明稳定平台控制动静阀盘组导向分流正常，密封保压性能指标达到了预期的设计要求。

4. 结论与建议

1）为研制高温、强振条件下经济、安全、可靠的静态推靠机械式垂钻工具，对其关键部件导流盘阀进行了研究与设计。根据盘阀摩阻力计算结果，为减小盘阀上下流体压力的作用面积，从而减小盘阀间摩擦阻力的作用，将动静阀盘组之间设计为凸台接触式结构。

2）针对上下盘阀之间的缝隙流动进行了有限元数值模拟，确定上下盘阀间隙应控制在0.5 mm，上下盘阀凸台高度均控制在0.25 mm。

3）在全尺寸试验台架开展了ϕ177.8 mm静态推靠机械式垂钻工具的地面水力台架试验，验证了所设计盘阀的密封性、导流性。

4）静态推靠机械式垂钻工具采用纯机械部件，集合了国内外垂钻工具的技术优势，能够克服高温、高转速及振动冲击等制约条件。建议加快现场试验及推广应用，优化迭代，为高陡构造等易斜地区提供低成本的防斜打快新技术。

图 1 废弃高性能水基钻井液电吸附处理中试装置

Figure 1. The electro-sorption pilot device of waste high-performance water-based drilling fluids

下载: 全尺寸图片幻灯片

图 2 不同电极板间距对吸附固相颗粒质量的影响

Figure 2. The effect of different plate spacing on the quality ofadsorbed solids

下载: 全尺寸图片幻灯片

图 3 不同吸附反应时间对吸附固相颗粒质量的影响

Figure 3. The Effect of different adsorption time on the qualityof adsorbed solids

下载: 全尺寸图片幻灯片

图 4 不同吸附电压对吸附固相颗粒质量的影响

Figure 4. The effect of different voltages on the quality ofadsorbed solid

下载: 全尺寸图片幻灯片

图 5 废弃高性能水基钻井液样品固相颗粒粒度分布

Figure 5. Size distribution of solid particles before adsorption of waste high performance water-based drilling fluid

下载: 全尺寸图片幻灯片

图 6 废弃高性能水基钻井液一次吸附后的固相颗粒粒度分布

Figure 6. Solid particle size distribution of waste high-performance water-based drilling fluid after primary adsorption

下载: 全尺寸图片幻灯片

图 7 废弃高性能水基钻井液二次吸附后的固相颗粒粒度分布

Figure 7. Solid particle size distribution of waste high-performance water-based drilling fluid after secondary adsorption

下载: 全尺寸图片幻灯片

图 8 废弃高性能水基钻井液离心分离处理前后的固相颗粒粒度分布

Figure 8. Particle size distribution of solid particles before and after centrifugation of waste high-performance water-based drilling fluid

下载: 全尺寸图片幻灯片

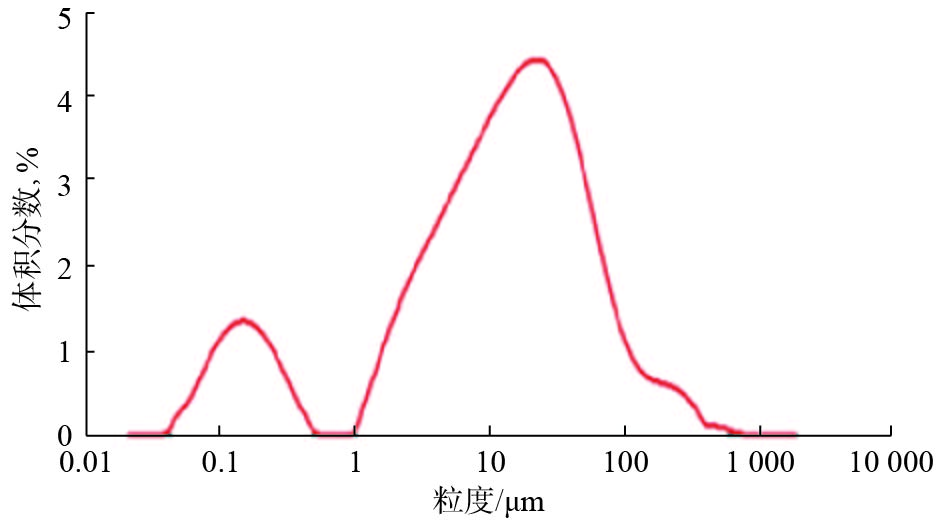
表 1 废弃高性能钻井液2次电吸附前后的性能

Table 1 Performance of waste high-performance drilling fluid before and after two electro-sorption treatment process

条件	密度/（kg·L⁻¹）	表观黏度/（mPa·s）	塑性黏度/（mPa·s）	动切力/Pa	静切力/Pa		六速旋转黏度计读数
条件	密度/（kg·L⁻¹）	表观黏度/（mPa·s）	塑性黏度/（mPa·s）	动切力/Pa	初切	终切	ϕ600	ϕ300	ϕ6	ϕ3
吸附前	1.78	104.0	84	24.0	2.5	5.0	293	169	10	7
一次吸附	1.68	101.5	80	17.5	2.5	5.5	208	128	10	7
二次吸附	1.55	85.5	72	13.5	1.6	6.0	171	99	6	4

下载: 导出CSV

表 2 废弃高性能钻井液离心及电吸附处理前后的性能

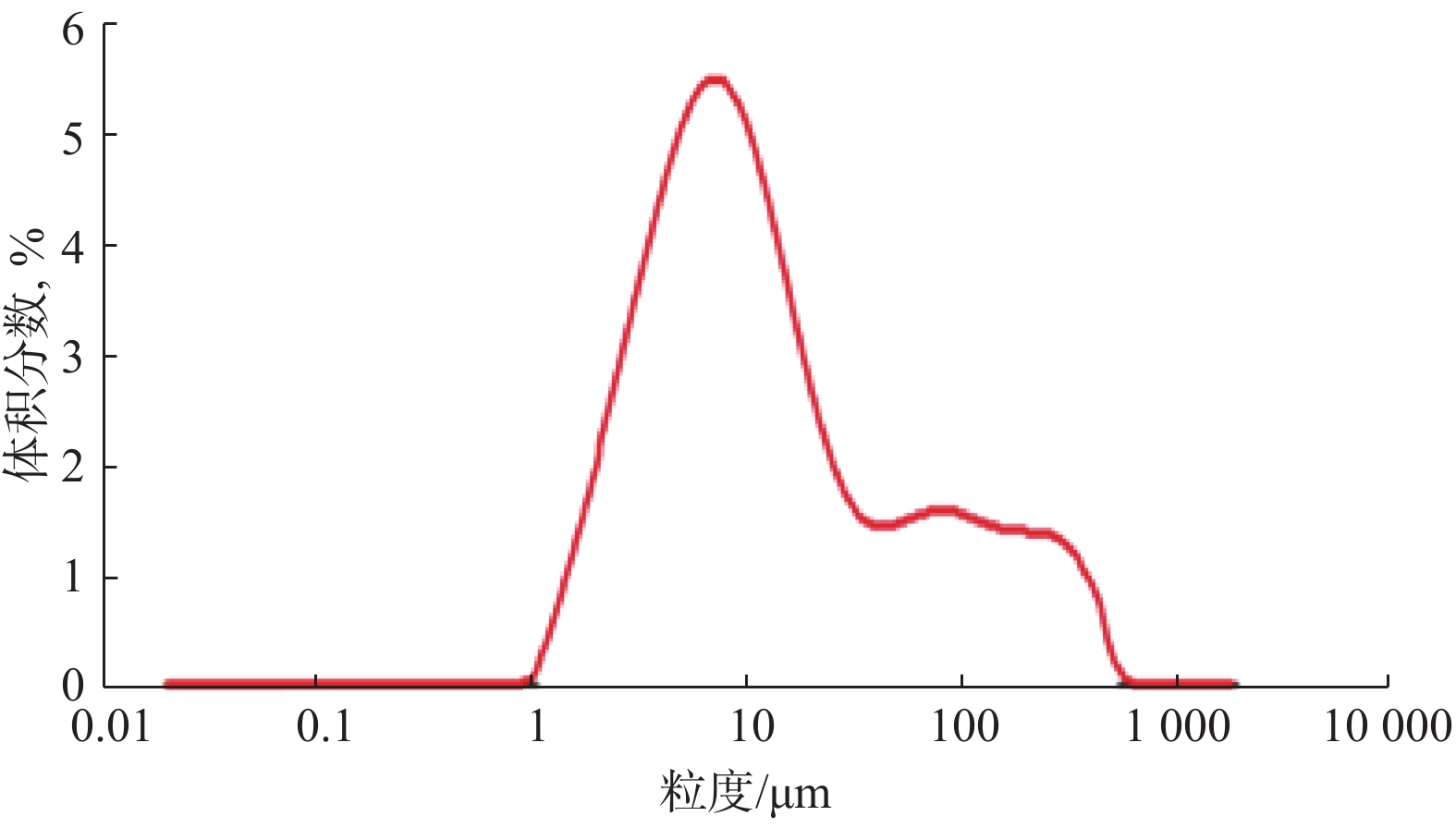
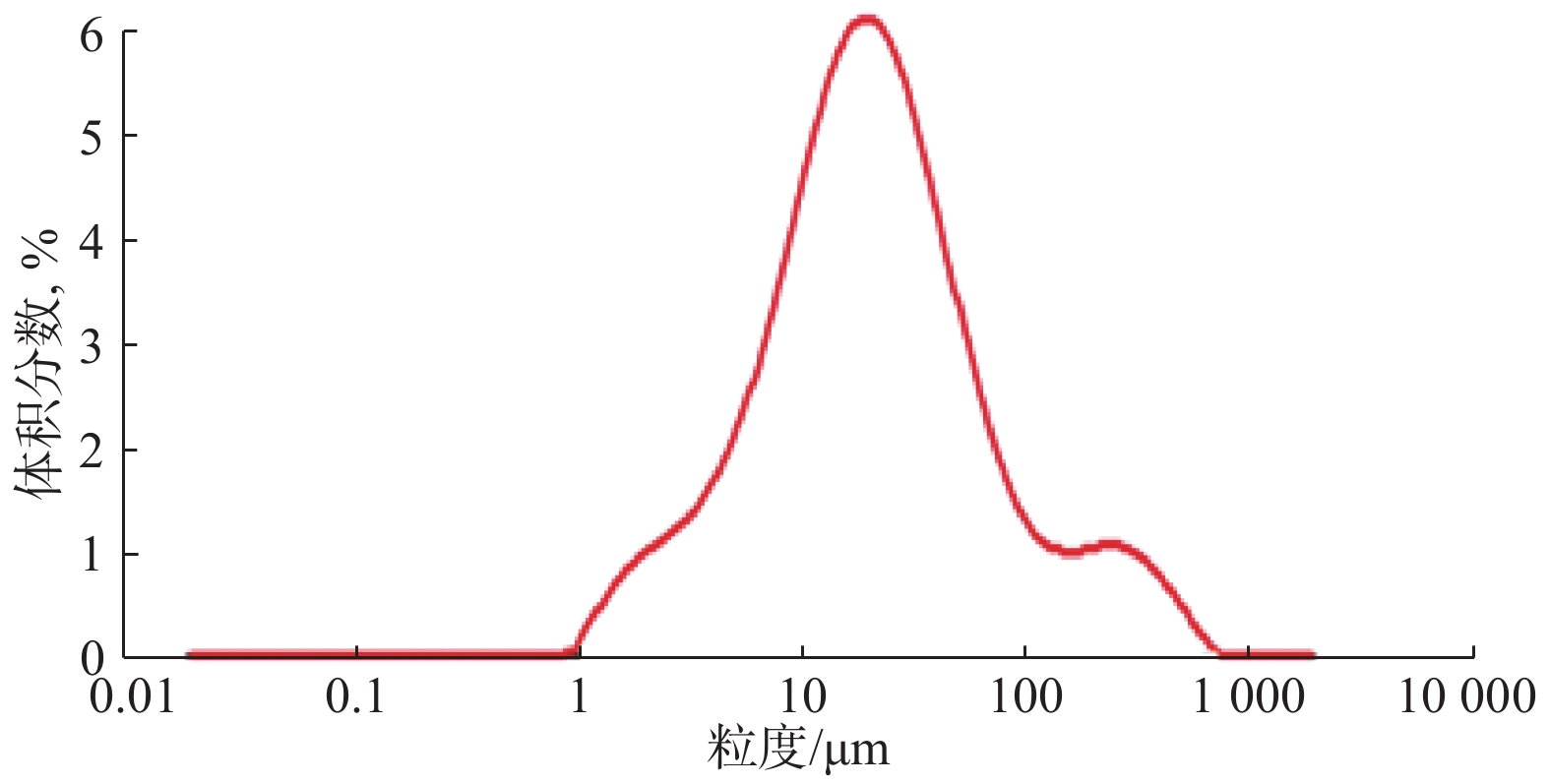
Table 2 Performance of waste high-performance drilling fluid before and after centrifugation and electro-sorption

指标项	密度/（kg·L⁻¹）	表观黏度/（mPa·s）	塑性黏度/（mPa·s）	动切力/Pa	静切力/Pa		六速旋转黏度计读数
指标项	密度/（kg·L⁻¹）	表观黏度/（mPa·s）	塑性黏度/（mPa·s）	动切力/Pa	初切力	终切力	ϕ600	ϕ300	ϕ6	ϕ3
处理前	1.65	93.0	76	17.0	5.0	8.0	186	110	6	3
离心后	1.39	50.5	25	4.5	3.0	6.0	61	35	2	1
电吸附后	1.17	28.0	16	3.0	2.5	5.0	56	31	2	1

下载: 导出CSV

参考文献(17)

[1]	刘尧文. 涪陵页岩气田绿色开发关键技术[J]. 石油钻探技术, 2018, 46(5): 8–13. LIU Yaowen. Key technologies of green development in the Fuling Shale Gas Field[J]. Petroleum Drilling Techniques, 2018, 46(5): 8–13.
[2]	刘永贵. 大庆致密油藏水平井高性能水基钻井液优化与应用[J]. 石油钻探技术, 2018, 46(5): 35–39. LIU Yonggui. Optimization and application of high performance water-based drilling fluid for horizontal wells in Daqing tight oil reservoir[J]. Petroleum Drilling Techniques, 2018, 46(5): 35–39.
[3]	徐加放,邱正松,吕开河. 泥页岩水化–力学耦合模拟实验装置与压力传递实验新技术[J]. 石油学报, 2005, 26(6): 115–118. doi: 10.3321/j.issn:0253-2697.2005.06.027 XU Jiafang, QIU Zhengsong, LYU Kaihe. Pressure transmission testing technology and simulation equipment for hydra-mechanics coupling of shale[J]. Acta Petrolei Sinica, 2005, 26(6): 115–118. doi: 10.3321/j.issn:0253-2697.2005.06.027
[4]	邸伟娜,闫娜,叶海超. 国外页岩气钻井液技术新进展[J]. 钻井液与完井液, 2014, 31(6): 76–81. doi: 10.3969/j.issn.1001-5620.2014.06.021 DI Weina, YAN Na, YE Haichao. Overseas new progresses in nano drilling fluid technology for shale drilling[J]. Drilling Fluid & Completion Fluid, 2014, 31(6): 76–81. doi: 10.3969/j.issn.1001-5620.2014.06.021
[5]	何振奎. 页岩水平井斜井段强抑制强封堵水基钻井液技术[J]. 钻井液与完井液, 2013, 30(2): 43–46. doi: 10.3969/j.issn.1001-5620.2013.02.013 HE Zhenkui. Strong inhibition and sealing water based drilling fluid technology for deviated section of shale horizontal[J]. Drilling Fluid & Completion Fluid, 2013, 30(2): 43–46. doi: 10.3969/j.issn.1001-5620.2013.02.013
[6]	常德武,蔡记华,岳也,等. 一种适合页岩气水平井的水基钻井液[J]. 钻井液与完井液, 2015, 32(2): 47–51. doi: 10.3969/j.issn.1001-5620.2015.02.012 CHANG Dewu, CAI Jihua, YUE Ye, et al. A water base mud for shale gas horizontal well[J]. Drilling Fluid & Completion Fluid, 2015, 32(2): 47–51. doi: 10.3969/j.issn.1001-5620.2015.02.012
[7]	陈庚绪,刘奥,王茜,等. 用于页岩气井的强抑制防塌高性能水基钻井液体系[J]. 断块油气田, 2018, 25(4): 529–532. CHEN Gengxu, LIU Ao, WANG Qian, et al. High inhibition and anti-sloughing water-based drilling fluid system for shale gas horizontal wells[J]. Fault-Block Oil & Gas Field, 2018, 25(4): 529–532.
[8]	吕开河,王树永,刘天科,等. 由一种多功能处理剂和盐配成的新型水基钻井液[J]. 钻井液与完井液, 2009, 26(2): 26–27. doi: 10.3969/j.issn.1001-5620.2009.02.007 LYU Kaihe, WANG Shuyong, LIU Tianke, et al. A study on a new water based drilling fluid[J]. Drilling Fluid & Completion Fluid, 2009, 26(2): 26–27. doi: 10.3969/j.issn.1001-5620.2009.02.007
[9]	KUANG Peijing, CHEN Nan, FENG Chuanping, et al. Construction and optimization of an iron particle-zeolite packing electrochemical-adsorption system for the simultaneous removal of nitrate and by-products[J]. Journal of the Taiwan Institute of Chemical Engineers, 2018, 86: 101–112. doi: 10.1016/j.jtice.2018.02.023
[10]	LI Miao, FENG Chuanping, ZHANG Zhenya, et al. Treatment of nitrate contaminated water using an electrochemical method[J]. Bioresource Technology, 2010, 101(16): 6553–6557. doi: 10.1016/j.biortech.2010.03.076
[11]	KALARUBAN M, LOGANATHAN P, KANDASAMY J, et al. Enhanced removal of nitrate in an integrated electrochemical-adsorption system[J]. Separation and Purification Technology, 2017, 189: 260–266. doi: 10.1016/j.seppur.2017.08.010
[12]	RANA P, MOHAN N, RAJAGOPAL C. Electrochemical removal of chromium from wastewater by using carbon aerogel electrodes[J]. Water Research, 2004, 38(12): 2811–2820. doi: 10.1016/j.watres.2004.02.029
[13]	许毓,刘光全,邓皓,等. 高性能水基钻井液废物不落地处理先导试验[J]. 油气田环境保护, 2017, 27(3): 19–20. doi: 10.3969/j.issn.1005-3158.2017.03.006 XU Yu, LIU Guangquan, DENG Hao, et al. Pilot test of high performance water-based drilling fluid waste treatment[J]. Environmental Protection of Oil & Gas Fields, 2017, 27(3): 19–20. doi: 10.3969/j.issn.1005-3158.2017.03.006
[14]	谢水祥,任雯,乔川,等. 可实现废弃水基钻井液再生利用的电化学吸附法[J]. 天然气工业, 2018, 38(3): 76–80. doi: 10.3787/j.issn.1000-0976.2018.03.009 XIE Shuixiang, REN Wen, QIAO Chuan, et al. An electrochemical adsorption method for the reuse of waste water-based drilling fluids[J]. Natural Gas Industry, 2018, 38(3): 76–80. doi: 10.3787/j.issn.1000-0976.2018.03.009
[15]	OOI T Y, YONG E L, DIN M F M, et al. Optimization of aluminium recovery from water treatment sludge using response surface methodology[J]. Journal of Environmental Management, 2018, 228: 13–19.
[16]	ZHANG Hui, LI Yanli, WU Xiaogang. Statistical experiment design approach for the treatment of landfill leachate by Photoelectro-Fenton process[J]. Journal of Environmental Engineering, 2011, 138(3): 278–285.
[17]	JUNG K W, AHN K H. Dual purpose recovered coagulant from drinking water treatment residuals for adjustment of initial pH and coagulation aid in electrocoagulation process[J]. Environmental Technology, 2016, 37(13): 1605–1617. doi: 10.1080/09593330.2015.1122096

施引文献

资源附件(0)

图(8) / 表(2)

计量

文章访问数: 1214
HTML全文浏览量: 407
PDF下载量: 55
被引次数: 0

1. 静态推靠机械式垂钻工具研制思路
1.1 工具结构
1.2 工作原理
2. 环形动静盘阀结构及流道设计
2.1 动静盘阀间摩擦阻力计算
2.2 环阀间隙的有限元计算分析
2.2.1 分析方法与湍流模型
2.2.2 模拟分析结果
3. 地面台架试验
4. 结论与建议

废弃高性能水基钻井液循环利用电吸附处理方法

作者简介: 任雯（1985—），女，四川广元人，2006年毕业于西南石油大学生物工程专业，2009年获西南石油大学化学工程专业硕士学位，高级工程师，主要从事石油石化固体废物处理与资源化利用技术研究。E-mail：renwen@cnpc.com.cn

计量

出版历程

Electro-Sorption Treatment Method for Waste High Performance Water-Based Drilling Fluid

1. 静态推靠机械式垂钻工具研制思路

1.1 工具结构

1.2 工作原理

2. 环形动静盘阀结构及流道设计

2.1 动静盘阀间摩擦阻力计算

2.2 环阀间隙的有限元计算分析

2.2.1 分析方法与湍流模型

2.2.2 模拟分析结果

3. 地面台架试验

4. 结论与建议

计量

出版历程

目录

1. 静态推靠机械式垂钻工具研制思路

1.1 工具结构

1.2 工作原理

2. 环形动静盘阀结构及流道设计

2.1 动静盘阀间摩擦阻力计算

2.2 环阀间隙的有限元计算分析

2.2.1 分析方法与湍流模型

2.2.2 模拟分析结果

3. 地面台架试验

4. 结论与建议

作者简介:
任雯（1985—），女，四川广元人，2006年毕业于西南石油大学生物工程专业，2009年获西南石油大学化学工程专业硕士学位，高级工程师，主要从事石油石化固体废物处理与资源化利用技术研究。E-mail：renwen@cnpc.com.cn