A Dynamic Prediction Method for Segmental Flow Performance in Horizontal Wells Based on Node Networks
-
摘要:
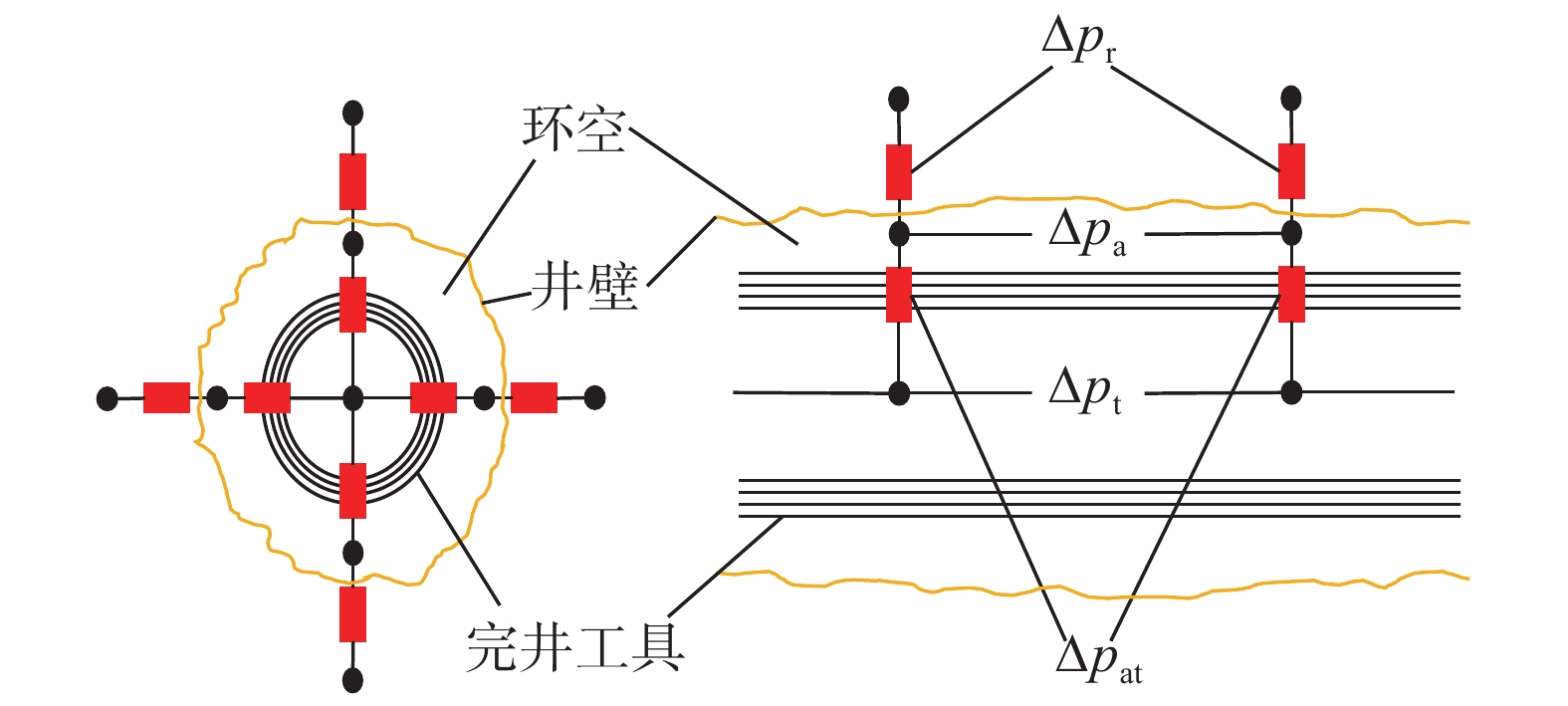
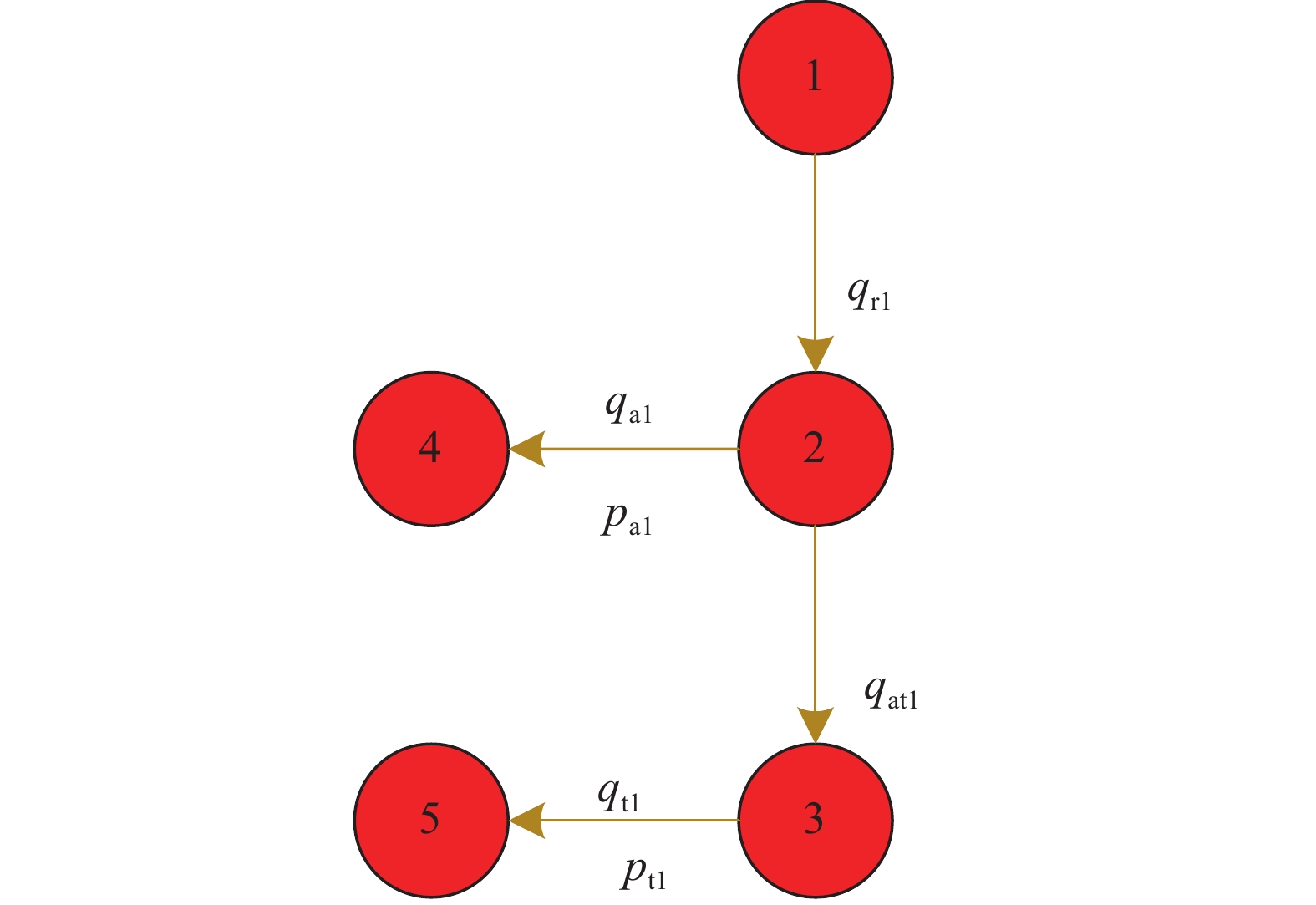
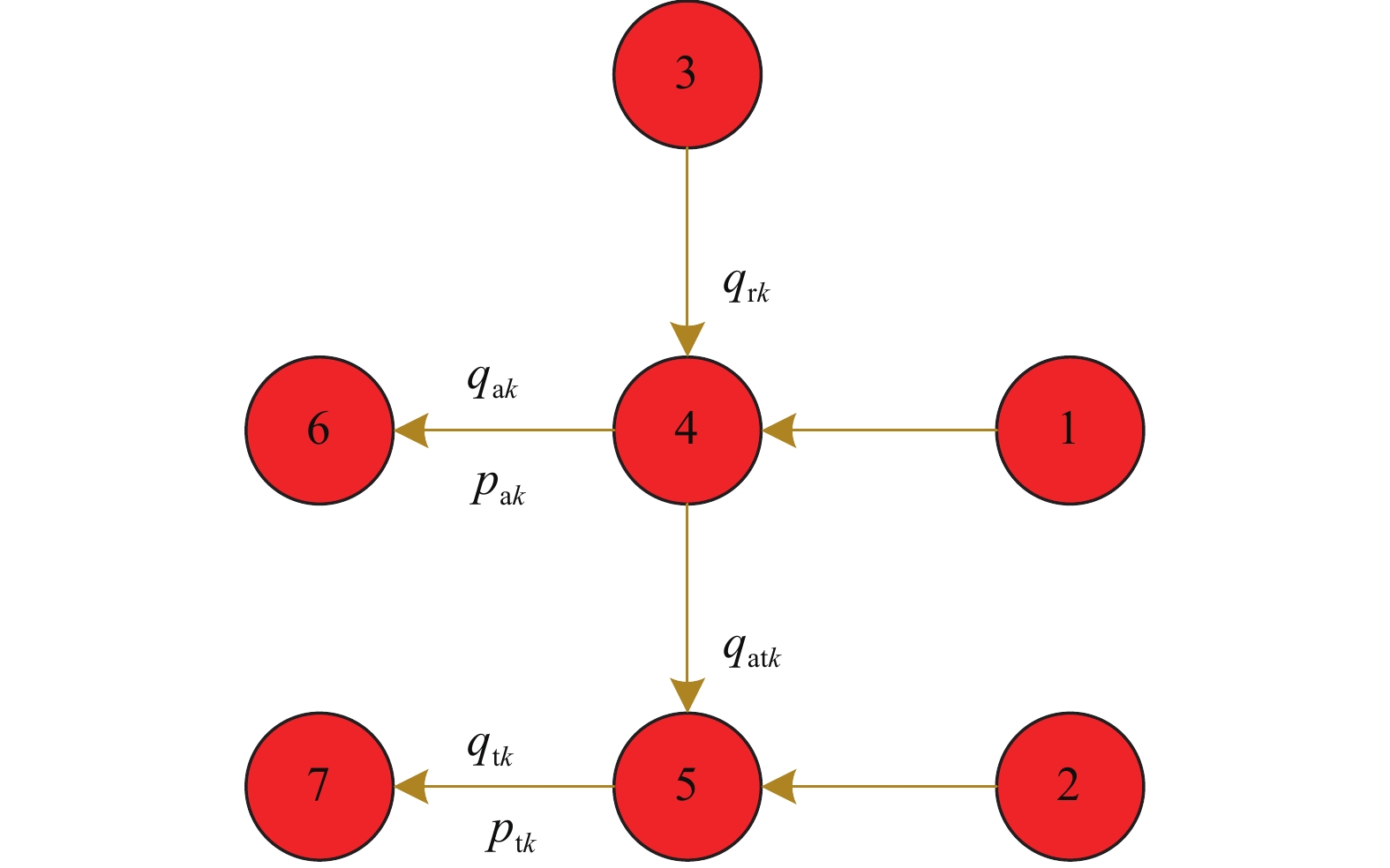
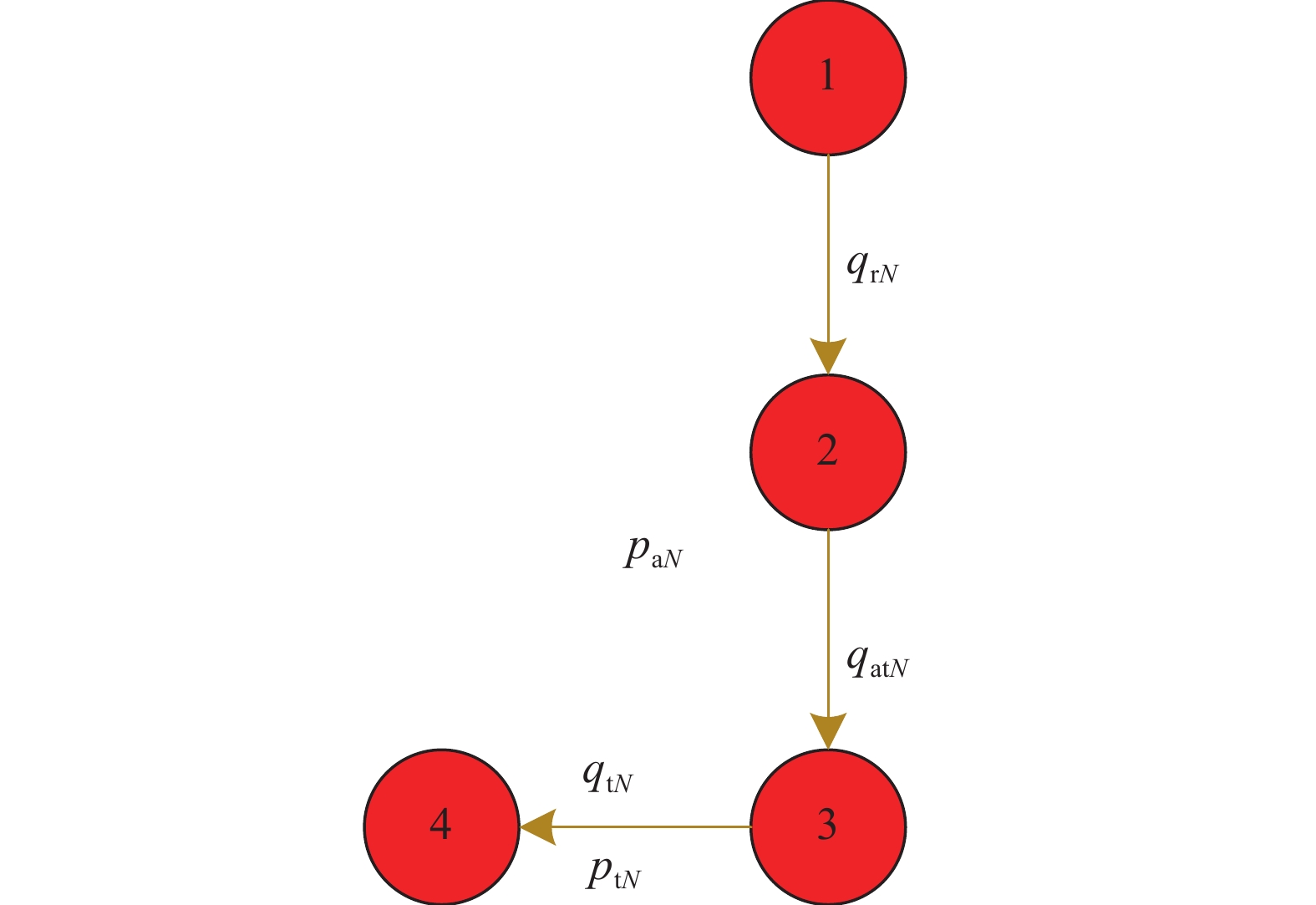
随着水平井分段完井技术的发展，完井结构变得越来越复杂，为了准确模拟水平井分段完井流入剖面，研究了基于节点网络的水平井分段流入剖面预测方法。将完井结构简化为由地层、井壁与完井工具间的环空、完井工具构成的水平井井筒网络，基于物质守恒原理和动量守恒定理，建立了各类流动桥的压降模型；用桥流动指数来表征流体流动方向，建立了耦合地层、井壁与完井工具间的环空、完井工具三者之间的流体流入剖面预测模型，并采用Newton–Raphson迭代方法进行了求解。算例分析表明，应用该方法可预测水平井复杂完井结构的环空、油管中的压力和流量分布，准确反映完井方式和完井工具对井筒流体流入剖面的影响，且具有较高的预测精度。研究认为，建立的水平井分段流入剖面模型可为完井方式选择、参数优化设计提供理论支撑。
Abstract:The dynamic prediction of segmental flow performance in horizontal wells is the basis for analyzing the adjustment effect of wellbore fluid inflow in different completion methods and the production performance of different well sections. The completion structure can be simplified into a three-layer node network composed of the formation, the annulus between borehole wall and completion tools, and completion tools. Based on the principle of mass conservation and the theorem of momentum conservation, the pressure drop model of various flow bridges was established. The bridge flow index was used to characterize the direction of fluid flow, and with the performance prediction model of the fluid flow in the coupling formation, the above mentioned annulus and the completion tools were further established. Finally, the Newton–Raphson iterative method was used to find the solution. The analysis on the calculation example showed that this model is able to predict the annulus, pressure and flow distribution in the tubing in horizontal wells with complex completion structure, and it can effectively reflect the impact of completion mode and completion tools on the fluid flow performance of the wellbore, with higher prediction precision. The established model can provide theoretical supports for the selection of segmental completion method and parameters for best practices for the optimization design of horizontal wells.
-
塔河油田碳酸盐岩缝洞型油藏与普通砂岩油藏不同，储集空间类型多样、形态差异较大，非均质性极强[1]。该油田开发初期主要依靠天然能量开采，随着开发不断进行，天然能量出现不足，采出能力开始下降，注水开发是初期解决该问题的最有效方法，但进入注水开发后期，储层经过长时间注水后，油水界面升高，驱油效果逐渐变差[2-6]。为此，进行了碳酸盐岩缝洞型油藏气水复合驱技术研究。该技术是在长时间注水后，改为注入氮气，注入的氮气会聚集在储集体高部位的阁楼体内[5-8]，将阁楼体内的剩余油油置换出来，但是由于缺乏横向驱动力，剩余油可能会大量富集在注采井网的井间；于是，在当前注气井网条件下，需再次注水增加横向水驱动力，提高井间剩余油的动用程度，从而改善碳酸盐岩缝洞型油藏的开发效果。该技术在塔河油田 4 区 7 个注采井组进行了现场应用，并获得良好的增产效果。
1. 碳酸盐岩缝洞型油藏特征
塔河油田奥陶系碳酸盐岩缝洞型油藏发育于新疆塔里木盆地沙雅隆起阿克库勒凸起的西南部，油藏埋深5 400.00～7 600.00 m，储集空间主要为溶蚀孔洞、大型洞穴和溶蚀裂缝，储集体主要为裂缝–溶洞型和裂缝–孔洞型，部分区域奥陶系一间房组地层发育微裂缝[9]。其中洞穴和孔洞的储集性能最好，裂缝既是储集空间，又是流体流动的主要通道，流体流动以管流为主[10-11]。各类岩溶体储层空间展布具有极强的非均质性，油气水运移规律复杂。
2. 气水复合驱油开发模式研究
2.1 气水复合驱油机理
在利用多属性地震资料描述储集体形态特征的基础上，通过刻蚀玻璃的方法建立了一套20 mm×30 mm的缝洞储集体物理模拟模型，该模型设计为裂缝–溶洞型储集体，孔隙度为18%。利用该模型进行气水复合驱油物理模拟试验，先注入试验用油，待模型空腔充满试验用油，再注水进行水驱，待出口已经完全出水后再注入氮气，注入一定量氮气后再次注水。试验过程中观察不同阶段模型内流体的运移情况，结果见图1。从图1可以看出，该模型在充满试验用油经水驱后，顶部的7、8号储集体内仍存在大量剩余油（见图1（a））；对其进行气驱，7、8号储集体内的剩余油被驱替到水驱通道上（见图1（b）），再次进行水驱，注入水将水驱通道上的剩余油从出口端驱替出（见图1（c））。由此可知缝洞型油藏气水复合驱油机理：氮气作为纵向驱动力，向下驱替缝洞体顶部剩余油，将剩余油驱替至水驱通道上，注入水作为横向驱动力，形成二次水驱。
![]()
图 1 复杂缝洞模型气水复合驱油流体运移情况Figure 1. Fluids migration of gas-water composite flooding in a complex fracture-cave model2.2 气水复合驱开发方式
在认识气水复合驱油机理的基础上，利用地震资料刻画井洞关系，根据生产动态识别注采井之间的连通通道，明确剩余油分布，针对不同剩余油分布特征构建了4种井组模式（见图2）：对于水驱通道在含油高度内的“阁楼油”，构建了注入井先注气、后注水的常规协同模式，为单方向一注一采的模式；对于水驱失效的多井区域的“阁楼油”，构建了注入井注气、周边邻井注水的栅状协同模式；对于出现气窜的井组，构建了换向协同模式；对于失效或未见效并且水驱通道在含油高度外的“阁楼油”，构建了注入井注气后先调流封堵水通道、再注水的调剖协同模式。
2.3 气水复合驱井网设计
主要依托岩溶背景及储层展布特征，根据基础井组模式有针对性地构建气水复合立体井网，如图3所示。对于风化壳岩溶，其展布面积广，多向连通条件好，构建面状注采井网；对于断溶体、古河道储层展布方向性强，连通特征表现为带状连通或线性连通，分别建立带状井网和线状井网[5]。
![]()
图 3 气水复合平面井网构建示意Figure 3. Schematic on the construction of the gas-water composite planar well pattern纵向上，根据井间通道路径长短、构造高低、规模大小等因素配置井网。对于有利驱替路径为陡构造、短路径、规模较小的山梁、断溶体或暗河等，如果采用低注高采井网很容易发生气窜，而采用高注低采井网则可以发挥作用集中、见效快和控制气窜的优势；有利驱替路径为缓构造、长路径，阁楼储集体靠近注入井，可以采用低注高采井网以提高驱替效率。
总体而言，需要根据通道的规模确定采用高注低采井网还是低注高采井网：短路径、小通道采用高注低采井网，以气驱为主，水驱为辅，以预防水窜；长路径、大通道采用低注高采井网，以水驱为主，气驱为辅，以提高气驱效率。实践中，2种纵向井网模式对不同规模的通道均有其优势。
2.4 气水复合驱参数设计
根据历史注水水驱效果确定水驱可动用空间，对比累计注气体积与水驱可动用空间判断通道内剩余油的再次充满程度，根据充满程度确定水驱历史等效阶段，用等效阶段的历史注水强度指导气水复合驱参数设计。
气水复合驱的作用过程分为2部分：1）垂向上，注入气将“阁楼油”驱至水驱可动用空间；2）横向上，注入水进入水驱可动用空间将油驱至受效井。注入气不断垂向驱油，关键是如何形成有效的横向水驱。根据历史注水水驱效果确定水驱可动用空间，通过对比累计注气体积与水驱可动用空间判断通道内剩余油的再次充满程度，根据剩余油充满程度确定水驱历史等效阶段，再根据等效阶段历史注水强度设计气水复合驱参数。理想驱替模型中，注采比应为1∶1，注入水前缘突破前的注水量等于增油量，注水过程中纵向上大量分水，少部分水形成了有效横向驱替。水驱结束时生产井总增油量即为有效横向水量，即水驱可驱扫空间总量。具体计算步骤（见图4）如下：
![]()
图 4 气水复合驱参数设计流程Figure 4. Flow chart of gas-water composite flooding parameters design1）确定水驱可动用空间体积。对于具有完整的水驱见效至失效阶段的注采井组，认为井间水驱可动用空间体积即水驱采油量的地下体积。
2）确定水驱可动用空间的充满程度。首先根据累计注入气量的地下体积与气驱采油量的地下体积的差，求出水驱通道中剩余油的体积；然后计算水驱可动空间的充满程度，即水驱通道剩余油体积与水驱可动用空间体积之比。
3）对应注水水驱等效阶段。利用等效原理，把任意气驱阶段对应的充满程度在水驱阶段找到对应相等充满程度的时间节点。
4）类比当时注水强度。通道充满程度相同时，注水受效日注水量为Qt。
5）确定目前的注水强度。设计目前的注水量QM≥Qt，即气水复合阶段要提供足够的横向驱动力驱动注入气顶替至水驱可动用空间内的剩余油，此时不需要考虑注水强度过大再次发生水窜的风险，因为单元注气阶段不同于注水水驱阶段，“阁楼油”可反复进入水驱通道。
3. 现场应用
气水复合驱技术在塔河油田4区7个注采井组进行了现场应用，均获得良好的增产效果，井组产油量平均提高86.0 t，累计增产油量1.3×104 t，且增油效果不断改善。下面以TK428CH–TK408井组为例，介绍气水复合驱技术的应用情况。
3.1 TK428CH–TK408井组概况
TK428CH井是注水兼注气井，TK408井是采油井，井组平面特征是沿山梁发育的风化壳岩溶，纵向特征为平缓山梁，注气路径长，“阁楼油”靠近注入井，采用低注高采井网（如图5所示）。
![]()
图 5 TK428CH–TK408井组地震属性资料与储集体刻画Figure 5. Seismic attribute data and reservoir bodies characterization of the TK428CH–TK408 well group3.2 注入参数设计
1）确定水驱可动用空间。水驱可动用空间等于前期受效增油量，该井组经历了完整的水驱阶段，水驱通道内的原油被驱替得较为彻底，因此该井组水驱增油量的地下体积等于水驱可动用空间的体积，通过计算该井组水驱可动用空间体积为5.47×104 m3。
2）判断水驱通道剩余油富集程度。该井累计注气5.70×104 m3，累计增油3.81×104 m3，通道内剩余油1.89×104 m3，水驱可动用空间充满程度为34.0%。
3）类比相同充满程度的水驱强度。当水驱阶段通道内剩余油充满程度为34.0%时，水驱处于效果变差阶段，此阶段注水量为300 m3/d，因此目前该井组合理注水量至少需要达到300 m3/d，连续注水。
4）现场注采调整及效果。调整前TK428CH井累计注气2.8×104 m3见效，后期效果出现变差趋势，计算水驱通道剩余油充满程度34.0%，水驱通道内仍富集大量剩余油，需要加强水驱动用水驱通道内的剩余油，于是TK428CH井恢复注水，并且将注水量提高至300 m3/d，TK408井生产效果改善，日增油量稳定在30 t。
4. 结论与建议
1）针对水驱和气驱无法有效动用塔河油田缝洞型碳酸盐岩油藏高部位剩余油的问题，根据其储层特征及剩余油分布特征，研究形成了气驱替油、水驱提供横向驱动力的气水复合驱技术。
2）现场应用表明，气水复合驱技术可以实现塔河油田缝洞型碳酸盐岩油藏高部位剩余油的有效动用，改善开发效果。
3）目前气水复合驱参数的设计是基于历史水驱效果进行的，还处于半定量阶段，建议进一步研究，通过地质建模和数值模拟实现定量计算。
-
![]()
图 2 水平井井筒网络节点结构示意
Figure 2. Schematic diagram of the network node structure in the horizontal wellbore
![]()
图 3 第1段网络结构及未知参数分布
Figure 3. Network structure and unknown parameter distribution of the first segment
![]()
图 4 第k段网络结构及未知参数分布
Figure 4. Network structure and unknown parameter distribution of the kth segment
![]()
图 5 第N段网络结构及未知参数分布
Figure 5. Network structure and unknown parameter distribution of the Nth segment
![]()
图 6 完井方法1的井筒节点网络模型计算结果
Figure 6. The calculation results of wellbore node network model for completion method 1
-
[1] MAALOUF C B, ZIDAN M, UIJTTENHOUT M, et al. Responsive design of inflow control devices completions for horizontal wells[R]. SPE 188794, 2017.
[2] ABDULLAYEV A, KEDIA R, URAKOV A, et al. Optimization of recovery using intelligent completions in intelligent fields(Russian)[R]. SPE 188993, 2017.
[3] 韩来聚. 胜利油田钻井完井技术新进展及发展建议[J]. 石油钻探技术, 2017, 45(1): 1–9. HAN Laiju. The latest progress and suggestions of drilling and completion techniques in the Shengli Oilfield[J]. Petroleum Drilling Techniques, 2017, 45(1): 1–9.
[4] 杨智光. 大庆油田钻井完井技术新进展及发展建议[J]. 石油钻探技术, 2016, 44(6): 1–10. YANG Zhiguang. The latest proposals for the advancement and development of drilling and completion technology in the Daqing Oilfield[J]. Petroleum Drilling Techniques, 2016, 44(6): 1–10.
[5] JOSHI S D. Augmentation of well productivity using slant and horizontal wells[R]. SPE 15375, 1986.
[6] BABU D K, ODEH A S. Productivity of a horizontal well[R]. SPE 18298, 1989.
[7] ELGAGHAH S A, OSISANYA S O, TIAB D. A simple productivity equation for horizontal wells based on drainage area concept[R]. SPE 35713, 1996.
[8] FURUI K, ZHU D, HILL A D. A rigorous formation damage skin factor and reservoir inflow model for a horizontal well[J]. SPE Production & Facilities, 2003, 18(3): 151–157.
[9] DIKKEN B J. Pressure drop in horizontal wells and its effect on production performance[J]. Journal of Petroleum Technology, 1990, 42(11): 1426–1433. doi: 10.2118/19824-PA
[10] OZKAN E, SARICA C, HACIISLAMOGLU M, et al. Effect of conductivity on horizontal well pressure behavior[R]. SPE 24683, 1992.
[11] IHARA M, KIKUYAMA K, MIZUGUCHI K. Flow in horizontal wellbores with influx through porous walls[R]. SPE 28485, 1994.
[12] 周生田, 张琪. 水平井筒压降计算方法[J]. 石油钻采工艺, 1997, 19(1): 53–59. ZHOU Shengtian, ZHANG Qi. Calculating method of pressure drop in horizontal wellbore[J]. Oil Drilling & Production Technology, 1997, 19(1): 53–59.
[13] OUYANG Liangbiao, ARBABI S, AZIZ K. General wellbore flow model for horizontal, vertical, and slanted well completions[J]. SPE Journal, 1998, 3(2): 124–133. doi: 10.2118/36608-PA
[14] CLEMO T. Flow in perforated pipes: a comparison of models and experiments[R]. SPE 89036, 2006.
[15] OUYANG Liangbiao, AZIZ K. A simplified approach to couple wellbore flow and reservoir inflow for arbitrary well configurations[R]. SPE 48936, 1998.
[16] PENMATCHA V R, AZIZ K. Comprehensive reservoir/wellbore model for horizontal wells[J]. SPE Journal, 1999, 4(3): 224–234. doi: 10.2118/57194-PA
[17] 刘想平, 郭呈柱, 蒋志祥, 等. 油层中渗流与水平井筒内流动的耦合模型[J]. 石油学报, 1999, 20(3): 82–86. LIU Xiangping, GUO Chengzhu, JIANG Zhixiang, et al. The model coupling fluid flow in the reservoir with flow in the horizontal wellbore[J]. Acta Petrolei Sinica, 1999, 20(3): 82–86.
[18] 黄世军, 程林松, 赵凤兰, 等. 阶梯水平井生产段油藏渗流与井筒变质量管流的耦合模型[J]. 水动力学研究与进展(A辑), 2005, 20(4): 463–471. HUANG Shijun, CHENG Linsong, ZHAO Fenglan, et al. The flow model coupling reservoir percolation and variable mass pipe flow in production section of the stepped horizontal well[J]. Journal of Hydrodynamics(Series A), 2005, 20(4): 463–471.
[19] 庞伟, 陈德春, 张仲平, 等. 非均质油藏水平井分段变密度射孔优化模型[J]. 石油勘探与开发, 2012, 39(2): 214–221. PANG Wei, CHEN Dechun, ZHANG Zhongping, et al. Segmentally variable density perforation optimization model of horizontal wells in heterogenic reservoirs[J]. Petroleum Exploration and Development, 2012, 39(2): 214–221.
[20] NEYLON K, REISO E, HOLMES J A, et al. Modeling well inflow control with flow in both annulus and tubing[R]. SPE 118909, 2009.
[21] 王庆, 刘慧卿, 张红玲, 等. 油藏耦合水平井调流控水筛管优选模型[J]. 石油学报, 2011, 32(2): 346–349. WANG Qing, LIU Huiqing, ZHANG Hongling, et al. An optimization model of completion strings with inner-located nozzle in horizontal wells coupled with reservoirs[J]. Acta Petrolei Sinica, 2011, 32(2): 346–349.
[22] 庞伟. 酸性气藏深井产能试井方法[J]. 油气井测试, 2018, 27(2): 67–72. PANG Wei. Deliverability test method for deep sour gas wells[J]. Well Testing, 2018, 27(2): 67–72.
[23] 刘成文, 李兆敏. 锥形喷嘴流量系数及水力参数的理论计算方法[J]. 钻采工艺, 2000, 23(5): 1–3. doi: 10.3969/j.issn.1006-768X.2000.05.001 LIU Chengwen, LI Zhaomin. A theoretical calculation method for flow rate coefficient and hydraulic parameters of conical nozzle[J]. Drilling & Production Technology, 2000, 23(5): 1–3. doi: 10.3969/j.issn.1006-768X.2000.05.001
下载:
计量
- 文章访问数: 10691
- HTML全文浏览量: 5430
- PDF下载量: 48
