Effects of the Inner Pipe Rotation and Rheological Parameters on the Axial and Tangential Velocity Profiles and Pressure Drop of Yield Power-Law Fluid in Eccentric Annulus
-
Abstract:
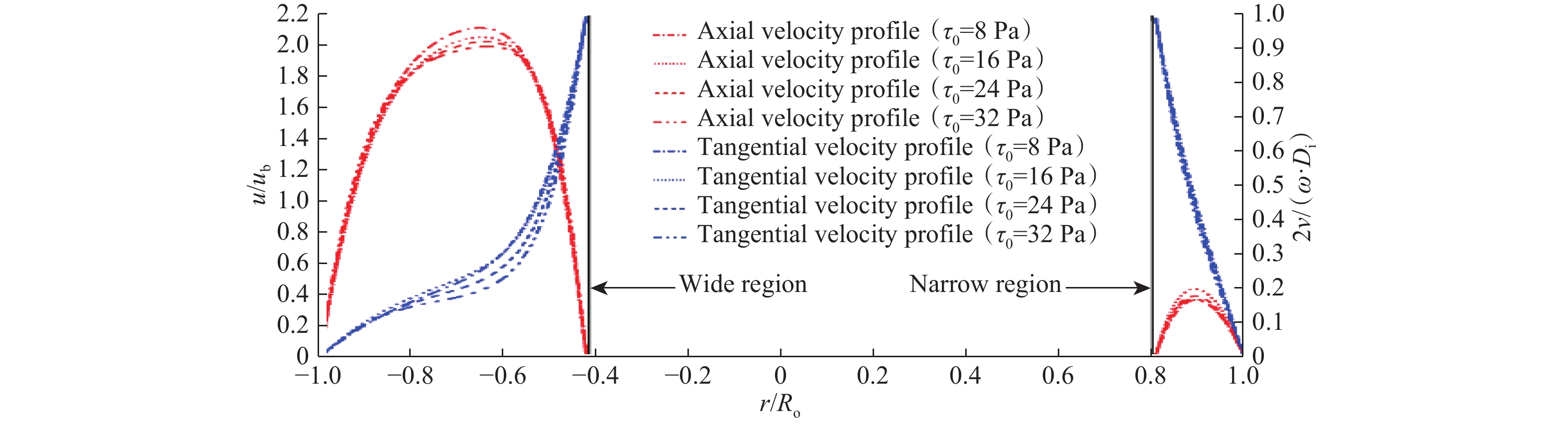
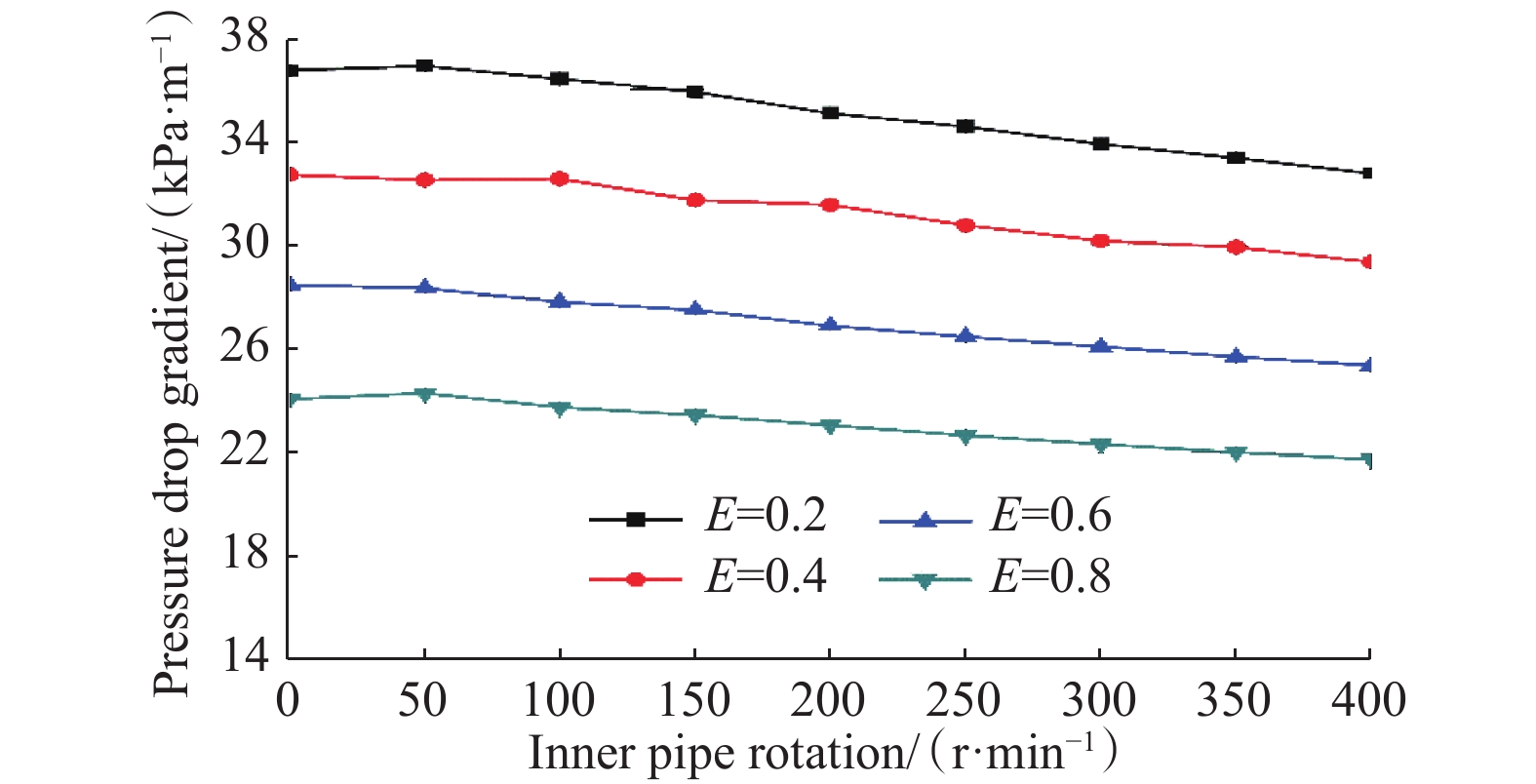
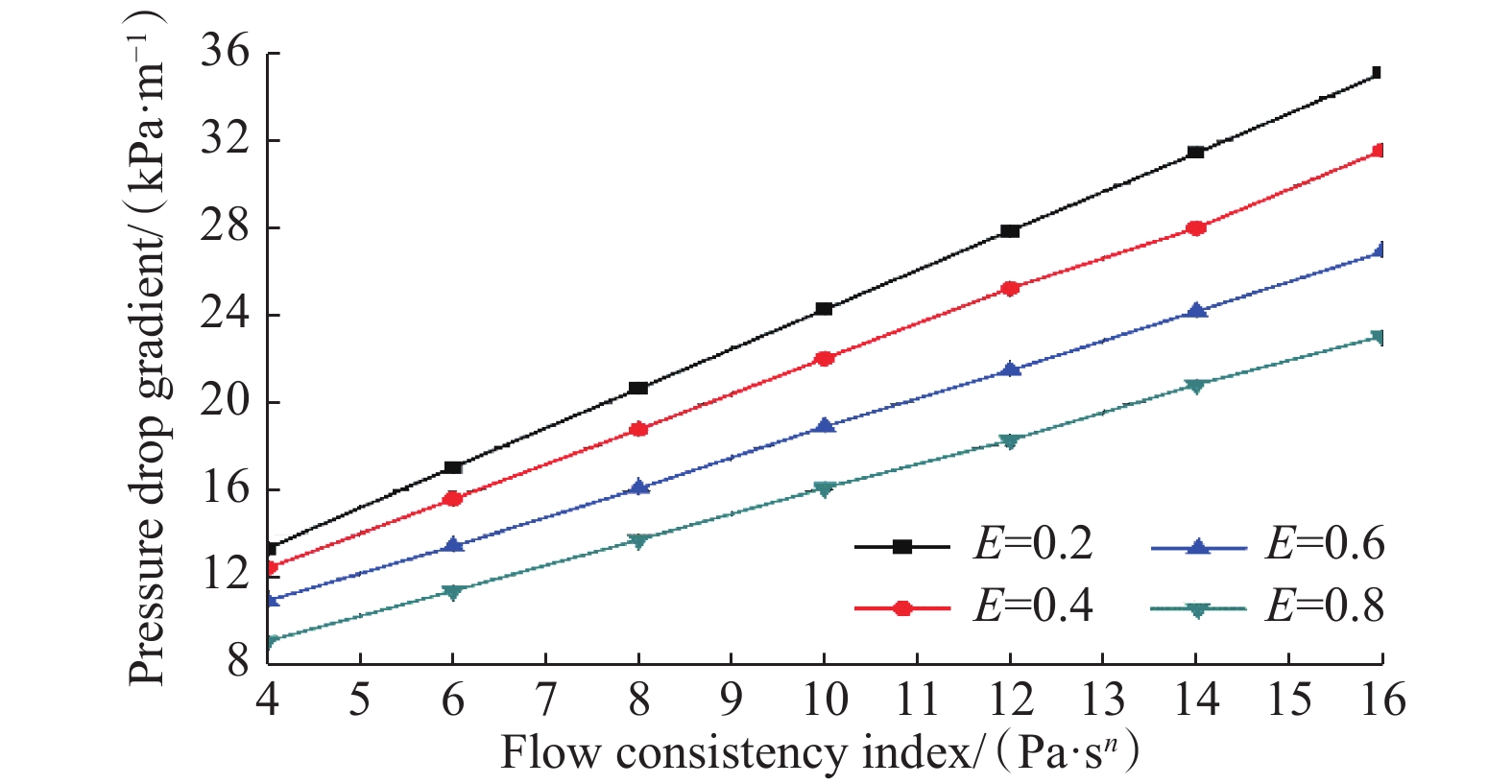
Drilling fluid mostly behaves as non-Newtonian fluid and it can be modelled by the Herschel-Bulkley model, which is also called yield power-law (YPL). This model provides accurate results for a wide range of shear rate. In the present paper, a numerical study of the Herschel-Bulkley fluid through the eccentric annulus (E=0.5) was performed for the laminar flow regime using finite volume method (FVM). Effect of the inner pipe rotation and rheology parameters (yield stress τ0, consistency index K and behavior index n) on the axial and tangential velocity profiles and pressure drop gradient were studied. Results showed that increasing the inner pipe rotation from 100 to 400 rpm induces an increase of 120 % of the maximum axial velocity. Low value of the behavior index (n=0.2) causes the appearance of the secondary flow in the wide region of the annulus. The variation of the inner pipe rotation and rheological parameters of the Herschel-Bulkley fluid have a negligible effect on the tangential velocity profile in the wide region of the eccentric annulus. Furthermore, It was observed that the increase of the inner pipe rotation from 0 rpm to 400 rpm causes a decrease of 10% of pressure drop gradient of yield power-law fluid for all eccentric annulus (E=0.2, E=0.4, E=0.6 and E=0.8).
摘要:Herschel-Bulkley模型（即屈服幂率模型）可用于研究非牛顿流体的流动特性，并能在大范围剪切速率条件下得到准确的预测结果。为此，采用有限体积方法（FVM），研究了内部管柱旋转及流变参数（屈服应力τ0、稠度系数K和流性指数n）对偏心环空（E=0.5）中Herschel-Bulkley流体层流区域的轴向、切向速度剖面与压降梯度的影响。研究结果表明，内部管柱转速从100 r/min增加至400 r/min时，会引起最大轴向速度增加，增幅为120%；较低的流性指数（n=0.2）会引起偏心环空宽区域出现二次流；内部管柱转速及流变参数的变化对偏心环空宽区域切向速度剖面有不良影响；内部管柱转速从0增加至400 r/min时，会引起不同偏心环空（E=0.2, 0.4, 0.6和0.8）内幂率流体压降梯度降低，降低幅度为10%。
-
-
![]()
Figure 4. Axial and tangential velocity profiles for various inner pipe rotations (τ0=32 Pa, K=16 Pa·s n, n=0.32)
![]()
Figure 5. Axial and tangential velocity profiles for various yield stresses (ω = 131.84 r/min, K=16 Pa·s n, n=0.43)
![]()
Figure 6. Axial and tangential velocity profiles for various consistency indexes (ω = 131.84 r/min, τ0=32 Pa, n=0.43)
![]()
Figure 7. Axial and tangential velocity profiles for various behavior indexes (ω = 131.84 r/min, τ0=32 Pa, K=16 Pa·s n)
![]()
Figure 8. Effect of the pipe rotation on pressure drop gradient for different eccentricities (Re = 12.05, τ0 = 32 Pa, K = 16 Pa·s n, n = 0.43)
![]()
Figure 9. Effect of the yield stress on pressure drop gradient for different eccentricities (Re = 12.05~14.10, ω = 200 r/min, K = 16 Pa·s n, n = 0.43).
![]()
Figure 10. Effect of the flow consistency index on pressure drop gradient for different eccentricities (Re = 12.05~30.66, ω = 200 r/min, τ0 = 32 Pa, n = 0.43).
-
[1] WHITTAKER A. Theory and application of drilling fluid hydraulics[M]. Boston: International Human Resources Development Corporation, 1985.
[2] COUSSOT P, PIAU J M. On the behavior of fine mud suspensions[J]. Rheologica Acta, 1994, 33(3): 175–184. doi: 10.1007/BF00437302
[3] NOUAR C, DESAUBRY C, ZENAIDI H. Numerical and experimental investigation of thermal convection for a thermodependent Herschel-Bulkley fluid in an annular duct with rotating inner cylinder[J]. European Journal of Mechanics-B/Fluids, 1998, 17(6): 875–900. doi: 10.1016/S0997-7546(99)80018-1
[4] HUSSAIN Q E, SHARIF M A R. Numerical modeling of helical flow of viscoplastic fluids in eccentric annuli[J]. AIChE Journal, 2000, 46(10): 1937–1946. doi: 10.1002/aic.690461006
[5] VIEIRA NETO J L, MARTINS A L, ATAÍDE C H, et al. The effect of the inner cylinder rotation on the fluid dynamics of non-Newtonian fluids in concentric and eccentric annuli[J]. Brazilian Journal of Chemical Engineering, 2014, 31(4): 829–838. doi: 10.1590/0104-6632.20140314s00002871
[6] OFEI T N, IRAWAN S, PAO W. Flow profile distribution in narrow annuli using modified yield power-law fluid model[C]//AWANG M, NEGASH B M, MD AKHIR N A, et al. ICIPEG 2014. Singapore: Springer, 2015: 209–217.
[7] AHMED R M, MISKA S Z. Experimental study and modeling of yield power-law fluid flow in annuli with drillpipe rotation[R]. SPE 112604, 2008.
[8] HANSEN S A, STERRI N. Drill pipe rotation effects on frictional pressure losses in slim annuli[R]. SPE 30488, 1995.
[9] OZBAYOGLU E M, SORGUN M. Frictional pressure loss estimation of non-Newtonian fluids in realistic annulus with pipe rotation[R]. SPE 141518, 2010.
[10] BIRD R B, STEWART W E, LIGHTFOOT E N. Transport phenomena[M]. Manhattan: John Wiley & Sons Inc., 2002.
[11] MADLENER K, FREY B, CIEZKI H K. Generalized reynolds number for non-Newtonian fluids[J]. Progress in Propulsion Physics, 2009, 1: 237–250.
[12] CENGEL Y A. Fluid mechanics[M]. India: Tata McGraw-Hill Education, 2010.
-
期刊类型引用(15)
1. 冯永超，李大雷. 泾河油田页岩油储层井壁失稳机理研究. 石油地质与工程. 2024(01): 122-126 . 
百度学术
2. 汪海阁，常龙，卓鲁斌，席传明，欧阳勇. 中国石油陆相页岩油钻井技术现状与发展建议. 新疆石油天然气. 2024(03): 1-14 . 百度学术
3. 余文帅，苏强，孟鐾桥，夏连彬，李亚天，谭天一. 天府气田致密气水平井二开一趟钻钻井关键技术. 天然气勘探与开发. 2024(06): 35-44 . 百度学术
4. 秦春，刘纯仁，李玉枝，王治国，陈文可. 苏北断块页岩油水平井钻井提速关键技术. 石油钻探技术. 2024(06): 30-36 . 本站查看
5. 袁建强. 济阳坳陷页岩油多层立体开发关键工程技术. 石油钻探技术. 2023(01): 1-8 . 本站查看
6. 赵文庄，李晓黎，周雄兵，杨慧壁，杨赟，刘克强. 陇东页岩油大平台开发钻完井关键技术. 复杂油气藏. 2023(01): 7-12 . 百度学术
7. 赵廷峰，叶雨晨，席传明，吴继伟，史玉才. 七段式三维水平井井眼轨道设计方法. 石油钻采工艺. 2023(01): 25-30 . 百度学术
8. 孙鑫，刘礼军，侯树刚，戴彩丽，杜焕福，王春伟. 基于页岩油水两相渗流特性的油井产能模拟研究. 石油钻探技术. 2023(05): 167-172 . 本站查看
9. 迟建功. 大庆古龙页岩油水平井钻井技术. 石油钻探技术. 2023(06): 12-17 . 本站查看
10. 汪海阁，周波. 致密砂岩气钻完井技术进展及展望. 天然气工业. 2022(01): 159-169 . 百度学术
11. 魏志红，刘若冰，魏祥峰，陈斐然，刘珠江，王道军. 四川盆地复兴地区陆相页岩油气勘探评价与认识. 中国石油勘探. 2022(01): 111-119 . 百度学术
12. 王国娜，张海军，孙景涛，张巍，曲大孜，郝晨. 大港油田大型井丛场高效钻井技术优化与应用. 石油钻探技术. 2022(02): 51-57 . 本站查看
13. 苏兴华，詹胜，康芳玲. 面向工程约束的大井丛轨道防碰优化模块设计. 信息系统工程. 2022(05): 72-75 . 百度学术
14. 严圣飞. 靖中北小三开型三维水平井快速钻井技术. 化学工程与装备. 2022(09): 137-138 . 百度学术
15. 秦春，刘纯仁，陈文可，唐玉华，曹林云. 苏北盆地HY1HF井钻完井关键技术. 复杂油气藏. 2022(03): 17-23 . 百度学术
其他类型引用(1)
下载:
计量
- 文章访问数: 964
- HTML全文浏览量: 336
- PDF下载量: 79
- 被引次数: 16
