2. 中国石油钻井工程技术研究院, 北京 102206 ;
3. 中国石油塔里木油田分公司油气工程研究院, 新疆库尔勒 841000
2. CNPC Drilling Research Institute, Beijing, 102206, China ;
3. CNPC Tarim Oil Field Oil and Gas Engineering Institute, Korla, Xinjiang, 841000, China
我国非常规油气资源丰富,但开发较晚,且因常规钻井技术存在成本高、效率低的问题,使目前非常规油气的产量在全部油气产量中的占比仍不到5%。与常规钻井相比,连续管钻井(coiled tubing drilling,CTD)技术具有安全、高效、低成本等优势,在国外已广泛应用于常规和非常规油气的开发,若国内在开发非常规油气资源时能应用CTD技术,必能实现低成本、高效率[1-3]。因此,CTD技术在我国有较好的应用前景。不过,由于连续管属柔性管柱,无法从地面进行旋转定向,需应用井下定向装置[3-5]。
自20世纪90年代以来,国外多家石油技术服务公司开始进行连续管钻井定向装置的研究,具有代表性的如Weatherford、Sperry-Sun和Schlumberger等石油技术服务公司的液压定向装置以及Baker Hughes公司的电液驱动定向装置。液压定向装置依靠泵循环单方向旋转工具面,每次可旋转角度20°~45°,需开关泵数十次才能达到目标工具面角度,且调整工具面时钻头需提离井底,效率低[6]。电液驱动定向装置依靠连续管内置电缆供电,可双向连续旋转工具面,能够实时控制井眼轨迹,但其结构复杂,研制难度大,其核心技术只被国外少数石油技术服务公司所掌握。为了推动CTD技术在我国油气开发中的应用,有必要研制连续管钻井电液定向装置(electric-hydraulic orienter,EHO)。为此,笔者在设计连续管钻井EHO结构的基础上,提出了连续管钻井EHO工具面调整方法[5-7],并通过连续管钻水平井实例验证了该方法的可行性,分析了其效果。
1 EHO的结构及原理CTD井下工具主要由连续管、连接器、各类接头、随钻测量工具、电液定向装置和钻头等部件组成,如图 1所示。其中,EHO上接随钻测量工具,下接弯螺杆和钻头。

|
| 图 1 CTD井下工具组合示意 Fig.1 Bottom-hole assemblies (BHA) for CTD 1.连续管;2.连接器;3.电力信息接头;4.电开关接头;5.连接器;6.电力性能接头;7.随钻测量工具;8.EHO;9.弯螺杆;10.钻头 |
EHO可依靠连续管中的电缆供电,其内置构件将电能转换为液压能,再将液压能转换为旋转动能输出,从而使该装置能够双向连续旋转工具面,实时控制井眼轨迹。基于该思路,笔者对EHO进行了结构设计,包括动力转换单元、监测控制单元和扭矩输出单元3部分。动力转换单元包括微型电动机、传动装置、微型液压泵和油箱;监测控制单元包括电磁换向阀和角度位移传感器;扭矩输出单元包括双级螺旋液压缸、芯轴和输出轴,其中液压缸中的双级螺旋机构包括固定螺母、滑动螺母和螺旋芯轴。EHO的基本结构和工作原理如图 2所示。
|
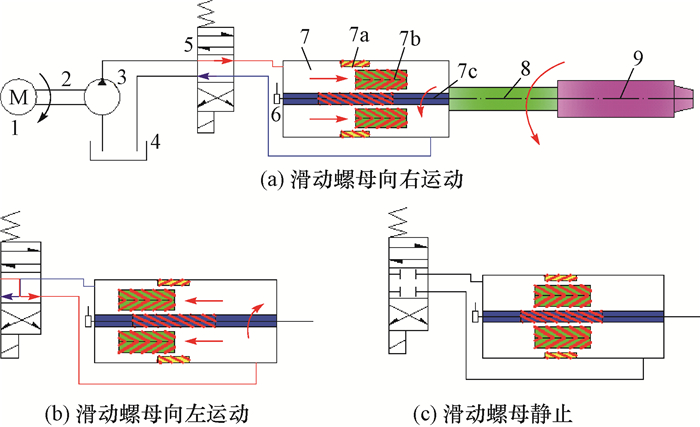
| 图 2 EHO的基本结构及工作原理示意 Fig.2 Structure and working principles of EHO 1.微型电动机;2.传动装置;3.微型液压泵;4.油箱;5.电磁换向阀;6.角度位移传感器;7.双级螺旋液压缸;7a.固定螺母;7b.滑动螺母;7c.螺旋芯轴;8.心轴;9.输出轴 |
EHO的主要设计参数:最大外径为101.6 mm,长度为2.55 m,液压缸滑动螺母行程为110 mm,双级螺旋机构导程角为70°,最大输出扭矩为1 300 N·m,输出轴旋转范围为0°~360°,输出轴转速为1.5~3.0(°)/s,输出轴旋转精度为1.0°。
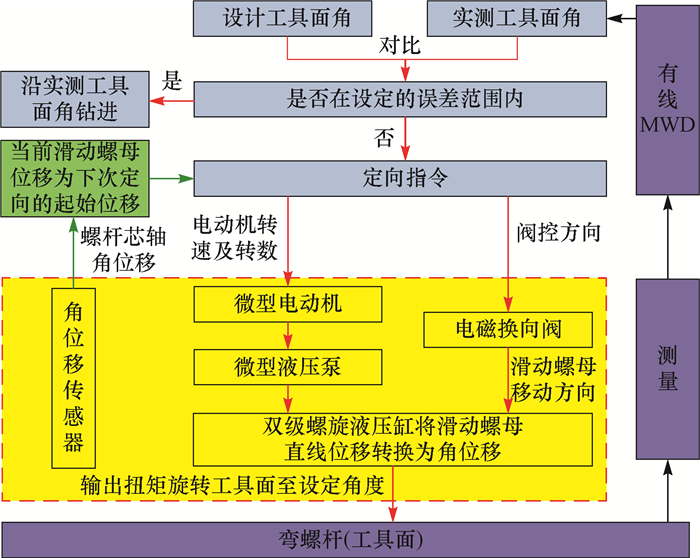
连续管钻井过程中,由于井下存在反扭矩,弯螺杆的工具面会发生变动,在钻遇复杂地层时这种变动尤为严重。有线MWD可将实时测得的工具面角信息通过连续管中的电缆上传到地面控制系统进行分析对比,若当前工具面角与设计工具面角之间的偏差在允许范围内(例如不大于5°),则继续沿当前工具面角钻进;若偏差超过允许值,由地面控制系统通过连续管中的电缆对定向装置发出定向指令,确保沿设计轨道钻进。EHO的工具面闭环检测控制系统如图 3所示(红色虚线框代表电液定向装置)。
|
| 图 3 EHO的工具面角闭环检测控制系统 Fig.3 Closed-loop detection and control system for toolface adjustment of EHO |
工具面角闭环检测控制系统的具体定向过程为:连续管钻井过程中,地面系统通过连续管中内置电缆给EHO中的微型电动机供电,微型液压泵在电动机的带动下向双级螺旋液压缸供油,使液压缸中的双级螺旋机构相互作用,带动螺旋芯轴输出扭矩,从而旋转工具面。同时,地面控制系统指示定向装置中的电磁换向阀控制液压油的流量、流向,从而控制双级螺旋液压缸中滑动螺母的运动位移和方向。若滑动螺母在一个行程内(0~110 mm)往复轴向移动,相应地,工具面可在0°~360°内旋转。滑动螺母向右运动时,工具面顺时针旋转,如图 2(a)所示(从左往右看);反之,滑动螺母向左运动时,工具面逆时针旋转,如图 2(b)所示;当工具面角度达到设计值时,利用电磁换向阀的中位机能将工具面锁紧在当前位置,如图 2(c)所示。在该过程中,角位移传感器实时记录螺旋芯轴的旋转角度,将角度信息通过连续管中的电缆传至地面控制系统,由地面控制系统得出相应的滑动螺母位移,记录定向完成时的当前位移,为下次定向准备。当工具面再次发生变动超过偏差允许值时,重复上述定向过程。
EHO克服了液压定向装置精度低、效率低的不足:首先,其通过双级螺旋传动机构双向转动工具面,定向精度高(取决于双级螺旋机构的加工配合精度);其次,其通过连续管中内置的电缆传输电力及信号,动作指令迅速,定向效率更高。
2 工具面角调整控制由于连续管是柔性管柱,受地层特性参数及工艺操作参数变化的影响,在CTD过程中工具面易偏离设计工具面角[8-10],若偏差过大,则实钻井眼轨迹将超出设计窗口。因此,需实时调整工具面角,使其接近设计的工具面角。按照斜面圆弧理论,需保持工具面角在斜面圆弧内接近设计值[11-13]。
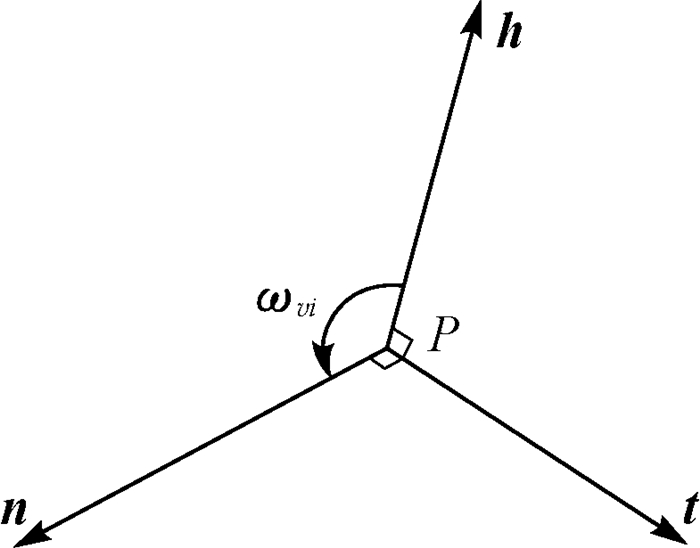
2.1 工具面角计算根据空间圆弧轨迹矢量描述方法,对于斜面圆弧轨迹上任意一点P,工具面角ωvi如图 4所示(h为井眼高边矢量,n为圆弧内法线矢量,t为井眼方向矢量)[14-16]。
|
| 图 4 工具面角示意 Fig.4 Tool face angle |
斜面圆弧轨迹上井深增量为ΔL的任意点处的设计工具面角ωvi为:
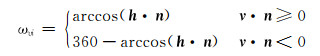
|
(1) |
其中
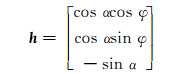
|
(2) |
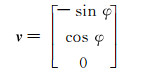
|
(3) |
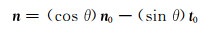
|
(4) |
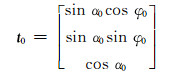
|
(5) |
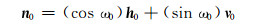
|
(6) |
式中:v为方位垂向矢量;α为设计井斜角,(°);φ为设计方位角,(°);θ为圆弧弯曲角,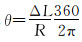
则工具面所需调整角度Δωi为:
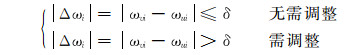
|
(7) |
式中:δ为偏差设定值,(°);ωui为实测工具面角,(°)。
CTD过程中,每钻进ΔL(ΔL≤5 m)时[16],由地面系统根据式(7)判断实测工具面角与设计工具面角的偏差是否在设定值之内,从而确定是否需要调整工具面角,以保证沿设计井眼轨道钻进。
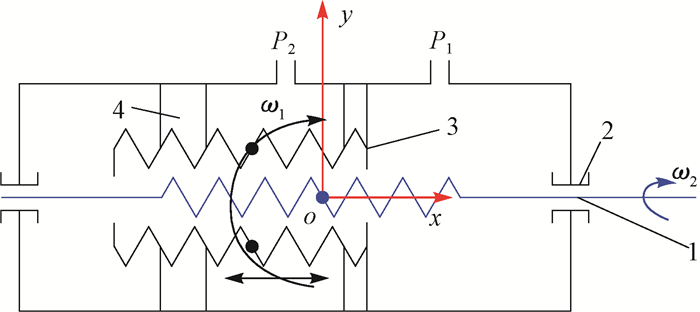
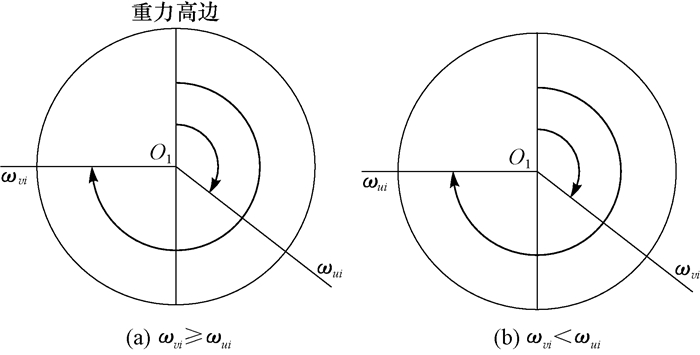
2.2 工具面角的传递与控制双向调整工具面实质上是依靠控制双级螺旋液压缸中滑动螺母的往复轴向移动来执行的,控制滑动螺母的运动位移即可控制工具面角的调整量与调整方向,故笔者分析了双级螺旋液压缸的滑动螺母运动位移与工具面角调整量、调整方向之间的关系,滑动螺母运动位移如图 5所示(P1为滑动螺母内侧与螺旋芯轴的导程,mm;P2为滑动螺母外侧与固定螺母的导程,mm;ω1为滑动螺母角速度,rad/s;ω2为螺旋芯轴角速度,rad/s),工具面角的调整如图 6所示。
|
| 图 5 双级螺旋传动机构示意 Fig.5 Dual-screw transmission mechanism 1.螺旋芯轴;2.推力轴承;3.滑动螺母;4.固定螺母 |
|
| 图 6 工具面调整示意 Fig.6 Schematic diagram for tool face adjustment |
从图 5可以看出,滑动螺母内侧与螺旋芯轴配合,滑动螺母外侧与固定螺母配合,固定螺母通过紧固螺钉固定在液压缸缸体上,该螺旋传动单元为单自由度机构。根据三者之间的几何位置关系,可得角位移方程为:
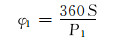
|
(8) |
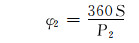
|
(9) |
工具面旋转角度为:
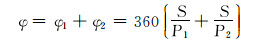
|
(10) |
若工具面旋转角度为0°~360°,则:
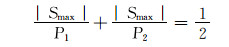
|
(11) |
滑动螺母的行程为:
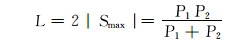
|
(12) |
式中:S为滑动螺母的轴向位移,mm;φ1为滑动螺母相对于固定螺母的角位移,(°);φ2为螺旋芯轴相对于滑动螺母的角位移,(°);φ为螺旋芯轴相对于固定螺母的角位移, (°);Smax为滑动螺母的最大轴向位移,mm;L为滑动螺母的行程,mm。
结合图 5与图 6,推导滑动螺母运动位移与工具面角的调整量、调整方向之间的函数关系。在图 5中,由于螺旋芯轴轴向固定,故以其中心为原点,建立平面直角坐标系xOy。双级螺旋液压缸的滑动螺母内侧和螺旋芯轴的旋向均为右旋,当滑动螺母右移时,可顺时针方向调整工具面(从上部朝井底方向看);反之,滑动螺母左移时,可逆时针方向调整工具面。调整工具面过程中,将滑动螺母的移动设定为“就近原则”,以提高效率。“就近原则”是指:当液压缸的滑动螺母质心位移xi>0时,首先判断滑动螺母右移能否达到目标工具面角,若无法达到(双级螺旋机构的行程所限),则左移滑动螺母;当滑动螺母质心位移xi < 0时,判断滑动螺母左移能否达到设计工具面,若无法达到,则右移滑动螺母。
滑动螺母运动位移与工具面的调整关系如下:
1) 如图 5、图 6(a)所示,若|Δωi|>δ且ωvi≥ωui,即Δωi>0且xui>0时,按照“就近原则”,若
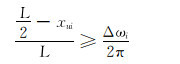
|
(13) |
此时滑动螺母需右移。顺时针调整工具面至工具面角等于设计值,滑动螺母位移为:
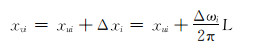
|
(14) |
若
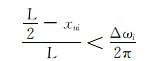
|
(15) |
此时滑动螺母需左移。逆时针调整工具面至工具面角等于设计值,滑动螺母位移为:
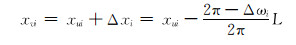
|
(16) |
2) 如图 5、图 6(a)所示,若|Δωi|>δ, Δωi>0且xui < 0时,根据“就近原则”,若
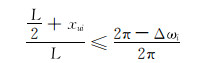
|
(17) |
此时滑动螺母需左移。逆时针调整工具面至工具面角等于设计值,滑动螺母位移为:
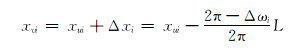
|
(18) |
若
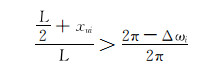
|
(19) |
此时滑动螺母需右移。顺时针调整工具面至工具面角等于设计值,滑动螺母位移为:
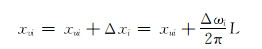
|
(20) |
3) 如图 5、图 6(b)所示,若|Δωi|>δ,Δωi < 0且xui>0时,按照“就近原则”,若
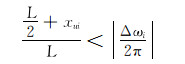
|
(21) |
此时滑动螺母需右移。顺时针调整工具面至工具面角等于设计值,滑动螺母位移为:
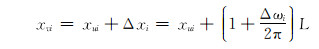
|
(22) |
若
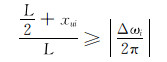
|
(23) |
此时滑动螺母需左移。逆时针调整工具面至工具面角等于设计值,滑动螺母位移为:
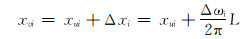
|
(24) |
4) 如图 5、图 6(b)所示,若|Δωi|>δ,Δωi < 0且xui < 0时,按照“就近原则”,若
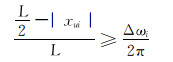
|
(25) |
此时滑动螺母需左移。逆时针调整工具面至工具面角等于设计值,滑动螺母位移为:
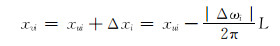
|
(26) |
若
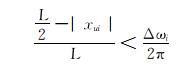
|
(27) |
此时滑动螺母需左移。逆时针调整工具面至工具面角等于设计值,滑动螺母位移为:
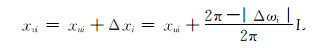
|
(28) |
式中:xui为滑动螺母当前位移,mm;Δxi为滑动螺母位移变化量,mm。
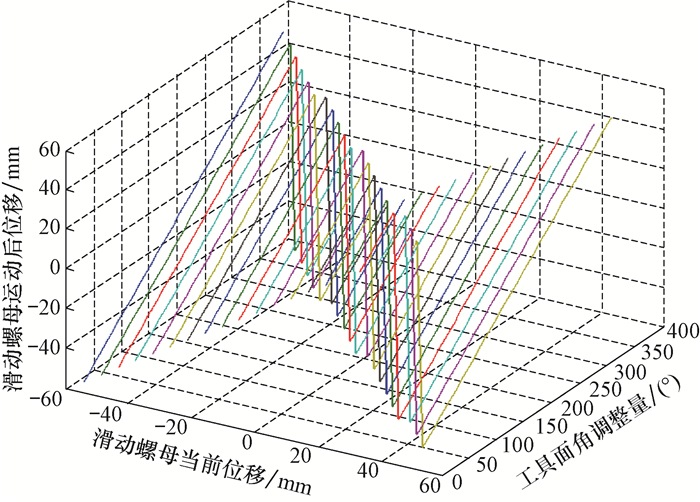
根据式(13)-式(28)可得出滑动螺母当前位移变化时,滑动螺母运动位移与工具面角调整量之间的关系如图 7所示,滑动螺母当前位移一定时,滑动螺母运动后位移与工具面角调整量呈“折线”关系,随着工具面角调整量增大,由于滑动螺母导程所限,在单方向上的移动不能调整到目标工具面角,此时需要反方向移动滑动螺母,即出现“折线”,且在每条“折线”的两斜直线段上,滑动螺母运动后位移随工具面角调整量均呈线性增加关系;滑动螺母当前位移越大(即滑动螺母位置越靠右,见图 5),滑动螺母运动后位移“越早”出现曲折(即在工具面角调整量较小时,滑动螺母就需反方向移动以调整到目标工具面角)。
|
| 图 7 滑动螺母运动位移与工具面角调整量的关系 Fig.7 The relation between the toolface adjustment and the piston movement |
大港油田官-X12井是官195断块上的一口老井侧钻井,在井深715 m处φ139.7 mm套管内开窗,目的层为孔店组孔一段油层,为验证电液定向装置工具面调整方法的可行性及准确性,应用连续管钻井技术钻侧钻水平段,水平段设计采用斜面圆弧轨道。已知条件:1)目标点T(E, N, Z)依次为t1(400.0, 400.0, 995.0)、t2(450.0, 600.0, 1 000.5)、t3(650.0, 650.0, 995.1)、t4(872.0, 570.0, 990.0);2)弯螺杆的结构弯角为1.5°,长度为6 m;3)实测工具面角与设计轨道工具面角的偏差设定值为5°。
先按照式(1)-式(6)计算设计井眼轨道的工具面角;然后,在连续管钻井过程中,每钻进5 m对实测工具面角度与设计工具面角度进行一次对比,若|ωvi-ωui|>δ,需根据式(13)-式(28)及时调整工具面角至设计值,部分工具面调整数据见表 1。
| 目标点 | 井深增量/m | 井斜角/(°) | 方位角/(°) | 工具面角/(°) | 滑动螺母位移/mm | 滑动螺母 移动方向 |
工具面 旋转方向 |
||||||||
| 设计值 | 实测值 | 设计值 | 实测值 | 设计值 | 实测值 | 差值 | 调整前 | 调整后 | |||||||
| 1 | 0 | 87.40 | 87.43 | 343.04 | 343.15 | 29.36 | 29.27 | -0.09 | -38.100 | √ | √ | √ | |||
| 5.00 | 87.43 | 87.50 | 344.47 | 344.61 | 29.33 | 27.02 | -2.31 | -38.100 | √ | √ | √ | ||||
| 10.00 | 87.47 | 87.53 | 345.90 | 346.04 | 29.31 | 24.19 | -5.12 | -38.100 | -39.630 | 左 | 逆时针 | ||||
| 25.00 | 87.59 | 87.66 | 350.19 | 350.33 | 29.24 | 28.90 | -0.34 | -39.630 | √ | √ | √ | ||||
| 30.00 | 87.63 | 87.71 | 351.63 | 351.77 | 29.23 | 358.40 | -30.83 | -39.630 | -48.870 | 左 | 逆时针 | ||||
| 40.00 | 87.72 | 87.76 | 354.49 | 354.63 | 29.19 | 28.96 | -0.23 | -48.870 | √ | √ | √ | ||||
| | | | | | | | | | | | | ||||
| 80.00 | 88.13 | 88.28 | 5.94 | 6.13 | 29.12 | 22.58 | -6.54 | -52.140 | 53.766 | 右 | 顺时针 | ||||
| | | | | | | | | | | | | ||||
| 2 | 215.00 | 89.96 | 89.99 | 44.53 | 44.78 | 29.99 | 29.90 | -0.09 | 36.516 | √ | √ | √ | |||
| | | | | | | | | | | | | ||||
| 430.00 | 92.61 | 93.62 | 106.02 | 105.43 | 158.24 | 30.56 | -127.60 | 10.686 | -27.570 | 左 | 逆时针 | ||||
| 3 | 435.00 | 92.55 | 92.78 | 106.08 | 105.48 | 158.05 | 157.96 | -0.09 | -27.570 | √ | √ | √ | |||
| | | | | | | | | | | | | ||||
| 660.00 | 89.97 | 90.13 | 108.81 | 109.32 | 149.91 | 144.14 | -5.77 | 41.098 | 52.718 | 右 | 顺时针 | ||||
| 4 | 665.00 | 89.91 | 90.07 | 108.87 | 109.43 | 149.83 | 148.53 | -0.60 | 41.098 | √ | √ | √ | |||
| 注:“√”表示实测工具面角度与设计工具面角度在偏差设定范围内,无需调整。 | |||||||||||||||
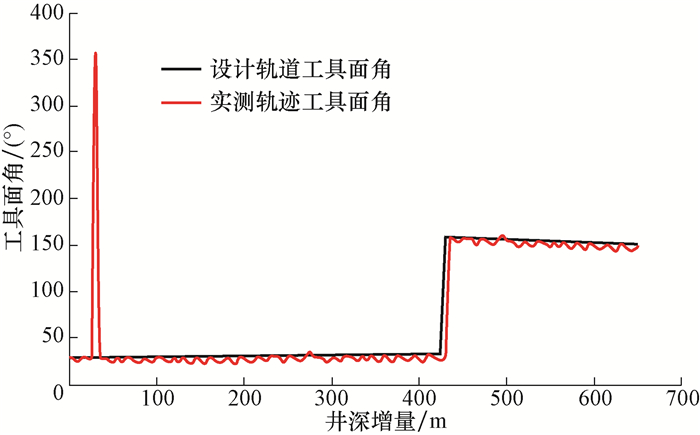
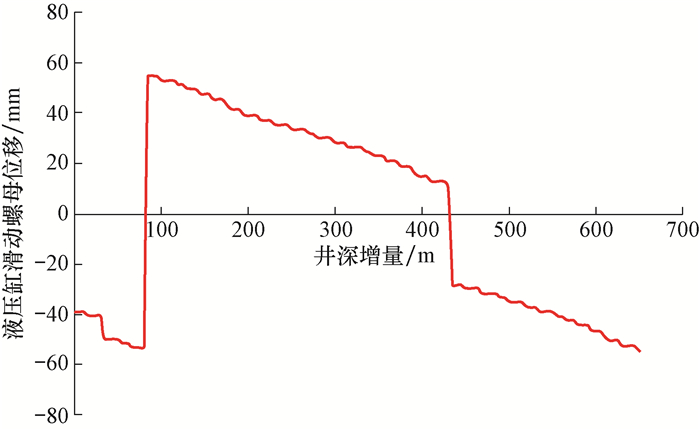
根据表3,距离目标点1井深增量10.00 m处的实测工具面角为24.19°,设计值为29.31°,由式(7)得|Δωi|=5.12°>δ。该偏差是由于CTD过程中地层反扭矩作用造成的工具面角偏差累积引起的,工具面角随井深增量的变化如图 8所示。按式(13)-式(28)及时调整工具面角,已知当前滑动螺母位移xui=-38.1 mm,调整到设计值时滑动螺母位移为xvi=-39.6 mm,滑动螺母需向左移动,逆时针调整工具面,滑动螺母位移变化如图 9所示。
|
| 图 8 工具面角随井深增量的变化 Fig.8 Changes of the tool surface angles with well depths |
|
| 图 9 液压缸滑动螺母位移随井深增量的变化 Fig.9 Changes of the hydraulic cylinder piston displacements with well depths |
井深增量为30.00 m处进行钻压与钻速关系试验,在短时间内将钻压从15 kN增大至30 kN,工具面角发生较大变动(见图 8),实测值为358.40°,而设计值为29.23°,由式(7)得|Δωi|=30.83°>δ,滑动螺母运动之后位移为-48.87 mm,滑动螺母需向左移动,逆时针调整工具面,滑动螺母位移变化如图 9所示。试验结束后,钻压恢复至15 kN。
3.3 试验3井深增量为80.00 m处,工具面角实测值为22.58°,设计值为29.12°,由式(7)得|Δωi|=6.54°>δ。当前滑动螺母位移为-52.14 mm,根据“就近原则”滑动螺母应左移,但双级螺旋机构的行程有限,此时左移无法调整到设计工具面角,按照边界条件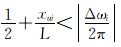
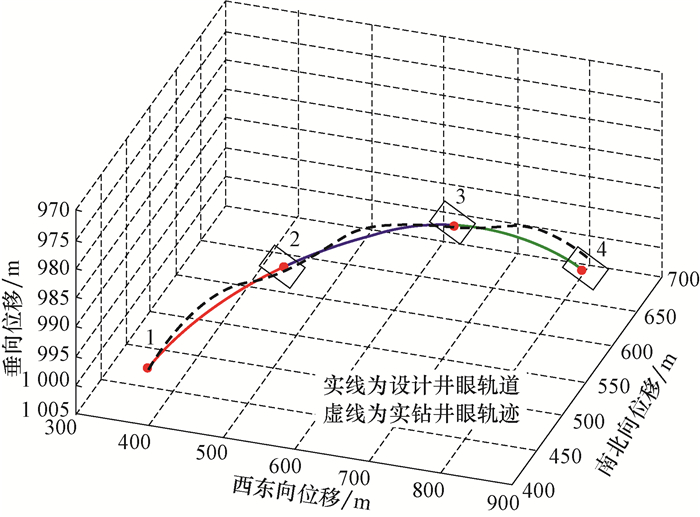
根据上述工具面调整方法,得出连续管钻水平段过程中随井深增量变化的滑动螺母位移曲线(见图 9);同时按设计井眼轨道实时调整工具面角得到的实钻井眼轨迹如图 10中虚线所示,结果显示水平段实钻井眼轨迹与设计井眼轨道接近,均在设计窗口内,在各目标点处均命中靶区,满足连续管钻井精确定向的要求。
|
| 图 10 多目标段设计轨道 Fig.10 Designed wellbore trajectory in interval with multiple targets |
1) 应用空间圆弧轨迹的矢量描述方法,建立了连续管钻井工具面角计算模型,并通过分析电液定向装置双级螺旋机构的结构特点及工具面角调整规律,得到了滑动螺母运动位移与工具面角调整量、调整方向的函数。
2) 在连续管钻井过程中,应用设计的电液定向装置及其工具面调整方法可实时连续双向调整工具面,有助于提高连续管钻井效率,利于国内连续管钻井技术的实施。
3) 电液定向装置结构设计及工具面角调整方法,为开发连续管钻井过程中电液定向装置的电液控程序奠定了基础。
| [1] |
刘清友, 瞿丹, 黎伟.
连续管钻井技术在国内非常规气开发中的应用[J]. 石油机械 , 2011, 39 (supplement 1) : 94–97, 101.
LIU Qingyou, QU Dan, LI Wei. Application of coiled tubing drilling technology in the development of unconventional gas in China[J]. China Petroleum Machinery , 2011, 39 (supplement 1) : 94–97, 101. |
| [2] |
陈朝伟, 周英操, 申瑞臣, 等.
连续管钻井减摩技术综述[J]. 石油钻探技术 , 2010, 38 (1) : 29–31.
CHEN Zhaowei, ZHOU Yingcao, SHEN Ruichen, et al. Overview of drag reducing technologies in coiled tubing drilling[J]. Petroleum Drilling Techniques , 2010, 38 (1) : 29–31. |
| [3] | HADIPUTRO B, CORSO C S, TROY T, et al.Case study:innovation application of automated drilling system with hybrid coiled tubing drilling rig excels in cost-sensitive environment[R].SPE 114597, 2008. |
| [4] | BINGHAM B.Rotationaltoolface orientation to facilitate coiled tubing target acquisition[R].SPE 62738, 2000. |
| [5] | ANDERSON D R, DOREL A, MARTIN R.A new, integrated, wireline-steerable, bottom hole assembly brings rotary drilling-like capabilities to coiled tubing drilling[R].SPE 37654, 1997. |
| [6] |
李猛, 贺会群, 张云飞, 等.
连续管钻井定向器技术现状与发展建议[J]. 石油机械 , 2015, 43 (1) : 32–37.
LI Meng, HE Huiqun, ZHANG Yunfei, et al. The status quo and development suggestion on the coiled tubing drilling orienter[J]. China Petroleum Machinery , 2015, 43 (1) : 32–37. |
| [7] | LEISING L J, NASON T.System and method for directional drilling:US 8960330[P].2015-02-24. |
| [8] | TURNER D R, HARRIS T W R, SLATER M, et al.Electric coiled tubing drilling:a smarter CT drilling system[R].SPE 52791, 1999. |
| [9] | TINKHAM S K, MEEK D E, STAAL T W, et al.Wired BHA applications in underbalanced coiled tubing drilling[R].SPE 59161, 2000. |
| [10] | ROSS M, ANYANWU O N, KLOTZ C, et al.Rib-steered motor technology:the revolutionary approach extends the coiled tubing drilling application scope[R].SPE 153573, 2012. |
| [11] |
刘修善, 王继平.
基于大地测量理论的井眼轨迹监测方法[J]. 石油钻探技术 , 2007, 35 (4) : 1–5.
LIU Xiushan, WANG Jiping. A method for monitoring wellbore trajectory based on the theory of geodesy[J]. Petroleum Drilling Techniques , 2007, 35 (4) : 1–5. |
| [12] |
韩志勇.
定向钻井设计与计算[M]. 2版. 东营: 中国石油大学出版社 ,2007 : 193 -205.
HAN Zhiyong. Design and calculation of directional drilling[M]. 2nd ed. Dongying: China University of Petroleum Press , 2007 : 193 -205. |
| [13] |
吴宏均, 令文学, 初永涛.
吉林油田浅层丛式水平井井眼轨迹控制技术[J]. 石油钻探技术 , 2011, 39 (5) : 31–34.
WU Hongjun, LING Wenxue, CHU Yongtao. Trajectory control technology for shallow cluster horizontal wells in Jilin Oilfield[J]. Petroleum Drilling Techniques , 2011, 39 (5) : 31–34. |
| [14] |
鲁港, 佟长海, 夏泊洢, 等.
空间圆弧轨迹的矢量描述技术[J]. 石油学报 , 2014, 35 (4) : 759–764.
LU Gang, TONG Changhai, XIA Boyi, et al. Vector description of spatial-arc wellbore trajectory[J]. Acta Petrolei Sinica , 2014, 35 (4) : 759–764. |
| [15] |
胡亮, 高德利.
连续管钻定向井工具面角调整方法研究[J]. 石油钻探技术 , 2015, 43 (2) : 50–53.
HU Liang, GAO Deli. Study in a method for tool face re-orientation with coiled tubing drilling[J]. Petroleum Drilling Techniques , 2015, 43 (2) : 50–53. |
| [16] |
刘修善.
井眼轨道几何学[M]. 北京: 石油工业出版社 ,2006 : 56 -77.
LIU Xiushan. Geometry of wellbore trajectory[M]. Beijing: Petroleum Industry Press , 2006 : 56 -77. |


