2. 中国石油大学(北京)石油工程学院, 北京 102249
2. College of Petroleum Engineering, China University of Petroleum(Beijing), Beijing, 102249, China
涡流排液采气是一种新型排采工艺,该工艺通过涡流工具在井筒中形成气液两相涡流流动,利用气井自身能量排液,解决井筒积液问题[1-2]。涡流排液采气工艺在美国、澳大利亚等国家进行了现场应用[3-5],在我国苏里格气田和雅克拉-大涝坝气田等多个气田也进行了现场应用[6-8]。一些气井应用涡流工具后增产效果明显,另外一些气井则未达到预期效果,说明目前涡流工具的应用存在盲目性,对涡流排液的机理和适用性认识不清。
研究人员通过物理模拟实验观测和分析了涡流工具的排液效果[9-10]。但是,目前对涡流工具螺旋角的研究较多[11-14],而关于螺旋流道宽度和密封性对排液效果影响的研究则鲜有报道。同时,目前得到的涡流工具螺旋角优化值受限于特定的实验条件,缺乏理论模型的指导,螺旋角优化结果存在很大的局限性。为此,笔者开展了涡流排液采气物理模拟实验,分析了涡流工具结构参数对排液效果的影响,以及涡流工具对临界携液流量的影响,提出并验证了最优螺旋角理论模型,以期为涡流工具的结构优化和现场应用提供理论依据。
1 实验装置排液采气涡流工具实验装置如图 1所示。模拟井筒为高8.00 m、内径60.0 mm的透明有机玻璃管。供气装置为螺杆式空气压缩机,用恒压自来水供液。气体和液体在模拟井筒底部混合后流经涡流工具。采用质量流量计计量气体流量,采用水表计量液体流量。为了准确记录井筒压降,在模拟井筒的底部至顶部共布置5个测压点。流量、温度和压力数据通过数据采集系统实时记录。由于井筒多相流受惯性力和重力的影响比黏性力大,因此取弗劳德数为实验相似准数。

|
| 图 1 涡流工具实验装置 Fig.1 Experimental facilities for the vortex tool |
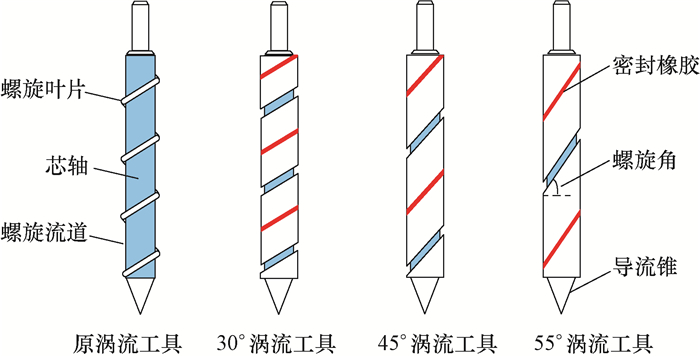
实验加工了4种不同结构的涡流工具(主要由螺旋体和导流锥组成),分别为原涡流工具、30°涡流工具、45°涡流工具和55°涡流工具(30°、45°和55°为螺旋角度),如图 2所示。原涡流工具的主要特点为螺旋流道的流动截面大,并且流道两侧没有密封,其他3种涡流工具的主要区别为螺旋角度不同。涡流工具的结构参数见表 1。
|
| 图 2 加工的涡流工具示意 Fig.2 Schematic diagram of manufactured the vortex tool |
| 工具名称 | 螺旋角/(°) | 叶片宽度/mm | 流道宽度/mm | 芯轴直径/mm | 螺距/mm | 外径/mm | 总长度/mm | 是否密封 |
| 原涡流工具 | 30 | 9 | 87 | 38 | 96 | 58 | 306 | 否 |
| 30°涡流工具 | 30 | 87 | 9 | 38 | 96 | 58 | 306 | 是 |
| 45°涡流工具 | 45 | 151 | 9 | 38 | 160 | 58 | 306 | 是 |
| 55°涡流工具 | 55 | 263 | 9 | 38 | 272 | 58 | 306 | 是 |
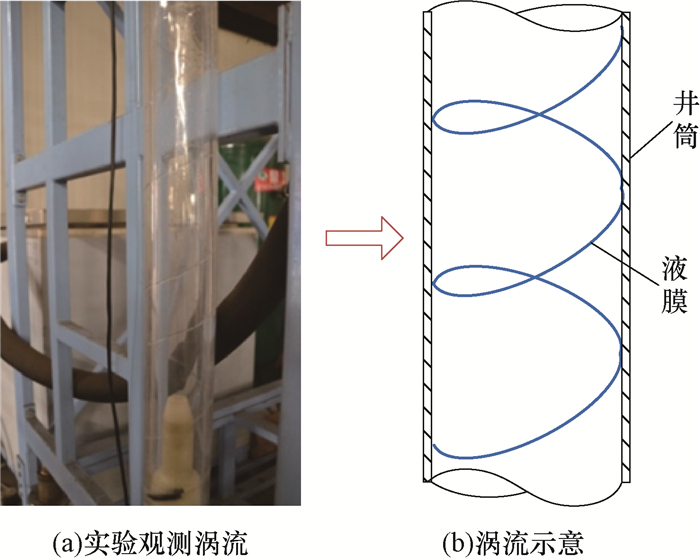
涡流工具结构合理时,流体流经涡流工具后会形成明显的涡流流动。安装45°涡流工具进行实验,观测井筒涡流流动形态,结果如图 3所示。从图 3可以看出, 流动螺旋线切线与径向方向的夹角约等于涡流工具螺旋角,液膜宽度约等于涡流工具螺旋流道槽宽。
|
| 图 3 流体流经涡流工具后的井筒涡流流动状态 Fig.3 Wellbore vortex flow state after fluid passing the vortex tool |
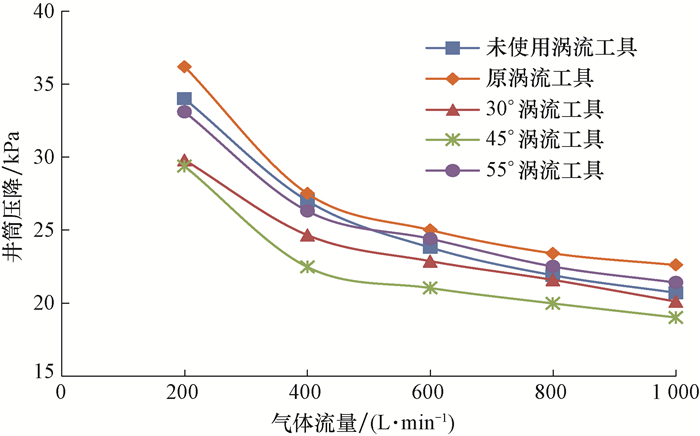
井筒无涡流工具和安装不同涡流工具时,在气体流量分别为200,400,600,800和1 000 L/min条件下,调节进入井筒的液体流量,使井底压力稳定在30 kPa左右。流动稳定后,记录井筒各测压点处的压力,得到井筒压降曲线, 如图 4所示。
|
| 图 4 不同气体流量下的井筒压降曲线 Fig.4 Wellbore pressure drop curves under different gas flow rates |
由图 4可知,30°涡流工具和45°涡流工具的井筒压降小于未使用涡流工具时的井筒压降,说明30°涡流工具和45°涡流工具可以降低井筒流动能耗,排液效果好。气体流量较小时,55°涡流工具的井筒压降略小于未使用涡流工具时的井筒压降,节能效果不明显;气体流量较大时,55°涡流工具反而对排液不利,这是因为55°涡流工具产生的离心力较小,无法有效减小流动能耗。原涡流工具的井筒压降大于未使用涡流工具时的井筒压降,排液效果最差,这是因为原涡流工具的螺旋流道过宽,对流体加速作用小,流体无法获得足够的动能;此外,流道两侧无密封,流体从涡流工具与管壁间的缝隙处向上窜流,增加了流动能耗。
气体流量较小时,与未使用涡流工具时相比,30°涡流工具和45°涡流工具的井筒压降降幅较大,排液效果较好;随着气体流量增大,气体携液能力增强,涡流工具的井筒压降降幅变小。当气体流量大于临界携液流量时,无需安装涡流工具也可依靠气体能量有效排液。
从井筒压降角度评价排液效果优劣:45°涡流工具>30°涡流工具>55°涡流工具>原涡流工具。与未使用涡流工具相比,45°涡流工具的井筒压降降幅平均为9.6%。
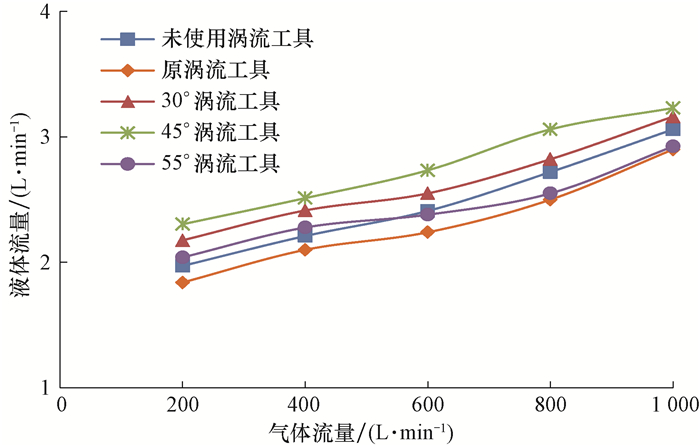
2.3 流量曲线未使用涡流工具和安装不同涡流工具时,在不同气体流量下调节进入井筒的液体流量,使井底压力稳定在30 kPa左右。流动稳定后,记录相应的液体流量,得到如图 5所示的流量曲线。
|
| 图 5 不同气体流量下的液体流量曲线 Fig.5 Liquid flow rate curves under different gas flow rates |
由图 5可知,30°涡流工具和45°涡流工具的排液量大于未使用涡流工具时的排液量,说明30°涡流工具和45°涡流工具的排液效果好。随着气体流量增大,55°涡流工具的排液量先大于未使用涡流工具时的排液量、随后小于未使用涡流工具时的排液量,说明55°涡流工具排液效果较差。原涡流工具的排液量小于未使用涡流工具时的排液量,排液效果最差。
气体流量较小时,与未使用涡流工具相比,30°涡流工具和45°涡流工具的排液量增幅较大,排液效果较好;随着气体流量增大,涡流工具排液量的增幅越来越小。当气体流量大于临界携液流量时,无需安装涡流工具也可有效排液。
从排液量角度评价排液效果优劣:45°涡流工具>30°涡流工具>55°涡流工具>原涡流工具。与未使用涡流工具相比,45°涡流工具的排液量增幅平均为12.4%。
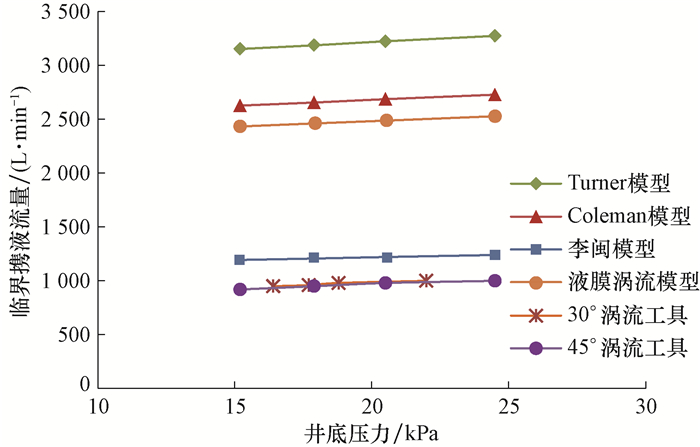
2.4 临界携液流量井筒安装45°涡流工具或30°涡流工具时,调节井口节流阀的开度,使进入井筒的气体能够将井筒中的液体全部排出,流动达到稳定。减小气体流量,直至井筒中的液膜出现明显下落,井底压力短时间内明显增大; 随后稍微增大气体流量,当井筒中的液膜保持稳定滞止状态时,对应的气体流量为临界携液流量。改变节流阀开度,重复测试,记录不同井底压力下的临界携液流量,并与理论携液流量模型计算结果[15-18]进行比较,结果见图 6。
|
| 图 6 临界携液流量曲线 Fig.6 Critical flow rate curves |
由图 6可知,45°涡流工具的临界携液流量略小于30°涡流工具的临界携液流量,并小于各理论携液流量模型计算结果。李闽模型对现场气井的积液预测精度最高,因此以李闽临界携液流量作为井筒积液的判断依据[19]。与李闽模型的临界携液流量相比,45°涡流工具的临界携液流量平均降低20.8%。因此,气体流量大于80%李闽模型临界携液流量时,应用优化后的涡流工具可以有效排液。
3 涡流工具螺旋角优化实验条件下得到的最优螺旋角受实验参数的限制,具有一定的局限性,因此需要建立具有普遍适用性的最优螺旋角理论模型,根据气井实际情况计算不同生产参数下的最优螺旋角,合理优化涡流工具。为此,利用流体动力学分析方法,建立了最优螺旋角理论模型。
3.1 最优螺旋角理论模型根据两相流体动力学理论,对井筒涡流场中的液滴进行了受力分析,并对各项作用力进行了量级比较[20],进而得到了涡流场液滴所受垂向合力(垂直向上为正方向):
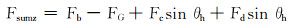
|
(1) |
式中:Fsumz为液滴所受垂向合力,N;Fb为液滴所受浮力,N;FG为液滴所受重力,N;Fc为液滴所受离心力,N;θh为涡流工具螺旋角,(°);Fd为液滴所受气体曳力,N。
式(1)中各力的表达式为:
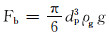
|
(2) |
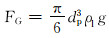
|
(3) |
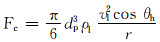
|
(4) |
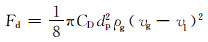
|
(5) |
式中:dp为液滴直径,m;g为重力加速度,m/s2;ρg为气相密度,kg/m3;ρl为液相密度,kg/m3;vl为液滴速度,m/s;vg为气相速度,m/s;r为液滴与管道轴心间的径向距离,m;CD为阻力系数。
将式(2)—式(5)代入式(1),并将Fsumz对θh求一阶导数和二阶导数,得到液滴所受垂向合力最大时对应的螺旋角θh0,即涡流工具最优螺旋角:
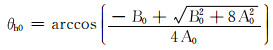
|
(6) |
其中
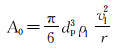
|
(7) |
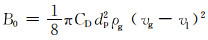
|
(8) |
式中:θh0为涡流工具最优螺旋角,(°)。
液滴直径采用涡流场最大稳定液滴直径公式计算[21],阻力系数根据不同雷诺数范围下的近似公式计算[22]。
液相流动截面约等于涡流工具螺旋流道的流动截面,则液滴速度为:
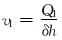
|
(9) |
式中:Ql为液相体积流量,m3/s;δ为涡流工具螺旋流道槽深,m;h为涡流工具螺旋流道槽宽,m。
气相主要以气心形式沿井筒中部向上流动,则气相流动速度为:
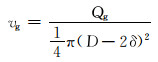
|
(10) |
式中:Qg为气相体积流量,m3/s;D为井筒直径,m。
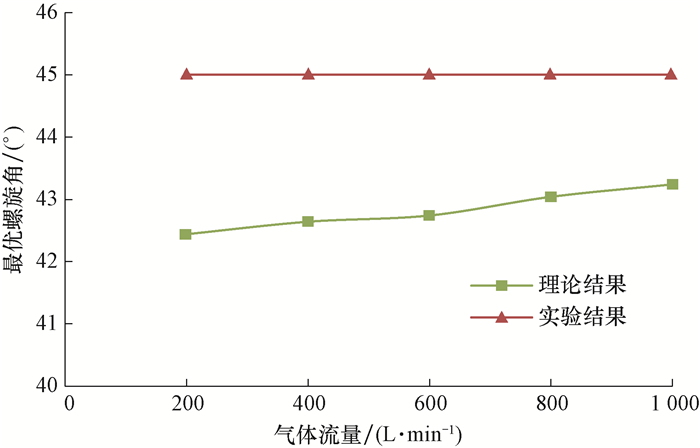
3.2 理论计算结果与实验结果比较根据实验所得的井筒压降和流量曲线结果分析可知,45°涡流工具排液效果最好,即实验最优螺旋角为45°。利用实验参数条件,根据最优螺旋角公式计算得到理论最优螺旋角,并与实验得到的最优螺旋角进行比较,结果如图 7所示。
|
| 图 7 最优螺旋角理论结果与实验结果对比 Fig.7 Results comparison of optimal helix angle by theoretical analysis and experimental study |
由图 7可知,理论最优螺旋角为42.4°~43.2°,平均为42.8°。随着气体流量增大,气体携液能力增强,无需产生较强的涡流即可排出积液,因此理论最优螺旋角逐渐增大。由于实验中加工的涡流工具数量较少,所以不同气体流量下的实验最优螺旋角均为45°。
通过分析,理论最优螺旋角与实验最优螺旋角的最大相对误差小于6%,可认为理论结果与实验结果吻合较好。因此,可根据现场井筒实际条件利用理论模型优化涡流工具螺旋角。
4 结论与建议1) 涡流工具螺旋流道两侧的密封性和流道的流动截面积对排液效果有较大影响,对螺旋流道两侧进行密封,并在较小流动阻力条件下减小流动截面积,可以提高涡流工具的排液效果。
2) 涡流工具具有一定的气体流量适用范围。当气体流量大于80%李闽模型临界携液流量时,下入涡流工具可有效排液;当气体流量大于李闽模型临界携液流量时,气体能量充足,无需下入涡流工具。
3) 建议根据现场气井实际参数条件,利用最优螺旋角理论模型优化和设计不同下入深度处涡流工具的螺旋角,以提高涡流工具的排液效果。
| [1] |
SIMPSON D A. Vortex flow technology finding new applications[J]. Rocky Mountain Oil Journal, 2003, 83(45): 4-5. |
| [2] |
陈德春, 付刚, 韩昊, 等. 气井携液用涡流工具结构参数优化[J]. 石油钻采工艺, 2016, 38(3): 400-404. CHEN Dechun, FU Gang, HAN Hao, et al. Optimization of structural parameters for fluid-carrying swirl tool in gas wells[J]. Oil Drilling & Production Technology, 2016, 38(3): 400-404. |
| [3] |
ALI A J, SCOTT S L, FEHN B. Investigation of new tool to unload liquids from stripper-gas wells[J]. SPE Production & Facilities, 2005, 20(4): 306-316. |
| [4] |
SINGH K A, SARKAR P, PRALEYA P, et al.Unconventional cyclone gas lift completion for offshore wells of Cambay Basin: a smart completion to optimize production and well intervention[R].SPE 181574, 2016. https://www.onepetro.org/conference-paper/SPE-181574-MS
|
| [5] |
ZHANG Z, LIAO R Q, LIU J. Dynamics and effective distance of gas-liquid two-phase swirling flow induced by vortex tools[J]. Advances in Mechanical Engineering, 2018, 10(9): 1-11. |
| [6] |
杨旭东, 卫亚明, 肖述琴, 等. 井下涡流工具排水采气在苏里格气田探索研究[J]. 钻采工艺, 2013, 36(6): 125-127. YANG Xudong, WEI Yaming, XIAO Shuqin, et al. Research of downhole vortex dewatering gas recovery in Sulige Gasfield[J]. Drilling & Production Technology, 2013, 36(6): 125-127. DOI:10.3969/J.ISSN.1006-768X.2013.06.37 |
| [7] |
周朝, 吴晓东, 汤敬飞, 等. 井下涡流排液采气井筒临界携液量计算[J]. 大庆石油地质与开发, 2016, 35(6): 99-103. ZHOU Chao, WU Xiaodong, TANG Jingfei, et al. Calculation of the critical liquid carry-over in the wellbore for downhole vortex dewatering gas recovery[J]. Petroleum Geology and Oilfield Development in Daqing, 2016, 35(6): 99-103. DOI:10.3969/J.ISSN.1000-3754.2016.06.018 |
| [8] |
陈德春, 姚亚, 韩昊, 等. 气井涡流排液采气工具有效作用长度[J]. 断块油气田, 2016, 23(4): 537-540. CHEN Dechun, YAO Ya, HAN Hao, et al. Effective length of vortex tools for liquid discharge in gas wells[J]. Fault-Block Oil & Gas Field, 2016, 23(4): 537-540. |
| [9] |
侯绪田, 赵向阳, 孟英峰, 等. 基于真实裂缝试验装置的液液重力置换试验研究[J]. 石油钻探技术, 2018, 46(1): 30-36. HOU Xutian, ZHAO Xiangyang, MENG Yingfeng, et al. Liquid-liquid gravity displacement test based on experimental apparatus for real fractures[J]. Petroleum Drilling Techniques, 2018, 46(1): 30-36. |
| [10] |
谢志勤. 自蔓燃化学点火火烧油层物理模拟研究[J]. 石油钻探技术, 2018, 46(3): 93-97. XIE Zhiqin. Physical simulation study of in-situ combustion by a chemical self-propagating igniter[J]. Petroleum Drilling Techniques, 2018, 46(3): 93-97. |
| [11] |
ALI A J.Investigation of flow modifying tools for the continuous unloading of wet-gas wells[D].College Station: Texas A & M University, 2003. https://oaktrust.library.tamu.edu/handle/1969.1/ETD-TAMU-2003-THESIS-A45
|
| [12] |
BOSE R.Unloading using auger tool and foam and experimental identification of liquid loading of low rate natural gas wells[D].College Station: Texas A&M University, 2007. https://core.ac.uk/display/4272789
|
| [13] |
杜汶浓.川西气田涡流排水采气工艺技术研究[D].成都: 西南石油大学, 2015. DU Wennong.Research of vortex gas drainage technology in Western Sichuan Gas Field[D].Chengdu: Southwest Petroleum University, 2015. |
| [14] |
陈德春, 韩昊, 姚亚, 等. 气井涡流工具作用效果分析与临界携液流量实验研究[J]. 天然气地球科学, 2015, 26(11): 2137-2140. CHEN Dechun, HAN Hao, YAO Ya, et al. An experimental study on the effect of the vortex tool and its influence on critical velocity[J]. Natural Gas Geoscience, 2015, 26(11): 2137-2141. DOI:10.11764/j.issn.1672-1926.2015.11.2137 |
| [15] |
TURNER R G, HUBBARD M G, DULKER A E. Analysis and prediction of minimum flow rate for the continuous removal of liquids from gas wells[J]. Journal of Petroleum Technology, 1969, 21(11): 1475-1482. DOI:10.2118/2198-PA |
| [16] |
COLEMAN S B, CLAY H B, McCURDY D G, et al. A new look at predicting gas well load-up[J]. Journal of Petroleum Technology, 1991, 43(3): 329-333. DOI:10.2118/20280-PA |
| [17] |
李闽, 郭平, 谭光天. 气井携液新观点[J]. 石油勘探与开发, 2001, 28(5): 105-106. LI Min, GUO Ping, TAN Guangtian. New look on removing liquids from gas wells[J]. Petroleum Exploration and Development, 2001, 28(5): 105-106. DOI:10.3321/j.issn:1000-0747.2001.05.031 |
| [18] |
RICHTER H J. Flooding in tubes and annuli[J]. International Journal of Multiphase Flow, 1981, 7(6): 647-658. DOI:10.1016/0301-9322(81)90036-7 |
| [19] |
周朝, 吴晓东, 刘雄伟, 等. 深层凝析气井临界携液模型优化研究[J]. 特种油气藏, 2015, 22(6): 97-100. ZHOU Chao, WU Xiaodong, LIU Xiongwei, et al. Study on optimization of critical fluid carrying model for deep condensate gas well[J]. Special Oil & Gas Reservoirs, 2015, 22(6): 97-100. DOI:10.3969/j.issn.1006-6535.2015.06.021 |
| [20] |
吴晓东, 周朝, 安永生, 等. 涡流排液采气的液滴动力学分析与螺旋角优化[J]. 天然气工业, 2016, 36(5): 45-50. WU Xiaodong, ZHOU Chao, AN Yongsheng, et al. Dynamic analysis of liquid droplet and optimization of helical angle for vortex drainage gas recovery[J]. Natural Gas Industry, 2016, 36(5): 45-50. |
| [21] |
金向红, 金有海, 王建军. 气液旋流器内液滴破碎和碰撞的数值模拟[J]. 中国石油大学学报(自然科学版), 2010, 34(5): 114-120, 125. JIN Xianghong, JIN Youhai, WANG Jianjun. Numerical simulation on breakup and collision of droplet in gas-liquid cyclone separator[J]. Journal of China University of Petroleum(Edition of Natural Science), 2010, 34(5): 114-120, 125. |
| [22] |
郭烈锦. 两相与多相流动力学[M]. 西安: 西安交通大学出版社, 2002: 342-345. GUO Liejin. Two-phase and multiphase flow mechanics[M]. Xi'an: Xi'an Jiaotong University Press, 2002: 342-345. |




