页岩气储层渗透率极低,在成岩作用、多阶段构造演化、气体赋存状态及介质尺度等方面都与常规油气藏存在较大差异,其既是烃源岩又是储集层,储层中发育大量的微纳米孔隙和干酪根有机质[1-3],是典型的原地成藏[4]。近年来,随着长水平段水平井技术和分段压裂技术的发展,非常规油气资源的开发成为可能[5-6]。页岩气储层压裂过程中容易产生裂缝网络系统[7],形成的多尺度天然裂缝-人工裂缝相互交织会在储层中形成宏观优势流动区域,影响渗流场压力和流体组分的分布。因此,复杂裂缝网络表征、页岩气渗流机理模拟方法等是国内外的研究热点[8-11]。
页岩气在岩石中以游离态和吸附态2种形式存在[12-13],并表现出黏性流、努森扩散、吸附表面扩散等4种典型流动状态[14-18]。有研究表明[19-21],页岩气藏的产能主要来自于水力裂缝网络和地层中的微裂缝微孔隙,其短期产量依赖于主裂缝,而长期产量依赖于基质部分解吸。干酪根和基质孔隙介质的渗透率极低,渗流速度极慢,建立数学模型时需要考虑不同介质之间的差异,因此,如何准确地表征基质内部的传质规律对描述页岩气产能至关重要[22]。目前,关于表征裂缝性介质流动的数学模型主要有等效连续介质模型[23-24]、双重介质模型[25]、多重连续介质模型[26]、双孔双渗模型[27-28]和离散裂缝模型[29-31]等,能较为准确地描述砂岩油气藏压裂改造时储层流体的流动规律[32-35],但难以准确表征页岩气藏复杂缝网耦合多重介质系统的渗流模式,而且目前国内外尚无相关研究。为此,笔者针对页岩气吸附和扩散特征,建立了离散裂缝耦合多重连续介质系统的页岩气藏水平井缝网压裂数值模拟模型,采用局部网格加密的方法描述离散裂缝和裂缝网络,并应用多重连续介质系统描述页岩气藏微小裂缝体系。该模型充分考虑了页岩气藏多重介质分布和天然/次生裂缝发育的特点,同时结合了可以准确描述缝网的离散裂缝模型及能够精确表征流体压缩性、相态变化的多重连续介质模型。基于该模型系统分析了储层横向/纵向动用程度以及裂缝参数对页岩气藏气井产能的影响,以期为页岩气藏水平井压裂设计和产能预测提供理论依据。
1 离散裂缝耦合多重连续介质模型基于多重连续介质物理模型[25]和达西渗流公式,分别建立了裂缝和基质系统的流动方程。
裂缝系统流动方程:

|
(1) |
基质系统流动方程:
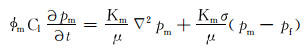
|
(2) |
式中:ϕm,ϕf分别为基质和裂缝的孔隙度;Cl为压缩系数,MPa-1;pm,pf分别为基质和裂缝的压力,MPa;μ为流体黏度,mPa·s;Km,Kf分别为基质和裂缝的渗透率,mD;σ为多重介质形状因子;t为生产时间,s。
将岩石基质和裂缝2个系统通过窜流公式联立,可得:
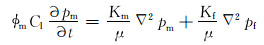
|
(3) |
与基质相比,裂缝孔隙度要小很多,因此有:
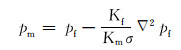
|
(4) |
可以用裂缝压力表示岩石基质压力,整理得:

|
(5) |
式(5)为裂缝中流体流动的数学模型。根据直角坐标和径向坐标的转化公式,在径向坐标下对式(5)进行了求解。
由物质守恒定律可得:

|
(6) |
式中:r为储层不同位置距井筒的距离,m。
令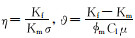
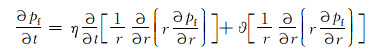
|
(7) |
采用有限差分法对式(7)进行离散,按径向划分为n个不等间距单元。井底附近不同位置处的压力变化较大,为了精确描述井底附近的压力变化特征,令井底附近的单元网格尺寸小于远井地带的网格(等比级数划分方法),则有:
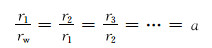
|
(8) |
由于井底附近单元网格尺寸较小,采用数值差分方法求解式(7)容易导致其不收敛。因此采用坐标变换的方法,令ln a=Δx,将不等间距的径向坐标r替换成等间距的坐标x,化简式(7)可得:
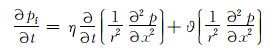
|
(9) |
式(9)为单元网格尺寸不等间距分布的离散裂缝耦合多重连续介质数学模型,采用有限差分方法对式(9)进行离散化处理,结合边界条件对差分方程进行求解。
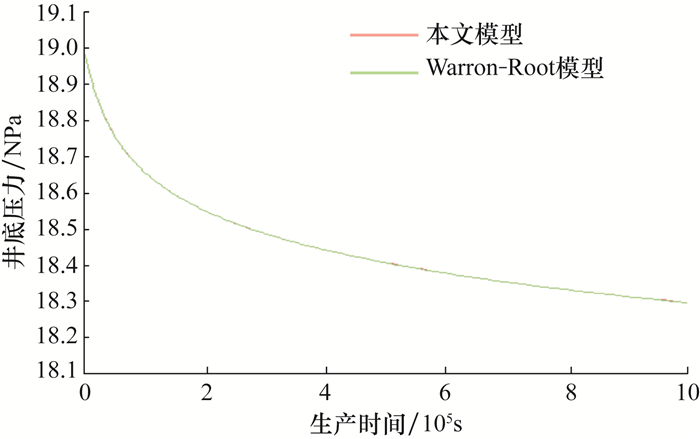
2 多重连续介质基质-裂缝网格划分目前,常采用Warron-Root双重介质模型[25]描述基质-裂缝交互渗流机制,当本文模型与双重介质模型网格剖分相同时二者描述的流体运移规律相同。采用Matlab软件对笔者建立的离散裂缝耦合多重连续介质模型(简称本文模型)及Warron-Root双重介质模型进行编程求解。图 1所示为当本文模型的网格剖分与Warron-Root双重介质模型[25]相同时生产井井底压力的变化规律。
|
| 图 1 本文模型和Warron-Root模型井底压力对比 Fig.1 Comparison on bottom hole pressures between the proposed model and Warron-Root model |
从图 1可以看出,2种模型求得的井底压力曲线基本重合,证明了模型求解及编程的准确性。基质-裂缝窜流是多重连续介质模型中的重要参数,其受形状因子的影响较大,不同的形状因子对压力分布也有影响。考虑基质团块的几何条件、裂缝间距等多个因素,常用基质团块形状因子的表达式为:
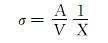
|
(10) |
式中:A为基质团块的横截面积,m2;V为基质团块的体积,m3;X为流体流动距离,m。
Warron-Root模型、Kazemi模型和Coats模型分别采用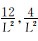


|
| 图 2 不同形状因子对井底压力的影响 Fig.2 Influence of shape factor on bottomhole pressure |
由图 2可知,形状因子越大,定产生产时井底压力越大,说明基质-裂缝窜流量就越大。
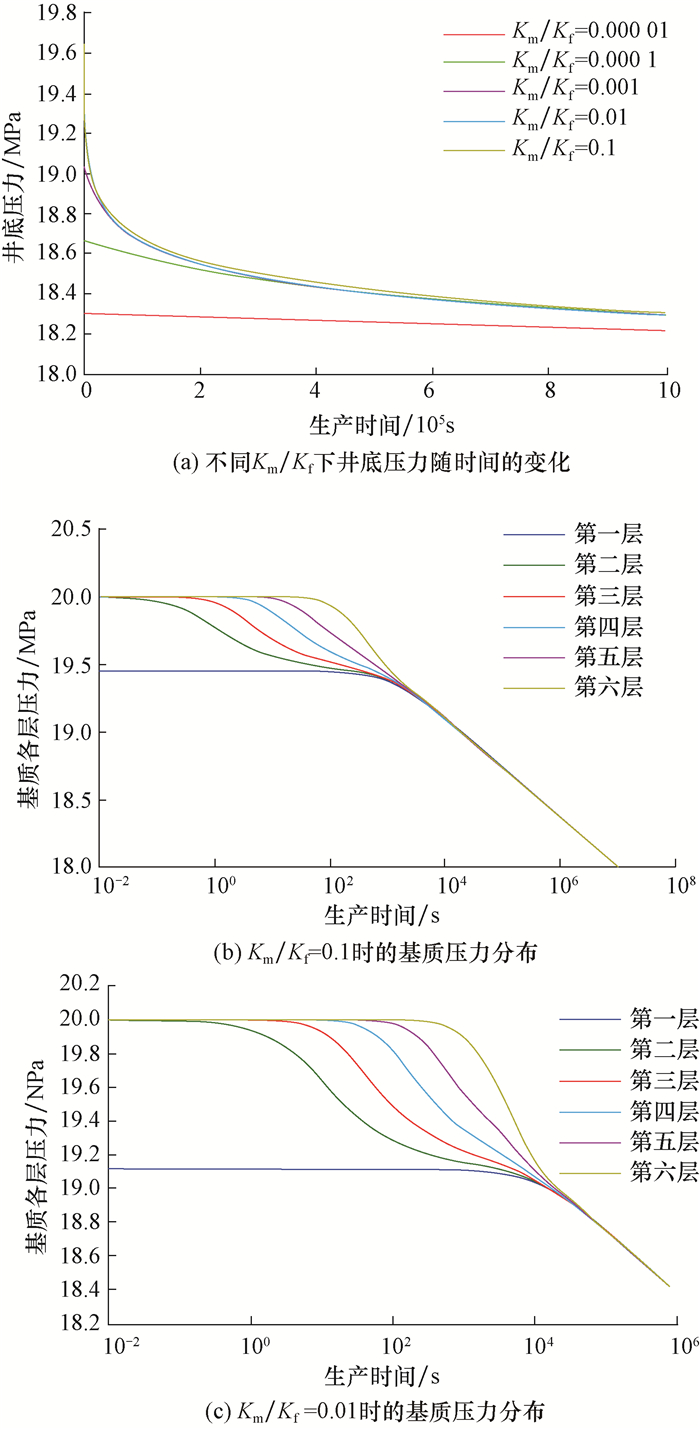
在多重连续介质系统中,采用多层嵌套方法表征基质内液体的流动规律[26]。将基质分成6层进行计算分析,取Km/Kf分别为0.000 01,0.000 1,0.001,0.01和0.1,研究不同岩石基质与裂缝渗透率比值下井底压力变化规律及多重连续介质不同层的压力分布规律,结果如图 3所示。
|
| 图 3 岩石基质与裂缝的渗透率比值对压力分布的影响规律 Fig.3 Influencing law of matrix-fracture permeability ratio on pressure distribution |
由图 3(a)可知:基质与裂缝的渗透率比值较大时,井底压力下降快,分析认为,基质渗透率与裂缝渗透率相近时流体交换流动阻力小;相反,如果基质与裂缝的渗透率比值较小,如Km/Kf=0.000 01,则井底压力下降不明显,说明流体从渗透率极低的基质中流出来较困难。由图 3(b)、图 3(c)可知:基质与裂缝的渗透率比值较大时,流体在基质内部的流动阻力较小,流动速度较快,各层压裂达到拟稳态的时间较短;反之,则流体的流动阻力较大,流动速度较慢,达到拟稳态流动的时间较长。
3 页岩气储层动用规律在深入分析页岩气藏物性参数及流动特征的基础上,基于笔者建立的离散裂缝耦合多重连续介质模型建立了考虑页岩气吸附/解吸的多重孔隙介质压裂水平井复杂缝网数值模拟模型。模拟研究单元取压裂水平井的一侧,网格数量为60×40×2,研究工区尺寸1 200 m×800 m×20 m,采用多重连续介质模型对每个网格中流体的流动规律进行表征,并以离散裂缝局部加密表征具有缝网系统复杂特征的人工主裂缝及诱导大裂缝。人工主裂缝垂直于水平井段,开启并沟通周围的天然裂缝形成诱导大裂缝,主裂缝和缝网均为天然气流通通道。同时,将诱导次裂缝与主裂缝相互交织形成的裂缝网络所包含的区域称之为储层改造体积(stimulated reservoir volume, SRV);通过调整主、次裂缝的条数和缝间距来改变缝网的动用程度,采用扩展朗缪尔等温吸附方程表征页岩气在基质中的动态吸附和解吸过程。模型参数:渗透率为0.000 1 mD,孔隙度为2%,页岩气藏深度为1 400.00 m,页岩气组分有CO2和CH4,地层温度为60 ℃,模拟气藏长度1 200.00 m,宽度800.00 m,气藏厚度20.00 m,扩散系数1.08×105 m2/d,基质-裂缝耦合系数0.08,岩石密度2 000 kg/m3,临界体积0.098 m3/(kg·mol),气藏初始压力10 MPa,模拟时间15.0年。
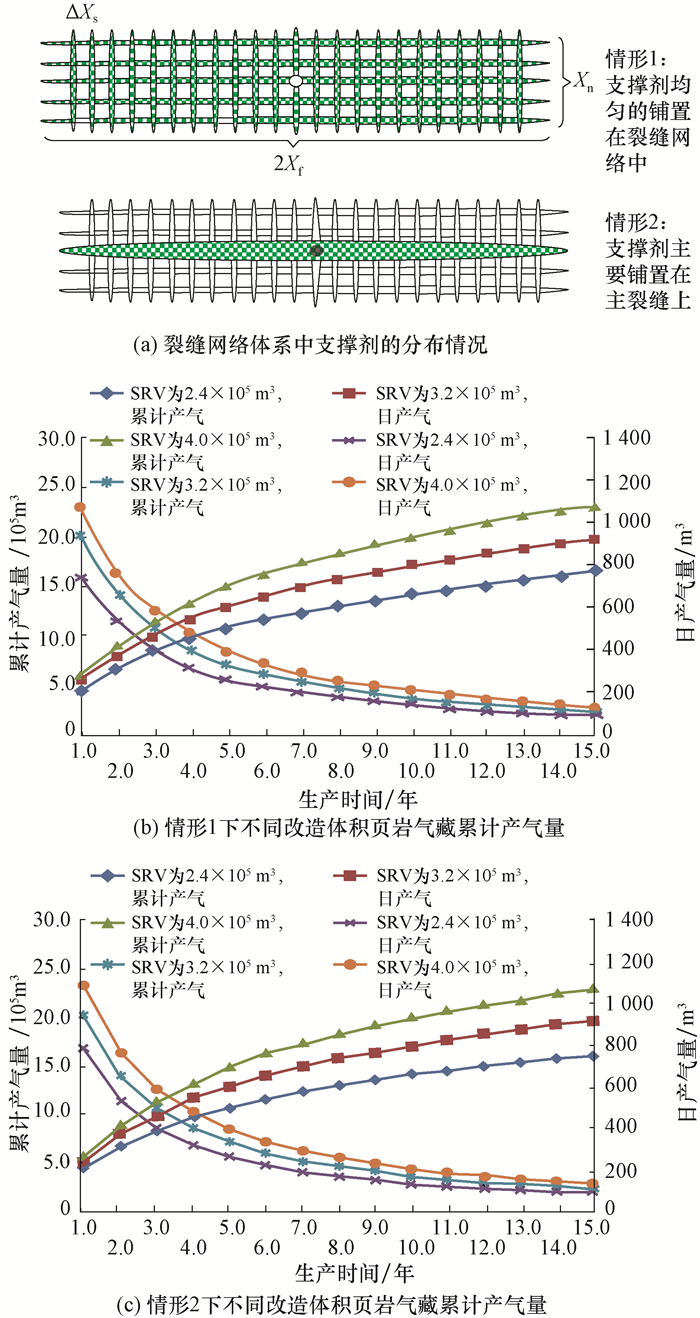
3.1 储层改造体积对页岩气产能的影响页岩气储层改造过程中,裂缝在地下的延伸情况十分复杂,支撑剂的分布对裂缝网络属性起到了决定性的作用,C.L.Cipolla等人[36]提出在压裂过程中支撑剂的2种分布规律:支撑剂平均分布到了复杂的裂缝网络中(记为情形1,其中Xf代表主裂缝缝长,Xn代表主裂缝间距,ΔXs代表次裂缝间距);支撑剂仅聚集在水力压裂的主要裂缝系统(人工裂缝),其他裂缝网络内几乎无支撑剂分布(记为情形2),如图 4所示[36]。
|
| 图 4 不同支撑剂分布时不同储层改造体积对日产气量和累计产气量影响 Fig.4 Influence of SRV on production rate and cumulative production with different proppant distributions |
当支撑剂在裂缝网络中均匀分布时,主裂缝和裂缝网络的导流能力均为0.1 D·cm;当支撑剂仅聚集在水力压裂的主缝中,主缝导流能力为1.0 D·cm,裂缝网络系统的导流能力为0.1 D·cm。通过改变裂缝间距使SRV分别为24.0×104,32.0×104和40.0×104 m3,然后应用数值模拟方法计算不同SRV条件下页岩气产量。结果表明,随着储层改造体积的增大,页岩气产气量也随之增大。支撑剂聚集方式会随着SRV的改变对页岩气的产量产生较大的影响,支撑剂均匀分布情况下累计产量较低,这表明主裂缝中支撑剂的聚集不仅对初期的产量有较大贡献,而且缝网中支撑剂的聚集会大幅度提高后期的产量,更多的页岩气解吸并流入井筒,影响最终采收率。同时,情形2的初期产气量和累计产气量都比情形1的页岩气藏压裂模型提高了10%~15%,人工主裂缝的作用不可忽略,作为直接贯通井筒与地层的主要通道,其大幅度提高了储层与井筒的连通性。
3.2 裂缝纵向动用程度对页岩气产量的影响为了评价页岩气藏裂缝网络参数对产能的影响,提出压裂水平井裂缝纵向动用程度的概念,即缝网压裂所产生的沿垂直于水平井段方向上的有效泄流(气)体积占页岩气藏储层的比值。可知,水平井裂缝纵向动用程度与水力压裂主裂缝的长度正相关,与裂缝网络中的次缝间距负相关。
运用数值模拟方法,研究了水平井裂缝纵向动用程度对页岩气产量及压力分布的影响。保证水平段长度相同,主裂缝和裂缝网络的导流能力均为0.1 D·cm,主缝半长均为100 m,间距为80 m,研究次缝间距分别为10,20和30 m时的累计产气量变化规律(见图 5(a)),并绘制了不同次裂缝间距下0.5年、1.0年以及5.0年后的储层压力分布,结果如图 5(b)所示。

|
| 图 5 不同次缝间距时页岩气藏累计产气量及压力分布规律 Fig.5 Cumulative production and pressure distribution characteristics of shale gas reservoirs under different secondary fracture spacing |
从图 5可以看出,裂缝间距越小纵向动用程度越大。储层改造区域内次裂缝连通了更多的基质储层,提高了储层纵向动用程度、增大了接触面积,流体流动效率也随之提高,泄气面积大幅增大。
3.3 裂缝横向动用程度对页岩气产量的影响裂缝横向动用程度是指缝网压裂所产生的沿平行于水平井段方向上的有效泄流(气)体积占整个页岩气藏储层的比值。裂缝横向动用程度与水平段的长度正相关,与水力压裂主裂缝间距负相关。以下分2种情况讨论主裂缝间距对产能的影响。
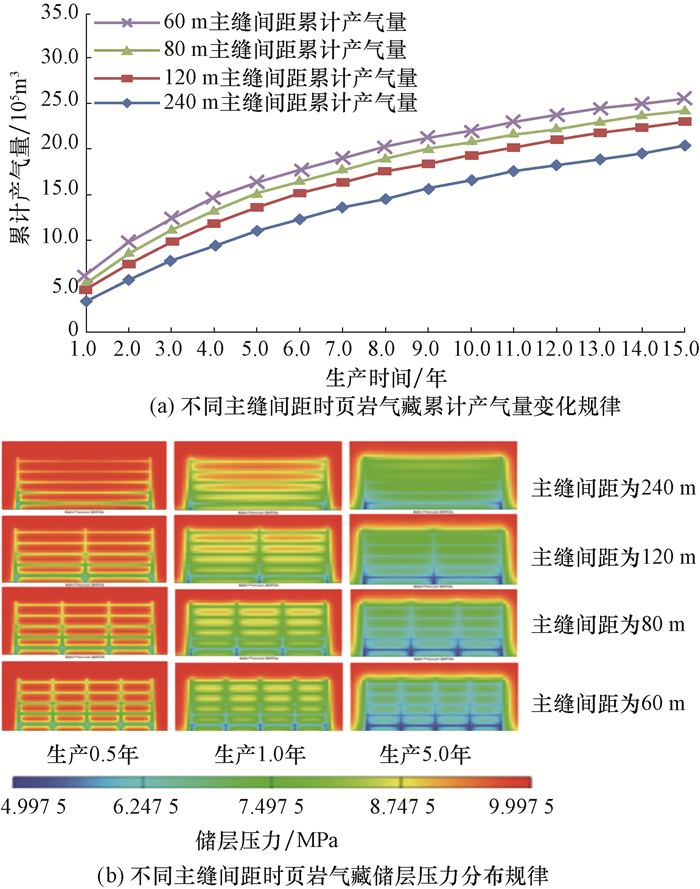
支撑剂均匀分布裂缝网络(记为情形3)。页岩气数值模拟模型主裂缝半长均为100 m,主裂缝和裂缝网络的导流能力均为0.05 D·cm,通过改变主缝间距,分析累计产气量和压力分布规律,并绘制了不同主缝间距时生产0.5,1.0和5.0年后的储层压力分布,结果如图 6所示。
|
| 图 6 不同主缝间距时页岩气藏累计产气量及压力分布特征(情形3) Fig.6 Cumulative production and pressure distribution characteristics of shale gas reservoirs under different main fracture spacing (case 3) |
由图 6可知,随着主裂缝间距减小,压裂级数增加,裂缝横向动用程度提高,页岩气产量的增加主要集中在后期;当主裂缝间距减小到120 m以后,累计产气量增加幅度变缓,分析认为,这是由于主裂缝间距变小后,裂缝之间的流动出现了干扰。
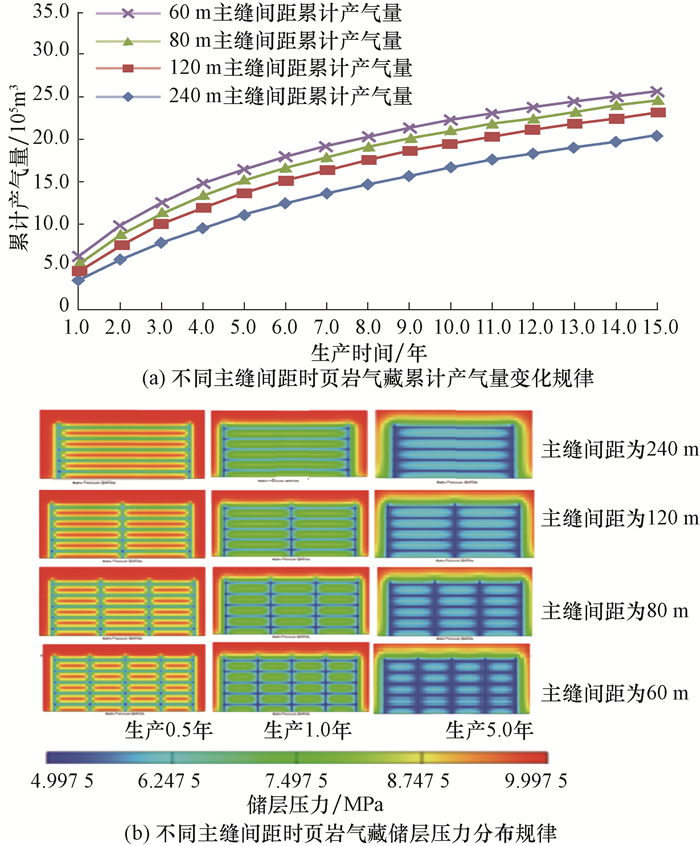
支撑剂分布在主要裂缝,裂缝网络几乎未支撑(记为情形4)。此时,裂缝网络导流能力为0.05 D·cm,主裂缝导流能力为1.0 D·cm,其他条件同。通过改变主缝间距,分析累计产气量和压力分布规律,并绘制了不同主缝间距时生产0.5, 1.0和5.0年后的储层压力分布,结果如图 7所示。
|
| 图 7 不同主缝间距时页岩气藏累计产气量及压力分布规律(情形4) Fig.7 Cumulative production and pressure distribution characteristics of shale gas reservoirs under different main fracture spacing (case 4) |
由图 7可知,随着主裂缝间距减小,相同的压裂级数也随之增加,页岩气初期产气量增加较快,后期逐渐放缓,预测15.0年后的累计产气量相近;不同方案储层改造范围内泄气范围比较有限,较大的主裂缝导流能力提高了远井地带储层的横向动用程度,能够提高单井的初期产能,随着压力波及到缝网,产量迅速达到高峰后逐渐开始下降。
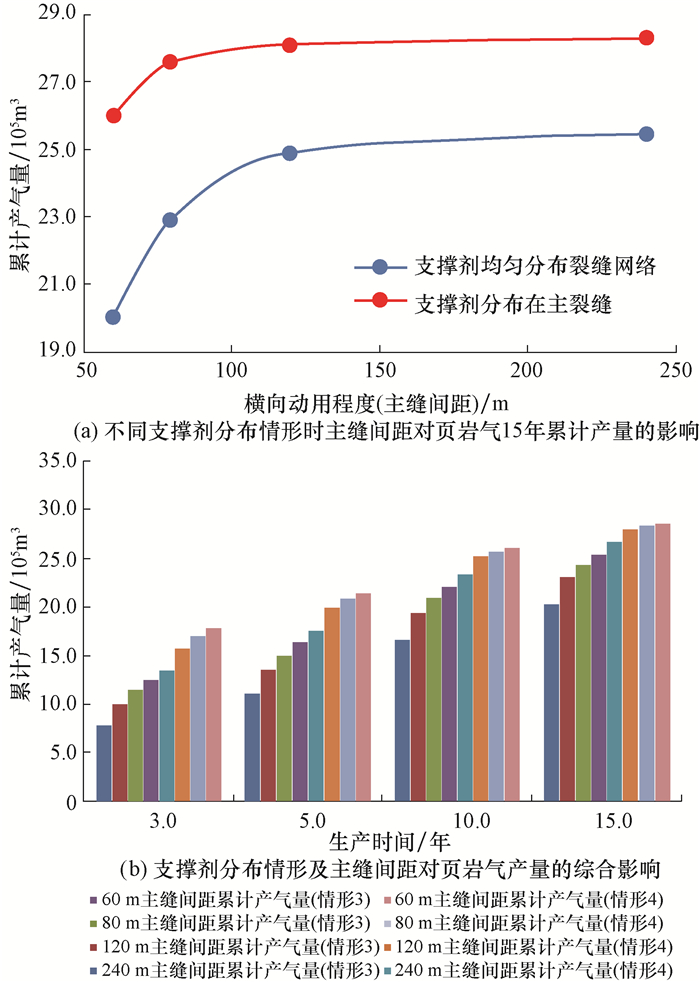
将情形3和情形4的研究数据汇总到一起进行对比分析,得到如图 8所示的结果。
|
| 图 8 不同裂缝横向动用程度时支撑剂分布情形对累计产气量的影响 Fig.8 Influence of proppant distribution on cumulative gas production under various lateral producing extents of fracture |
由图 8可知,支撑剂分布在主裂缝时累计产气量较高。具有高导流能力的主裂缝与开启的天然裂缝连通时,即使压裂级数较少时也可以获得较高的产能,同时随着压裂级数增加,与主裂缝连通的次裂缝越来越密集,缝网的整体导流能力对提高生产后期累计产气量起到了决定性作用。因此,在压裂施工过程中,应当考虑使裂缝网络和井筒之间形成更好的连通,推荐泵入低密度、高强度的支撑剂,并在压裂初期和末期泵入大粒径的支撑剂,促进主裂缝的形成,并提高主裂缝的导流能力,同时可以降低压裂的级数,大幅度降低成本。
4 结论1) 由于页岩气在基质/干酪根内部的流动阻力较大,流体流动速度极慢,达到拟稳态流动的时间较长,因此在页岩气建模过程中应选择多重连续介质模型,以准确描述页岩气的流动状态。
2) 基于多重连续介质模型耦合页岩气渗流机理,考虑人工主裂缝与复杂裂缝网络特征,建立了数值模拟模型。研究表明,页岩气开发中,当储层改造体积相同时,SRV范围内能够被连通的裂缝是贡献产量的主力,因而最大限度地开启或连通天然裂缝,增加裂缝网络与井筒及主裂缝之间的连通是提高页岩气产量的必备条件。
3) 页岩气储层改造纵向动用程度增加,气藏的压降范围更广、幅度更大,解吸气流动产出更为充分,累计产气量也越高;同样,储层横向动用程度提高,泄气效率随之增加,而较高的裂缝导流能力会加剧连通裂缝之间的相互干扰,从而影响最终开采效果。
4) 高导流能力的主裂缝是获得较高初期产能的保证,缝网的整体导流能力对提高生产后期累计产气量起到了决定性作用。压裂施工过程中应当在促进主裂缝形成的基础上,考虑提高主裂缝的导流能力,然后才是促进裂缝网络和井筒之间形成更好的连接,同时可以减少水力压裂的级数,降低开发成本。
| [1] |
KANG S M, FATHI E, AMBROSE R J, et al. Carbon dioxide storage capacity of organic-rich shales[J]. SPE Journal, 2011, 16(4): 842-855. DOI:10.2118/134583-PA |
| [2] |
YAN Bicheng, WANG Yuhe, KILLOUGH J E. Beyond dual-porosity modeling for the simulation of complex flow mechanisms in shale reservoirs[J]. Computational Geosciences, 2016, 20(1): 69-91. DOI:10.1007/s10596-015-9548-x |
| [3] |
WASAKI A, AKKUTLU I Y. Permeability of organic-rich shale[J]. SPE Journal, 2015, 20(6): 1384-1396. DOI:10.2118/170830-PA |
| [4] |
戴金星, 吴伟, 房忱琛, 等. 2000年以来中国大气田勘探开发特征[J]. 天然气工业, 2015, 35(1): 1-9. DAI Jinxing, WU Wei, FANG Chenchen, et al. Exploration and development of large gas fields in China since 2000[J]. Natural Gas Industry, 2015, 35(1): 1-9. |
| [5] |
钱斌, 张俊成, 朱炬辉, 等. 四川盆地长宁地区页岩气水平井组"拉链式"压裂实践[J]. 天然气工业, 2015, 35(1): 81-84. QIAN Bin, ZHANG Juncheng, ZHU Juhui, et al. Application of zipper fracturing of horizontal cluster wells in the Changning shale gas pilot zone, Sichuan Basin[J]. Natural Gas Industry, 2015, 35(1): 81-84. |
| [6] |
LANGE T, SAUTER M, HEITFELD M, et al. Hydraulic fracturing in unconventional gas reservoirs:risks in the geological system part 1[J]. Environmental Earth Sciences, 2013, 70(8): 3839-3853. DOI:10.1007/s12665-013-2803-3 |
| [7] |
LOUCKS R G, REED R M, RUPPEL S C, et al. Morphology, Genesis, and distribution of nanometer-scale pores in siliceous mudstones of the Mississippian Barnett Shale[J]. Journal of Sedimentary Research, 2009, 79(12): 848-861. DOI:10.2110/jsr.2009.092 |
| [8] |
YUAN Bin, SU Yuliang, MOGHANLOO R G, et al. A new analytical multi-linear solution for gas flow toward fractured horizontal wells with different fracture intensity[J]. Journal of Natural Gas Science and Engineering, 2015, 23: 227-238. DOI:10.1016/j.jngse.2015.01.045 |
| [9] |
WANG Wendong, SHAHVALI M, SU Yuliang. A semi-analytical fractal model for production from tight oil reservoirs with hydraulically fractured horizontal wells[J]. Fuel, 2015, 158: 612-618. DOI:10.1016/j.fuel.2015.06.008 |
| [10] |
WANG Wendong, SU Yuliang, SHENG Guanglong, et al. A mathematical model considering complex fractures and fractal flow for pressure transient analysis of fractured horizontal wells in unconventional oil reservoirs[J]. Journal of Natural Gas Science & Engineering, 2015, 23: 139-147. |
| [11] |
YUAN Bin, MOGHANLOO G R, SHARIFF E, et al. Integrated investigation of dynamic drainage volume (DDV) and inflow performance relationship (transient IPR) to optimize multi-stage fractured horizontal wells in shale oil[J]. Journal of Energy Resource Technology, 2016, 138(5): 052901-1-052901-9. |
| [12] |
孙海, 姚军, 孙致学, 等. 页岩气数值模拟技术进展及展望[J]. 油气地质与采收率, 2012, 19(1): 46-49. SUN Hai, YAO Jun, SUN Zhixue, et al. Recent development and prospect on numerical simulation of shale gas reservoirs[J]. Petroleum Geology and Recovery Efficiency, 2012, 19(1): 46-49. |
| [13] |
陈晓明, 李建忠, 郑民, 等. 干酪根溶解理论及其在页岩气评价中的应用探索[J]. 天然气地球科学, 2012, 23(1): 14-18. CHEN Xiaoming, LI Jianzhong, ZHENG Min, et al. Kerogen solution the oryand its exploratory applicationin shale gas assessment[J]. Natural Gas Geoscience, 2012, 23(1): 14-18. |
| [14] |
JAVADPOUR F, FISHER D, UNSWORTH M. Nanoscale gas flow in shale gas sediments[J]. Journal of Canadian Petroleum Technology, 2007, 46(10): 55-61. |
| [15] |
赵金洲, 李志强, 胡永全, 等. 考虑页岩储层微观渗流的压裂产能数值模拟[J]. 天然气工业, 2015, 35(6): 53-58. ZHAO Jinzhou, LI Zhiqiang, HU Yongquan, et al. Numerical simulation of productivity after fracturing with consideration to micro-seepage in shale reservoirs[J]. Natural Gas Industry, 2015, 35(6): 53-58. |
| [16] |
FREEMAN C M, MORIDIS G J, BLASINGAME T A. A numerical study of microscale flow behavior in tight gas and shale gas reservoir systems[J]. Transport in Porous Media, 2011, 90(1): 253-268. DOI:10.1007/s11242-011-9761-6 |
| [17] |
高树生, 于兴河, 刘华勋. 滑脱效应对页岩气井产能影响的分析[J]. 天然气工业, 2011, 31(4): 55-58. GAO Shusheng, YU Xinghe, LIU Huaxun. Impact of slippage effect on shale gas well productivity[J]. Natural Gas Industry, 2011, 31(4): 55-58. |
| [18] |
BESKOK A, KARNIADAKIS G E. A model for flows in channels, pipes, and ducts at micro and nano scales[J]. Microscale Thermophysical Engineering, 1999, 3(1): 43-77. DOI:10.1080/108939599199864 |
| [19] |
陈守雨, 刘建伟, 龚万兴, 等. 裂缝性储层缝网压裂技术研究及应用[J]. 石油钻采工艺, 2010, 32(6): 67-71. CHEN Shouyu, LIU Jianwei, GONG Wanxing, et al. Study and application on network fracturing technology in fractured reservoir[J]. Oil Drilling & Production Technology, 2010, 32(6): 67-71. |
| [20] |
王文东, 赵广渊, 苏玉亮, 等. 致密油藏体积压裂技术应用[J]. 新疆石油地质, 2013, 34(3): 345-348. WANG Wendong, ZHAO Guangyuan, SU Yuliang, et al. Application of network fracturing technology to tight oil reservoirs[J]. Xinjiang Petroleum Geology, 2013, 34(3): 345-348. |
| [21] |
雷群, 胥云, 蒋廷学, 等. 用于提高低-特低渗透油气藏改造效果的缝网压裂技术[J]. 石油学报, 2009, 30(2): 237-241. LEI Qun, XU Yun, JIANG Tingxue, et al. "Fracture network" fracturing technique for improving post-fracturing performance of low and ultra-low permeability reservoirs[J]. Acta Petrolei Sinica, 2009, 30(2): 237-241. DOI:10.7623/syxb200902013 |
| [22] |
陈作, 薛承瑾, 蒋廷学, 等. 页岩气井体积压裂技术在我国的应用建议[J]. 天然气工业, 2010, 30(10): 30-32. CHEN Zuo, XUE Chengjin, JIANG Tingxue, et al. Proposals for the application of fracturing by stimulated reservoir volume(SRV) in shale gas wells in China[J]. Natural Gas Industry, 2010, 30(10): 30-32. |
| [23] |
WITHERSPOON P A, WANG J S Y, IWAI K, et al. Validity of cubic law for fluid flow in a deformable rock fracture[J]. Water Resources Research, 1980, 16(6): 1016-1024. DOI:10.1029/WR016i006p01016 |
| [24] |
BLASKOVICH F, CAIN G M, SONIER F, et al. A multicomponent isothermal system for efficient reservoir simulation[R]. SPE 11480, 1983. https://www.osti.gov/biblio/5522592
|
| [25] |
WARREN J E, ROOT P J. The behavior of naturally fractured reservoirs[R]. SPE 426, 1963. http://www.mendeley.com/catalog/behavior-naturally-fractured-reservoirs/
|
| [26] |
LAMPE V. Modelling fluid flow and heat transport in fractured porous media[D]. Bergen: University of Bergen, 2013. http://bora.uib.no/handle/1956/7509
|
| [27] |
HILL A C, THOMAS G W. A new approach for simulating complex fractured reservoirs[R]. SPE 13537, 1985. http://dx.doi.org/10.2118/13537-MS
|
| [28] |
HO C K. Dual porosity vs. dual permeability models of matrix diffusion in fractured rock: to be submitted to the International High-Level Radioactive Waste Conference, Lus Vegas, NV, April 29-May 3, 2001[R]. http://digital.library.unt.edu/ark:/67531/metadc724039/
|
| [29] |
姚军, 王子胜, 张允, 等. 天然裂缝性油藏的离散裂缝网络数值模拟方法[J]. 石油学报, 2010, 31(2): 284-288. YAO Jun, WANG Zisheng, ZHANG Yun, et al. Numerical simulation method of discrete fracture network for naturally fractured reservoirs[J]. Acta Petrolei Sinica, 2010, 31(2): 284-288. DOI:10.7623/syxb201002018 |
| [30] |
NOORISHAD J, MCHRAN M. An upstream finite element method for solution of transport equation in fractured porous media[J]. Water Resources Research, 1982, 18(3): 588-596. DOI:10.1029/WR018i003p00588 |
| [31] |
BACA R G, ARNETT R C, LANGFORD D W. Modeling fluid-flow in fractured porous rock masses by finite-element techniques[J]. International Journal for Numerical Methods in Fluids, 1984, 4(4): 337-348. DOI:10.1002/(ISSN)1097-0363 |
| [32] |
CARLSON E S, MERCER J C. Devonian shale gas production:mechanisms and simple models[J]. Journal of Petroleum Technology, 1991, 43(4): 476-482. DOI:10.2118/19311-PA |
| [33] |
DINGA D Y, WU Y S, JEANNIN L. Efficient simulation of hydraulic fractured wells in unconventionalreservoirs[J]. Journal of Petroleum Science and Engineering, 2014, 122: 631-642. DOI:10.1016/j.petrol.2014.09.005 |
| [34] |
WANG Cong, WU Yushu. Modeling analysis of transient pressure and flow behavior at horizontal wells with multi-stage hydraulic fractures in shale gas reservoirs[R]. SPE 168966, 2014. http://dx.doi.org/10.2118/168966-MS
|
| [35] |
JIANG Jiamin, SHAO Yuanyuan, YOUNIS R M. Development of a multi-continuum multi-component model for enhanced gas recovery and CO2 storage in fractured shale gas reservoirs[R]. SPE 169114, 2014.
|
| [36] |
CIPOLLA C L, LOLON E, MAYERHOFER M J. Reservoir modeling and production evaluation in shale-gas reservoirs[R]. IPTC 13185, 2009. http://dx.doi.org/10.2523/IPTC-13185-MS
|


