2. 中国石油大学(华东)石油工程学院, 山东青岛 266580
2. School of Petroleum Engineering, China University of Petroleum(Huadong), Qingdao, Shandong, 266580, China
磁力随钻测斜仪是井眼轨迹控制中最常用的测量仪器,主要用于测量井斜角、方位角等井眼轨迹参数, 其测量精度除了与仪器自身的质量有关外,还与地磁场有直接关系[1-2]。钻柱磁化等因素引起的轴向磁干扰会导致磁力随钻测斜仪测量的方位角不准确[3-4],容易造成脱靶、井眼交碰等问题。针对该问题,M.K.Russell等人[5]提出了一种较为准确的间接校正方法,徐涛、罗武胜等人[6-7]对该方法进行了介绍与分析;Sperry-Sun公司[8]的随钻测量软件提供了一种间接校正方法, 即短钻铤测量修正法。笔者分析了Russell法和短钻铤测量修正法这2种间接校正方法的原理及计算过程,针对其存在的计算过程较为复杂的问题,提出了矢量和法和钻具截面法2种直接校正方法;采用数据仿真方法分析了轴向干扰磁场对方位角的影响,对比了4种校正方法的准确性,评价了其应用效果。
1 磁力随钻测斜仪测量原理目前,磁力随钻测斜仪主要是通过安装在探管内部的3个相互垂直的重力加速度计和3个相互垂直的磁通门传感器测量每个方向上的重力分量和地磁场分量,然后根据测得的分量来计算井斜角、方位角和工具面角等参数。在测量过程中,地磁场分量最容易受到干扰,当地磁场受到干扰时,磁感应强度及磁倾角都可能发生变化,导致测量的地磁场分量不准确,进而导致计算的方位角存在偏差[9-10]。
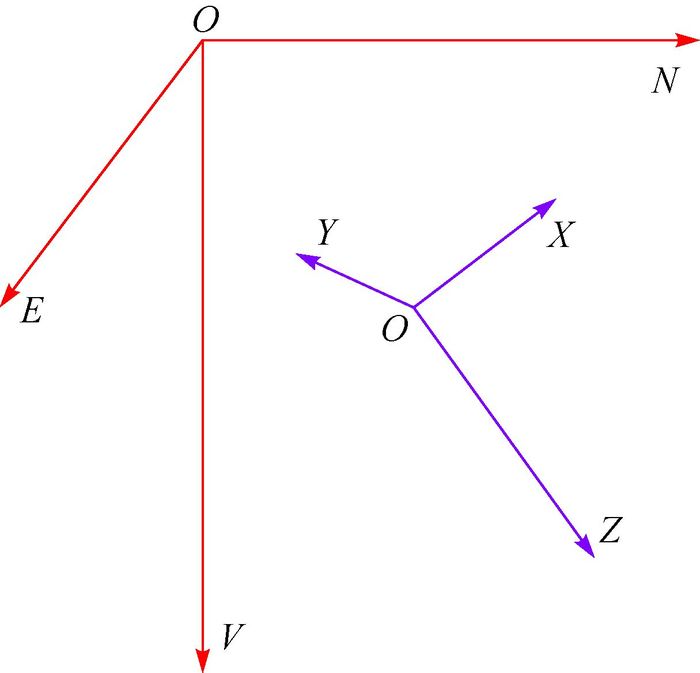
为了便于说明,以井口为原点O,建立大地坐标系NEV,仪器坐标系为XYZ(见图 1)。其中OZ沿探管轴向方向指向探管下部,X轴、Y轴在仪器横截面上,X轴与螺杆弯曲方向一致。重力加速度计和磁通门传感器分布在XYZ坐标系的3个轴上。
|
| 图 1 大地坐标系与仪器坐标系 Fig.1 Geodetic coordinate system and instrument coordinate system |
仪器坐标系通过井斜角、方位角和工具面角等参数可以转换到大地坐标系,利用这种关系可得:
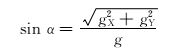
|
(1) |
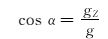
|
(2) |
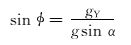
|
(3) |
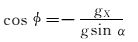
|
(4) |
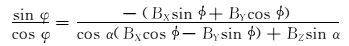
|
(5) |
式中:α为井斜角,(°);φ为方位角,(°);φ为高边工具面角,(°);g为重力加速度,m/s2;gX、gY、gZ为重力加速度分量,m/s2;BX、BY和BZ为地磁场磁感应强度分量[3-4],μT。
实际钻井过程中,为了防止磁力随钻测斜仪受到干扰,一般将其放置在无磁钻铤内,但由于无磁钻铤前后端仍为磁性钻具,会产生附加的干扰磁场,如果无磁钻铤的长度不够,或是无磁钻铤被磁化,都会导致地磁场磁感应强度分量测量不准确,使计算得到的方位角偏差较大,进而影响井眼轨迹控制精度。
2 轴向磁干扰的间接校正方法轴向磁干扰校正的前提是磁力随钻测斜仪径向磁通门传感器测得的地磁场磁感应强度分量BX、BY是准确的,而影响仪器的干扰磁场是沿钻具轴线方向。无磁钻铤前后的钻铤或钻杆不仅轴线对称,而且相对钻具轴线上的仪器测点较远,故其造成的干扰磁场为钻具轴线方向。M.K.Russell等人[5, 11]研究发现,当无磁钻铤长度大于3.05 m时,钻具磁化产生的径向磁干扰可以忽略不计。目前,国外主要有短钻铤测量修正法和Russell法2种间接轴向磁干扰校正方法,计算过程中需要进行循环迭代。
2.1 短钻铤测量修正法Sperry-Sun公司的随钻测量软件提供了一种短钻铤测量修正方法[8, 12],是采用循环迭代的方法来间接校正方位角。其基本原理是:在没有磁干扰的情况下,井斜角、方位角可以通过3个重力加速度分量和3个磁感应强度分量之间的关系计算得到,同时也可以利用这种关系来反求轴向磁感应强度分量BZC,然后再利用计算得到的轴向磁感应强度分量求解方位角, 其基本计算公式为:
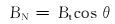
|
(6) |
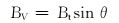
|
(7) |
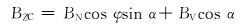
|
(8) |

|
(9) |
式中:BN为地磁场的水平分量,μT;BV为地磁场的垂向分量,μT;θ为磁倾角,(°);Bt为地磁场磁感应强度,μT;BZC为轴向磁感应强度分量,μT。
当存在轴向磁干扰时,式(8) 和式(9) 中的BZC、φ都是不准确值,需要迭代求解,具体求解过程为:
1) 利用初始测量得到的重力加速度分量和磁感应强度分量求解得到初始方位角φ,然后依据真实地磁场磁感应强度、磁倾角等参数,利用式(6)—式(8) 计算出BZC;
2) 将计算得到的BZC代入式(9) 中,可以计算出新的方位角φ,然后将新方位角φ代入式(8) 中计算出新的BZC;
3) 设置精度值ε,如果当前求解出来的φ与上次循环得出的φ相差小于ε,循环结束;如果大于ε,继续进行循环求解。
2.2 Russell法该方法是由M.K.Russell等人提出,它是根据真实地磁场、轴向干扰磁场和实测磁场之间的几何关系及物理意义得出的[5],其特征在于循环递推,逐次逼近,收敛于真实方位角[13-15]。真实地磁场、轴向干扰磁场和实测磁场分别用B、e和Bm表示,三者之间关系为e=Bm-B,其关系如图 2所示。

|
| 图 2 轴向磁干扰的影响关系 Fig.2 Influence of axial magnetic interference |
由于受到轴向干扰磁场e的影响,导致原始地磁场磁力线发生改变,而原始磁力线在水平面上的投影是磁北方向N,受影响后磁力线在水平面上的投影已不在是磁北方向,而是图 2中的BNm,它们之间的角度差为φe。磁力随钻测斜仪测量计算得到的方位角是井眼轴线与原始地磁线在水平面投影(真磁北)之间的夹角,记为φ;受磁干扰后,得到的方位角是井眼轴线与受磁干扰后的磁力线在水平面投影之间的夹角,记为φm。
由于轴向干扰磁场是固定的,在理论上φe与φ都是稳定的唯一值。而在实际测量过程中这2个参数都是未知数,所以需要根据上述原理及相互之间的物理关系寻找φe与φ之间的联系,然后求解。
由图 2所示的几何关系可知,轴向干扰磁场e可表示为:

|
(10) |
式中:UN、UE、UV分别为北、东、垂向上的单位矢量。
由于干扰磁场e沿井眼轴线方向,所以还可以用真实方位角φ和井斜角α来表示干扰磁场:
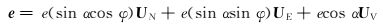
|
(11) |
式中:e为干扰磁场e的模量,μT。
由式(10) 和式(11),可得:
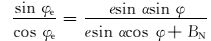
|
(12) |
由于干扰磁场e沿井眼轴线方向,即仪器坐标系中的Z轴方向,所以e可以表示为:

|
(13) |
式中:BZm是仪器实测的Z轴方向磁感应强度分量,μT;BZ是不存在干扰情况下Z轴方向磁感应强度分量,μT。
最终, 式(12) 可以表示为:
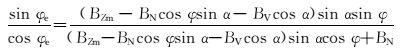
|
(14) |
式(14) 中存在未知数φ和φe,采用循环迭代的方法求得φ,具体计算过程为:
1) 用初始测量得到的φm代替φ代入式(14) 中,求出φe,然后根据φ=φm+φe,求出φ;
2) 将步骤1) 求得的φ代入到式(14) 中,求解出一个新的φe,然后得出新的φ;
3) 设置精度值ε,如果当前步求解出来的φ与上次循环得出的φ的差小于ε时,循环结束;如果大于ε,继续进行循环求解,直至求得的φ与上次循环得出的φ的差小于ε。
3 轴向磁干扰的直接校正方法Russell法和短钻铤测量修正法2种间接校正方法均需要进行循环迭代,计算过程较为复杂,为此笔者提出了矢量和法及钻具截面法这2种计算简单的直接校正方法。
3.1 矢量和法磁力随钻测斜仪测量的3个磁感应强度分量的矢量和就是地磁场,所以矢量和法磁干扰校正方法是利用已知的地磁场磁感应强度Bt及测量得到的准确的径向磁感应强度分量BX和BY来计算轴向磁感应强度分量BZC,然后利用BZC来求解真实方位角。基本计算公式为:
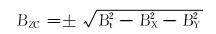
|
(15) |
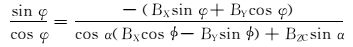
|
(16) |
式中:Bt为地磁场磁感应强度,μT。
首先根据式(15) 求得BZC,然后利用式(16) 得到真实方位角。在实际钻井过程中,如果由于更换钻具组合导致方位角测量不准确,但能够确保已钻井眼轨迹的地磁场磁感应强度、方位角等参数的准确性,可以选择这种校正方法。
这种方法虽然简单,但在计算BZC时会出现2个值,也就会得到2个方位角,这时需要根据已钻井眼轨迹的方位角进行判断,依次选择与上一测点方位角接近的方位角为正确值。在实际钻井过程中,相邻测点的方位角和井斜角不会相差太大,所以选择接近的方位角为真实方位角是合理的。
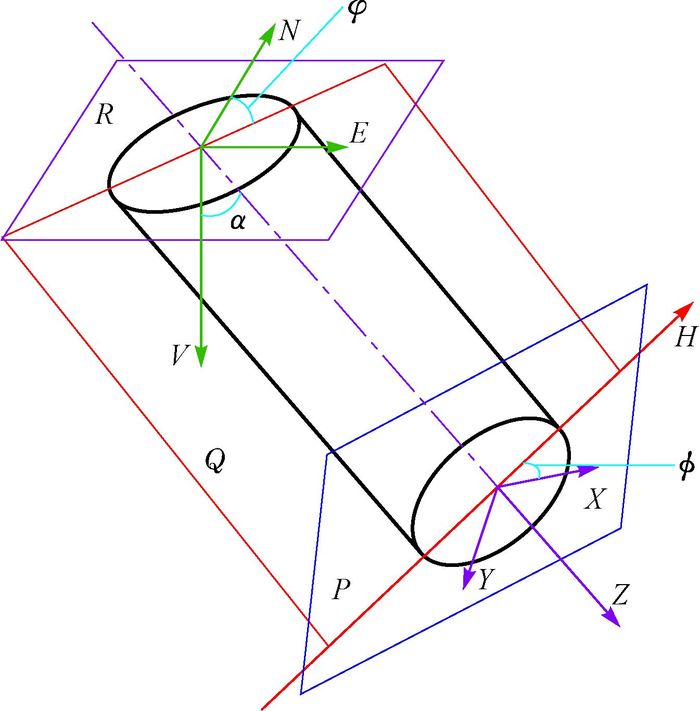
3.2 钻具截面法钻具截面法是利用当地磁场参数和测量得到的准确的径向磁感应强度分量,通过方位角建立它们之间的几何关系,然后反求方位角。为了便于说明,建立大地坐标系NEV和仪器坐标系XYZ(见图 3),Z轴沿钻柱轴线方向,X轴与Y轴沿钻柱径向方向;H方向为井眼高边方向线,R为水平面,Q为钻具(井眼)弯曲铅锤面,P为钻具(井眼)横截面。
|
| 图 3 大地坐标系与仪器坐标系 Fig.3 Geodetic coordinate system and instrument coordinate system |
由于受到轴向磁干扰的影响,导致BZ不准确,所以为了排除BZ的影响,在P平面内,将径向磁感应强度分量与磁感应强度向井眼高边方向H和与之垂直的水平方向分解,建立方程组:
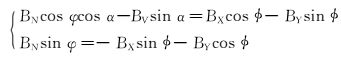
|
(17) |
式(17) 中的BN、BV由式(6)、式(7) 得到。由式(17) 可以得到:
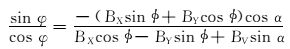
|
(18) |
利用地磁场的垂向分量BV与径向磁感应强度分量BX、BY,根据式(18) 可以得到真实方位角φ。但从式(18) 可以看出,当井斜角为90°时,由于cos α=0,所以将无法得到正确的方位角。
4 轴向磁干扰的校正仿真对上述4种磁干扰校正方法编写计算机程序,构造仿真数据来模拟轴向磁干扰及其校正过程。已知ε=0.001°,地磁场磁感应强度B=53.0μT,磁倾角为55°。
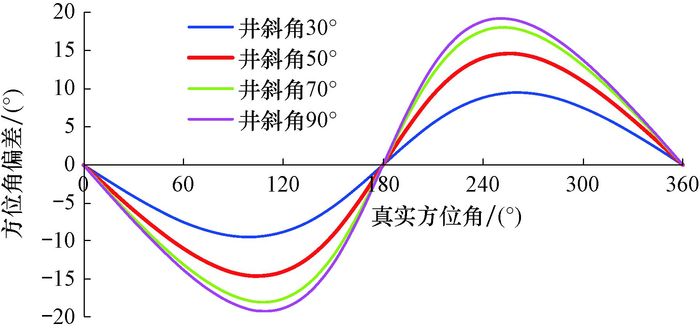
取轴向干扰磁场e=10.0μT,计算不同井斜角、真实方位角时的方位角偏差(指实测方位角与真实方位角之差),结果如图 4所示。
|
| 图 4 方位角偏差随井斜角、方位角变化的规律 Fig.4 The variation laws of azimuth deviation with the inclination and azimuth |
从图 4可以看出,在干扰磁场固定的情况下,方位角偏差随着井斜角增大而增大。在井斜角一定、真实方位角为0°~180°时,方位角偏差为负值,即实测方位角小于真实方位角,方位角偏差的绝对值先增大后减小,在真实方位角为110°左右时,达到最大值;真实方位角为180°~360°时,方位角偏差为正值,即实测方位角大于真实方位角,方位角偏差先增大后减小,真实方位角为250°左右时,达到最大值。
假设真实井斜角为50°和90°,真实方位角为70°和230°,重力工具面角为30°,轴向干扰磁场为e=5.0 μT,利用上述4种磁干扰校正方法进行校正计算,结果如表 1所示。
| 井斜角/(°) | 真实方位角/(°) | BX/μT | BY/μT | 校正方位角/(°) | ||||
| 矢量和法 | 钻具截面法 | 短钻铤法 | Russell法 | |||||
| 50 | 70 | -37.297 | -11.452 | 70 | 147.34 | 70 | 70 | 70 |
| 50 | 230 | -28.036 | 43.077 | 230 | 210.61 | 230 | 230 | 230 |
| 90 | 70 | -51.882 | -3.032 | 70 | 110 | 86.72 | 69.92 | 69.94 |
| 90 | 230 | -25.955 | 41.875 | 310 | 230 | 209.57 | 230.02 | 230.02 |
从表 1可以看出,矢量和法会得到2个方位角值,如果能够判断哪个是正确值,其校正结果是比较准确的;在井斜角为90°时,钻具截面法无法得到正确的方位角;对于上述各种情况,2种间接校正方法的计算结果均较为准确。
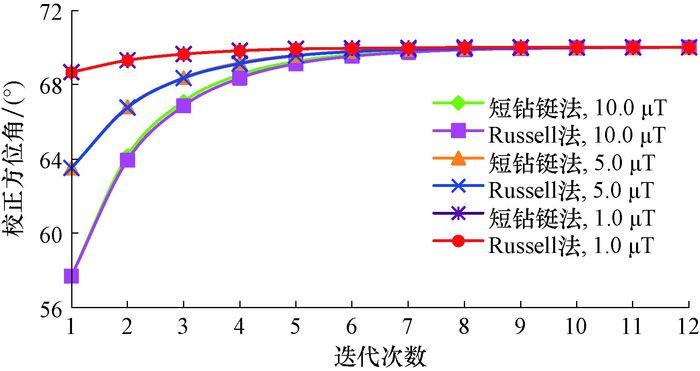
假设井斜角为50°,方位角为70°,重力工具面角为30°,当轴向干扰磁场分别取e1=1.0 μT、e2=5.0 μT、e3=10.0 μT时,应用Russell法和短钻铤测量修正法对不同轴向磁干扰情况下的方位角进行了校正,迭代计算结果见图 5。由图 5可以看出,随着轴向磁干扰增强,实测方位角的偏差增大,迭代次数增多,但经过迭代计算后的方位角都收敛于真实方位角,表明这2种间接校正方法都具有较好的稳定性和准确性。
|
| 图 5 不同轴向磁干扰下方位角校正的迭代计算结果 Fig.5 Iterative calculation of azimuth correction under different axial magnetic interferences |
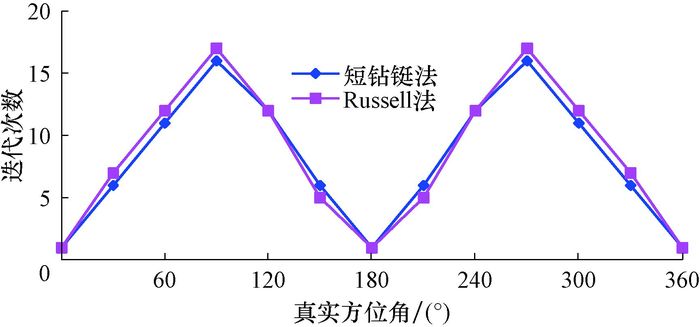
假设井斜角为50°和90°,工具面角为30°,轴向干扰磁场e=5.0 μT,ε=0.001°,应用Russell法和短钻铤测量修正法对方位角进行校正时,迭代次数与真实方位角的关系曲线如图 6和图 7所示。
|
| 图 6 井斜角50°时真实方位角与迭代次数的关系 Fig.6 Relationship between true azimuth and iteration number for 50°inclination |
|
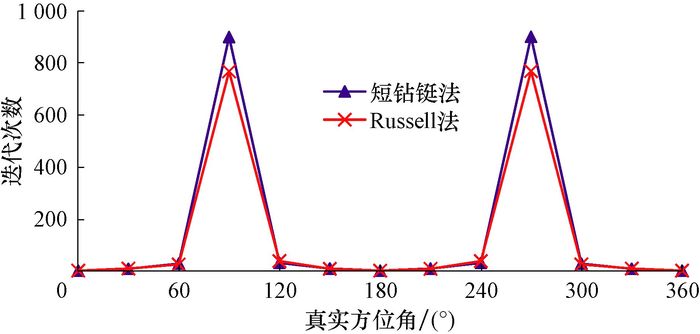
| 图 7 井斜角90°时时真实方位角与迭代次数的关系 Fig.7 Relationship between true azimuth and iteration number for 90°inclination |
由图 6和图 7可以看出,在同一井斜角条件下,真实方位角为90°和270°时,达到精度要求所需的迭代次数最多;真实方位角为0°和180°时,迭代次数最少,为1次。由图 7可以看出,当井斜角为90°,真实方位角为90°和270°时,所需迭代次数多达近1 000次,明显多于其他情况,而且计算结果显示,应用Russell法校正后的方位角分别为89.16°和270.84°,应用短钻铤测量修正法校正后的方位角分别为88.13°和271.87°,校正效果最差。由此可以看出,在这种情况下,无论从迭代次数还是最终的迭代结果来看,Russell法比短钻铤测量修正法的准确性更高。分析认为,短钻铤测量修正法是直接迭代求取方位角的正切值,并且式(9) 中分母为0或者很小,导致迭代次数多、校正效果差;而Russell法是迭代求取方位偏差角的正切值,并且式(14) 中分母约为BN,所以校正效果相对较好。但是在其他情况下,这2种校正方法的校正结果基本一致(见图 5—图 7)。
5 结论与建议1) 轴向磁干扰的4种校正方法各具特点,现场施工过程中,在无磁钻具长度不够或被磁化等情况下,可以根据不同的情况选择不同的校正方法。
2) 井眼轨迹接近水平东西方向时,轴向磁干扰的校正效果最差,所需迭代次数最多。
3) 在不影响径向磁感应强度测量的前提下,可以利用校正方法,减少无磁钻具的使用长度,缩短仪器测点至钻头的距离,降低井斜角等参数的预测难度。
4) 轴向磁干扰校正的前提是随钻测斜仪径向不存在磁干扰,但目前对径向磁干扰的研究较少,建议进一步开展径向磁干扰校正的研究工作。
| [1] |
石在虹, 滕少臣, 刘子恒.
国际地磁参考场解算方法及石油工程应用[J]. 石油钻采工艺, 2016, 38(4): 409–414.
SHI Zaihong, TENG Shaochen, LIU Ziheng. Algorithm for international geomagnetic reference field and its application in petroleum engineering[J]. Oil Drilling & Production Technology, 2016, 38(4): 409–414. |
| [2] |
曹向峰, 管志川, 王智锋, 等.
煤层气连通井导向钻井钻头定位方法[J]. 石油钻采工艺, 2016, 38(2): 151–155.
CAO Xiangfeng, GUAN Zhichuan, WANG Zhifeng, et al. Drill bit positioning method based on connected well guidance for coalbed methane[J]. Oil Drilling & Production Technology, 2016, 38(2): 151–155. |
| [3] |
乔传尚.
YST-48R型MWD仪器的Bt值异常分析与判断[J]. 石油仪器, 2011, 25(4): 23–25.
QIAO Chuanshang. Measurement and analysis of abnormal Bt value of YST-48R MWD[J]. Petroleum Instruments, 2011, 25(4): 23–25. |
| [4] |
梁奇敏, 何俊才, 董文涛, 等.
"井工厂"作业时直井段防碰设计与控制探讨[J]. 石油钻采工艺, 2016, 38(3): 302–306.
LIANG Qimin, HE Juncai, DONG Wentao, et al. Anti-collision design and control of vertical section in 'well plant' mode[J]. Oil Drilling & Production Technology, 2016, 38(3): 302–306. |
| [5] | RUSSELL M K, RUSSELL A W.Surveying of borehole:US 4163324[P].1979-08-07. |
| [6] |
罗武胜, 徐涛, 杜列波.
基于加速度计和磁强计的定向钻进姿态测量及方位校正[J]. 国防科技大学学报, 2007, 29(1): 106–110.
LUO Wusheng, XU Tao, DU Liebo. Directional drilling attitude measurement and azimuth correction with accelerometers and magnetometers[J]. Journal of National University of Defense Technology, 2007, 29(1): 106–110. |
| [7] |
徐涛, 温东, 孙晓磊.
基于加速度计和磁强计的方位测量与校正技术研究[J]. 仪器仪表学报, 2009, 30(10): 2018–2022.
XU Tao, WEN Dong, SUN Xiaolei. Research on azimuth measurement and correction technique with accelerometer and magnetometer[J]. Chinese Journal of Scientific Instrument, 2009, 30(10): 2018–2022. |
| [8] | Sperry-Sun Drilling Services Company.Basic concepts of directional surveying[R].1995. |
| [9] |
张苏, 管志川, 王建云, 等.
邻井套管对井斜方位角的影响[J]. 石油钻探技术, 2013, 41(6): 51–55.
ZHANG Su, GUAN Zhichuan, WANG Jianyun, et al. Impact of casing on adjacent well azimuth[J]. Petroleum Drilling Techniques, 2013, 41(6): 51–55. |
| [10] |
高德利, 刁斌斌.
复杂结构井磁导向钻井技术进展[J]. 石油钻探技术, 2016, 44(5): 1–9.
GAO Deli, DIAO Binbin. Development of the magnetic guidance drilling technique in complex well engineering[J]. Petroleum Drilling Techniques, 2016, 44(5): 1–9. |
| [11] |
许昊东, 黄根炉, 张然, 等.
磁力随钻测量磁干扰校正方法研究[J]. 石油钻探技术, 2014, 42(2): 102–106.
XU Haodong, HUANG Genlu, ZHANG Ran, et al. Method of magnetic interference correction in survey with magnetic MWD[J]. Petroleum Drilling Techniques, 2014, 42(2): 102–106. |
| [12] |
王明哲, 陆斌, 于跃军.
Sperry-Sun MWD轴向磁干扰的解决方法及应用[J]. 石油仪器, 2008, 22(2): 47–49.
WANG Mingzhe, LU Bin, YU Yuejun. Solution to the axial magnetic interference on Sperry-Sun MWD[J]. Petroleum Instruments, 2008, 22(2): 47–49. |
| [13] | van DONGEN J C M, MAEKIAHO L B.Method for determining the azimuth of a borehole:US 4682421[P].1987-07-28. |
| [14] |
王锐, 崔朋波, 刘培军.
MWD独立误差源的确定分析[J]. 特种油气藏, 2011, 18(5): 120–123.
WANG Rui, CUI Pengbo, LIU Peijun. Determinative analysis of MWD independent error sources[J]. Special Oil & Gas Reservoirs, 2011, 18(5): 120–123. |
| [15] |
李翠, 高德利, 刘庆龙, 等.
邻井随钻电磁测距防碰计算方法研究[J]. 石油钻探技术, 2016, 44(5): 52–59.
LI Cui, GAO Deli, LIU Qinglong, et al. A method of calculating of avoiding collisions with adjacent wells using electromagnetic ranging surveying while drilling tools[J]. Petroleum Drilling Techniques, 2016, 44(5): 52–59. |




