2. 页岩油气富集机理与有效开发国家重点实验室, 北京 100101;
3. 油气藏地质及开发工程国家重点实验室(西南石油大学), 四川成都 610500
2. State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and Effective Development, Beijing, 100101, China;
3. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan, 610500, China
井漏是油气钻井中最常见的井下复杂情况之一[1],严重威胁着钻井安全和效率[2-4]。当前,通常的做法是根据裂缝宽度确定防漏堵漏液配方及施工工艺[5-6]。一般采用以下2种方法估算井下裂缝宽度:一是根据漏失速率依据经验判断裂缝宽度;二是根据漏失速率曲线反演裂缝宽度[7]。第一种方法简单,但可靠性差,往往需要多次调整配方才能达到理想的防漏堵漏效果;第二种方法较为科学,但是其应用效果与漏失模型紧密相关。
20世纪90年代中期,O.Lietard和F.Sanfillippo等人[8-9]分别建立了宾汉流体和牛顿流体漏失模型。其后,国内外学者对漏失模型不断完善,形成了考虑裂缝变形、壁面滤失和非牛顿流体的一维线性与二维平面裂缝漏失模型[10-11],但是上述研究均未考虑裂缝粗糙度的影响。由于天然裂缝表面是粗糙的,为了深入研究粗糙度的影响,A.Lavrov和M.Ozdemirtas等人[12-13]假设钻井液是牛顿流体,进行了数值模拟和室内试验。但钻井液并非牛顿流体,采用牛顿流体研究得出的规律有待验证。贾利春等人[14]在模型中引入裂缝迂曲度表征裂缝面粗糙度的影响,但裂缝迂曲度与粗糙度不同,不能完全反映粗糙度的影响。针对上述问题,笔者基于分形理论构建了粗糙裂缝,利用赫-巴模式描述钻井液的非牛顿流体特性,并考虑裂缝非线性变形对漏失的影响,采用中点差分方法对漏失模型进行数值求解,研究了裂缝粗糙度对钻井液漏失的影响。
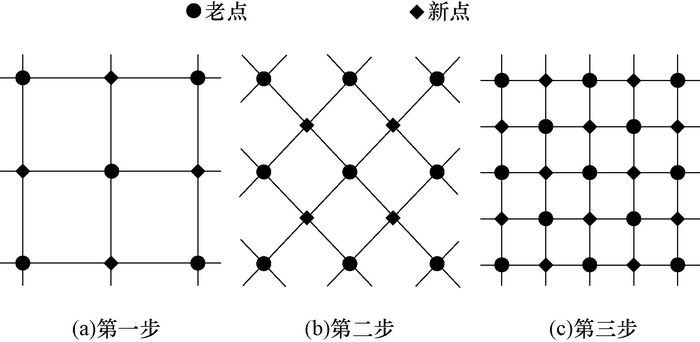
1 粗糙裂缝的表征大量研究表明,天然裂缝面是粗糙的,具有很好的自相似性,可采用分形理论进行研究。分形理论中常采用分形维数D和Hurst指数H表征裂缝表面的粗糙度,通常H=3-D[15]。光滑裂缝面是2维,极端粗糙裂缝面接近3维,实际裂缝面为2~3维。计算机生成粗糙裂缝面的方法有多种,如中点位移法、逐次随机累加法、随机布朗函数法、调整法和样条函数法[16],其中,中点位移法和逐次随机累加法较为常用[17]。中点位移法的基本原理为(如图 1所示):1) 生成矩形4个角点的缝宽值,一般取均值为0、方差为σ2的高斯随机变量;2) 生成中心点的缝宽值,取4个角点宽度的平均值加上一个均值为0、方差为σ2的高斯随机变量;3) 生成4个边中心点的缝宽值,取各边端点与中心点缝宽的平均值加上一个均值为0、方差为σ2的高斯随机变量;4) 重复步骤2) 和3),使网格数增加,一般递归4次就可以得到具有分形特征的粗糙裂缝面。
|
| 图 1 用中点位移法生成的二维粗糙裂缝面 Fig.1 Two dimensional rough fracture surfaces generated through the midpoint displacement method |
生成粗糙裂缝面后,再采用M.Ozdemirtas等人[13]的研究方法,选择一个基准面,通过调整粗糙裂缝面与基准面的位置(预设缝宽)来表征粗糙裂缝的缝宽分布。裂缝宽度可表示为:
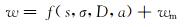
|
(1) |
式中:w为裂缝宽度,mm;f为裂缝面生成算法;s为网格尺寸;σ为标准差,mm;a为种子数;wm为预设缝宽,mm。
网格尺寸反映了网格数的多少,网格尺寸越小,网格数也越多;标准差反映了随机生成裂缝的宽度偏离平均值的程度,标准差越大,数据离散程度越高。由于计算机生成的随机数是通过一定数学方法得到的伪随机数,种子数是这个序列伪随机数的第一个数,种子数不同,生成的伪随机数序列不同。因此,网格尺寸、标准差、分形维数和种子数均影响生成裂缝的粗糙程度。种子数可以取任意值,相同分形维数、不同种子数所产生裂缝的形态不同,漏失速率及漏失量也不同,不存在规律性,故笔者未对种子数的影响进行数值模拟。
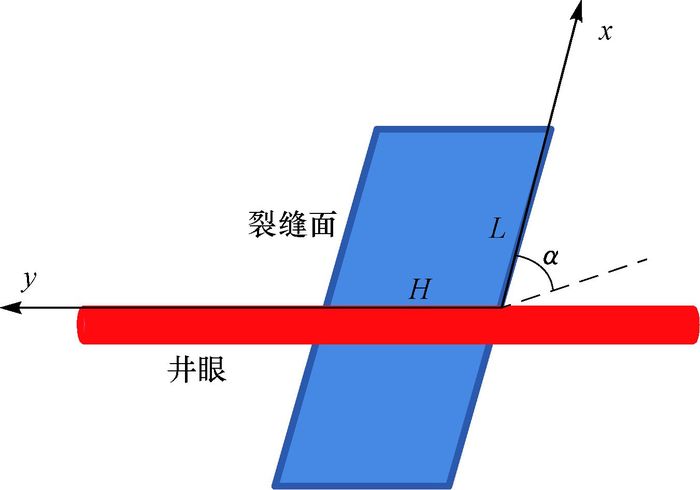
2 钻井液漏失模型 2.1 基本假设假设为水平井眼,地层中存在一条矩形粗糙裂缝,井眼中轴线恰好通过裂缝面,把1条裂缝分为2个大小不同的矩形裂缝,如图 2所示。为便于研究,取其中1个矩形裂缝进行钻井液漏失行为分析(图 2中,L为裂缝长度,mm;H为裂缝高度,mm;α为裂缝倾角,(°))。
|
| 图 2 平面裂缝漏失示意 Fig.2 Schematic diagram for losses of drilling fluid through plane fractures |
选取赫-巴模式描述钻井液的流变性[18],其为三参数模式,可以简化为现场常用的宾汉和幂律流变模式,且比宾汉模式和幂律模式能更好地描述钻井液的流变行为。该模式可以表示为:
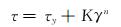
|
(2) |
式中:τ为剪切应力,Pa;τy为动切力,Pa;n为流性指数;K为稠度系数,Pa·sn;γ为剪切速率,s-1。
裂缝存在应力敏感性,钻井液发生漏失,缝内压力升高,造成裂缝宽度增大,裂缝宽度增大进一步促使钻井液漏失,建立模型时需要考虑这个耦合过程。目前,常用线性变形和指数变形方程描述裂缝应力敏感性。为了更真实地描述裂缝宽度的变化行为,笔者采用了指数变形方程,即:

|
(3) |
式中:w0为裂缝法向应力为0时的裂缝宽度,mm;pf为流体压力,MPa;σn为裂缝面法向应力,MPa;β为经验系数,通过试验获取。
2.2 控制方程1) 连续性方程。根据质量守恒原理,连续性方程为:
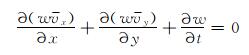
|
(4) |
式中:vx为x方向的平均流速,m/s;vy为y方向的平均流速,m/s;t为时间变量,s。
2) 动量方程。对于赫-巴模式钻井液,其在裂缝内的流速为:
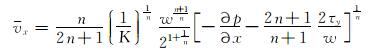
|
(5) |
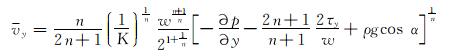
|
(6) |
3) 漏失控制方程。将式(3)、式(5) 和式(6) 代入式(4),可得钻井液漏失控制方程:
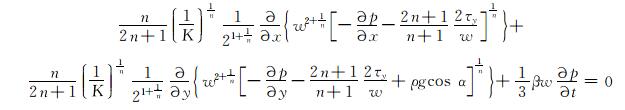
|
(7) |
式(7) 中,裂缝宽度w可根据分形理论由式(1) 求得。进一步讲,w是粗糙裂缝在x,y平面上的裂缝宽度分布函数,表征了裂缝的粗糙程度。
2.3 初始及边界条件根据实际情况,裂缝内的初始压力均为地层压力。假设与井眼相交裂缝的边界条件为:

|
(8) |
式中:p0为地层压力,MPa;pw为井筒压力,MPa;tε为压力逐步升高的时间,s。
其他边界条件为:
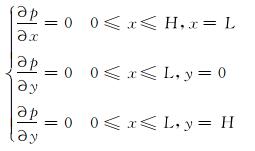
|
(9) |
使用中心差分法对钻井液漏失控制方程进行离散,可得:
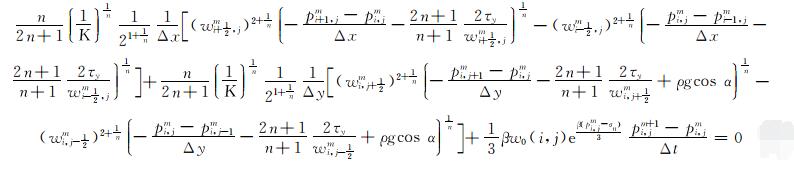
|
(10) |
式(10) 中,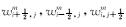
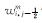
利用粗糙裂缝漏失模型模拟赫-巴模式钻井液的漏失规律,模型中的数据取值见表 1。通过改变模型的网格尺寸、标准差和分形维数,研究裂缝粗糙度对漏失的影响。
| 参数 | 取值 |
| 裂缝长度L/m | 100 |
| 裂缝高度H/m | 100 |
| 预设缝宽wm/mm | 1 |
| 标准差σ/mm | 0.1 |
| 分形维数D | 2.5 |
| 指数变形系数β | 1.0×10-7 |
| 流性指数n | 0.8 |
| 稠度系数K/(Pa·sn) | 0.1 |
| 动切力τy/Pa | 10 |
| 裂缝倾角α/(°) | 0 |
| 井筒压力pw/MPa | 30 |
| 地层压力p0/MPa | 20 |
| 法向应力σn/MPa | 35 |
| x方向步长Δx/m | 3.125 |
| y方向步长Δy/m | 3.125 |
| 时间步长Δt/s | 0.001 |
| 模拟时间t/s | 10 |
| 压力增加时间tε/s | 1 |
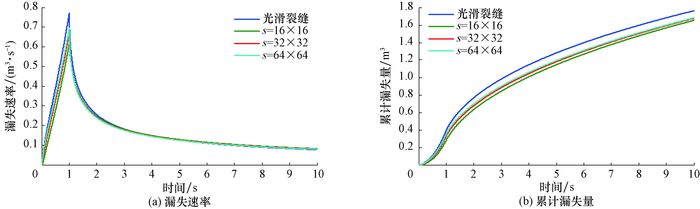
模拟光滑裂缝和网格尺寸为16×16、32×32和64×64的粗糙裂缝的形态和钻井液漏失规律,并统计不同网格尺寸的裂缝宽度,结果见图 3、图 4和表 2。由图 3、图 4和表 2可看出,网格尺寸对裂缝形态无影响,但影响裂缝宽度;网格尺寸变小(网格数增加),裂缝平均宽度变大,标准差变小,漏失速率及累计漏失量变大;网格数大于32×32时,粗糙裂缝的平均宽度与光滑裂缝的缝宽相比误差小于0.86%,峰值漏失速率与更小网格尺寸的漏失速率相比误差小于3.5%,10 s时的漏失量与更小网格尺寸的漏失量相比误差小于3.7%。因此,选择32×32的网格尺寸进行数值模拟能够满足要求。

|
| 图 3 不同网格尺寸下的粗糙裂缝 Fig.3 Rough fracture in different mesh sizes |
|
| 图 4 不同网格尺寸下的钻井液漏失规律 Fig.4 Patterns of drilling fluid losses in different mesh sizes |
| 网格尺寸 | 平均缝宽/ mm | 最小缝宽/ mm | 最大缝宽/ mm | 标准差/ mm | 裂缝体积/ m3 |
| 光滑裂缝 | 1 | 1 | 1 | 0 | 10 |
| 16×16 | 0.988 4 | 0.763 3 | 1.282 2 | 0.075 2 | 9.883 6 |
| 32×32 | 0.991 4 | 0.770 1 | 1.245 2 | 0.070 9 | 9.913 6 |
| 64×64 | 0.992 2 | 0.756 2 | 1.233 0 | 0.068 4 | 9.922 0 |
标准差增大,裂缝起伏程度增加,部分裂缝面与基准面开始接触。假设接触处的最小裂缝宽度为0.001 mm,通过改变标准差预设值的大小,可得到粗糙裂缝(不同标准差的裂缝宽度分布见表 3)。模拟表明,当真实标准差大于0.5 mm时,裂缝面已与基准面开始接触。
| 编号 | 标准差/mm | 平均缝宽/mm | 接触率,% | 最小缝宽/mm | 最大缝宽/mm | 裂缝体积/m3 | |||
| 预设 | 实际 | 预设 | 实际 | ||||||
| Std01 | 0.100 0 | 0.070 8 | 1.008 7 | 1.000 0 | 0 | 0.778 8 | 1.253 9 | 10.000 0 | |
| Std03 | 0.300 0 | 0.212 6 | 1.026 0 | 1.000 0 | 0 | 0.336 3 | 1.761 6 | 10.000 0 | |
| Std07 | 0.700 0 | 0.487 8 | 1.056 9 | 1.000 0 | 1.9 | 0.001 0 | 2.773 5 | 10.000 5 | |
| Std10 | 1.000 0 | 0.671 9 | 1.066 8 | 1.000 0 | 5.6 | 0.001 0 | 3.519 1 | 10.000 9 | |
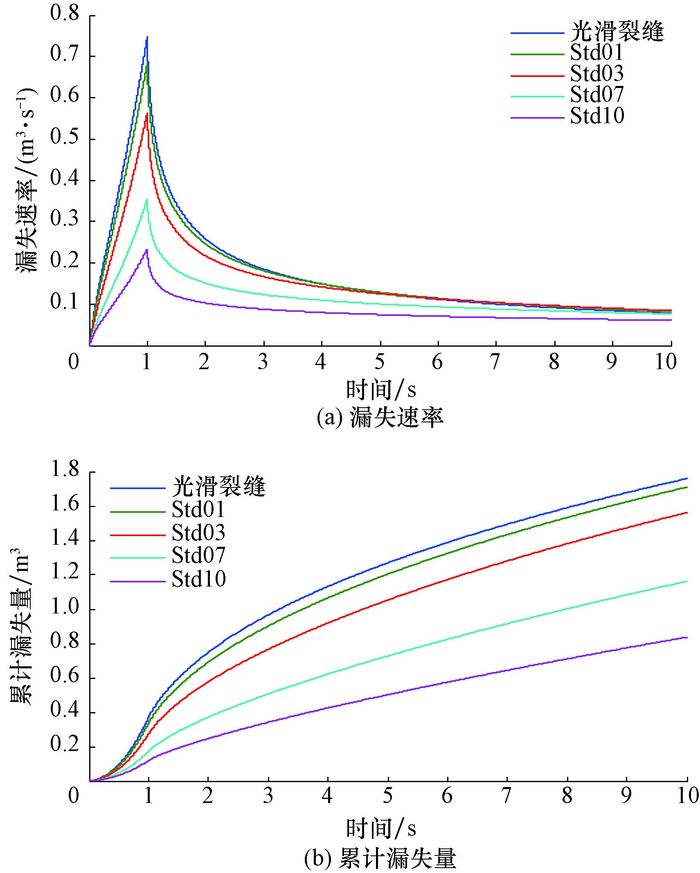
不同标准差下的漏失规律如图 5所示。从图 5可以看出,随着标准差增大,漏失速率和漏失量均明显变小。结合模拟计算得到的流体流线分布图分析可知,这是因为随着标准差增大,裂缝面部分接触,钻井液的流动路线变得越来越复杂,尤其当裂缝面接触后,流动路线的弯曲程度显著增加,导致漏失速率和漏失量显著减小。
|
| 图 5 不同标准差下的漏失规律 Fig.5 Patterns of drilling fluid losses with different standard deviations |
对光滑裂缝和分形维数为2.2、2.5和2.7的裂缝进行模拟,并对裂缝宽度数据进行统计,结果见表 4。由表 4可看出,随着分形维数增大,裂缝平均宽度和裂缝的标准差增大。
| 分形维数 | 平均缝宽/ mm | 最小缝宽/ mm | 最大缝宽/ mm | 标准差/ mm | 裂缝体积/ m3 |
| 光滑裂缝 | 1 | 1 | 1 | 0 | 10 |
| 2.2 | 0.981 9 | 0.818 0 | 1.179 2 | 0.488 4 | 9.819 1 |
| 2.5 | 0.991 3 | 0.770 1 | 1.245 2 | 0.708 8 | 9.913 6 |
| 2.7 | 0.999 6 | 0.722 4 | 1.312 9 | 0.100 1 | 9.995 8 |
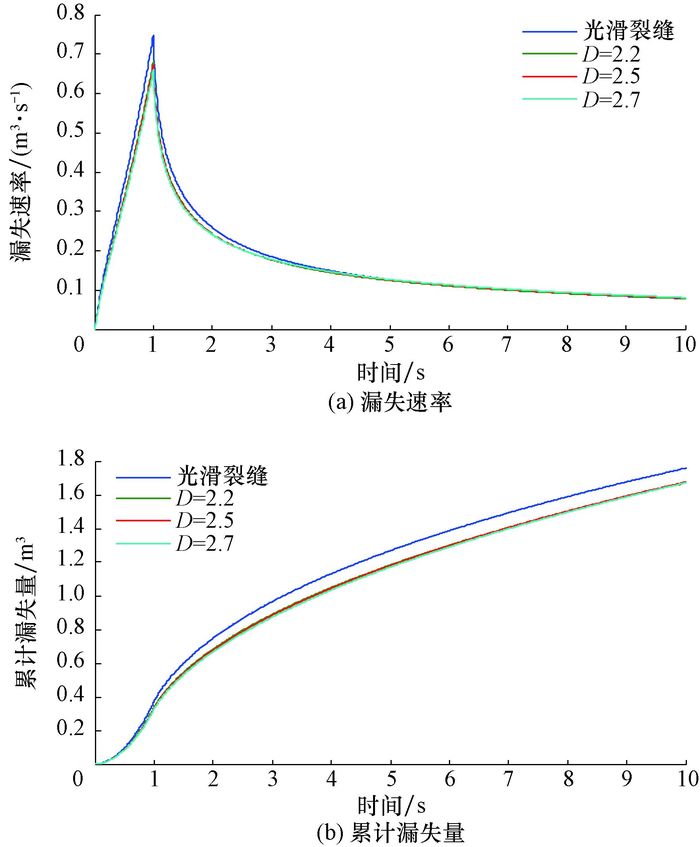
标准差分别为0.1和0.7 mm时不同分形维数下的赫-巴流体漏失规律如图 6和图 7所示。
|
| 图 6 标准差为0.1 mm时不同分形维数下的赫-巴流体漏失规律 Fig.6 Patterns of Herschel-Bulkley fluid losses in different fractal dimensions with standard deviation of 0.1 mm |

|
| 图 7 标准差为0.7 mm时不同分形维数下的赫-巴流体漏失规律 Fig.7 Patterns of Herschel-Bulkley fluid losses in different fractal dimensions with standard deviation of 0.7 mm |
从图 6和图 7可以看出:分形维数对漏失有影响,随着分形维数增加,虽然裂缝平均宽度增大,但漏失速率及累计漏失量仍呈减小趋势。由表 3可知,图 6反映的是裂缝面与基准面未接触的情形,而图 7为裂缝面与基准面有接触的情形。由图 6和图 7可以看出:裂缝面与基准面未接触时,裂缝分形维数对漏失影响不大;裂缝面与基准面接触后,裂缝分形维数对漏失的影响十分显著。
3.4 参数敏感性分析因为早期的漏失速率和漏失量对堵漏措施的选择更为重要,故分析标准差和分形维数对钻井液峰值漏失速率(1 s)和漏失量(10 s)的影响程度,结果见图 8。

|
| 图 8 参数敏感性分析结果 Fig.8 Parameter sensitivity analysis |
图 8表明:随着标准差增大,漏失速率和漏失量近似呈线性减少;随着分形维数增加,漏失速率和漏失量亦近似呈线性减小;标准差越大,分形维数的影响也越大。
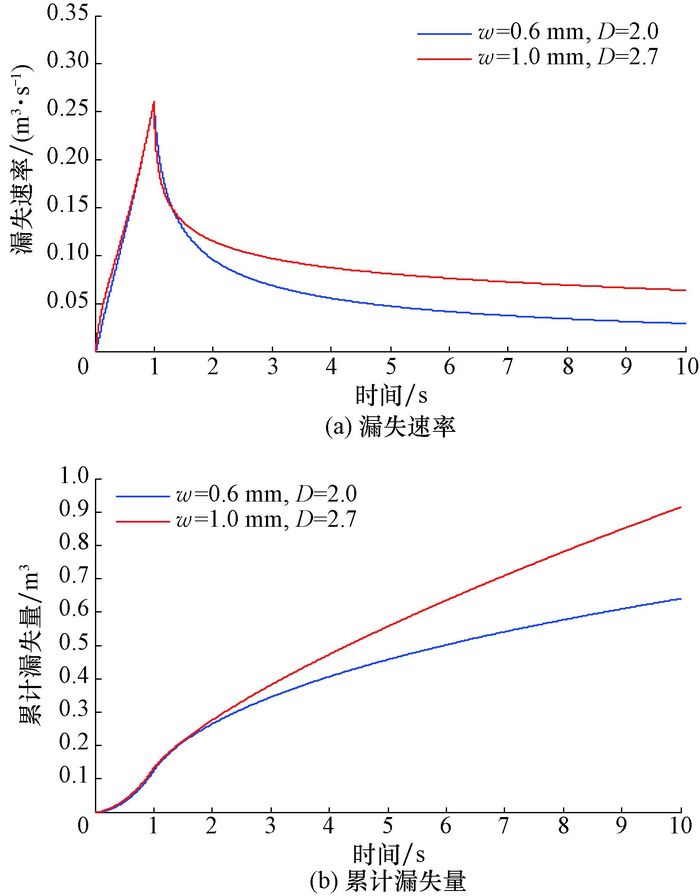
3.5 应用探讨以上研究表明,裂缝平均宽度相同、但标准差和分形维数不同时,相同时刻的漏失速率和漏失量明显不同。因此,漏失速率、漏失量相同时,裂缝平均宽度可以相差较大。例如,平均缝宽为1.0 mm、分形维数为2.7、标准差为0.7 mm的裂缝,峰值漏失速率为0.26 m2/s,而平均缝宽为0.6 mm的光滑裂缝,峰值漏失速率亦为0.26 m2/s,两者的漏失规律如图 9所示。
|
| 图 9 不同裂缝的漏失规律 Fig.9 Patterns of fluid losses in different fractures |
由图 9可知,两者在漏失早期的漏失曲线基本重合。现场应用时,如果仅利用早期漏失速率会导致裂缝宽度预测出现误差。这也说明,具有相同漏失速率及漏失特征的井漏,裂缝平均宽度可能差异较大。如果漏失速率数据有限,现场进行防漏堵漏作业时,应根据裂缝的粗糙度,对预测的裂缝宽度进行适度校正,从而采取合理的防漏堵漏方案。
4 结论与建议1) 利用分形理论构建粗糙裂缝,采用赫-巴流变模式和指数变形方程描述钻井液的流变特性和裂缝的变形特征,根据质量、动量守恒原理,建立了粗糙裂缝钻井液漏失模型,为研究漏失规律及更准确地反演裂缝宽度等提供了理论依据。
2) 裂缝网格尺寸对漏失模拟结果有影响。网格尺寸越小,裂缝漏失速率和漏失量越大。选择32×32的网格尺寸,误差能够满足漏失模拟的需求。
3) 标准差和分形维数都表征裂缝的粗糙程度。随标准差和分形维数增大,裂缝面由未接触向部分接触发展。
4) 标准差和分形维数对漏失均有影响。随着标准差和分形维数增加,钻井液漏失速率及漏失量均近似呈线性减小;但裂缝面没有接触时,分形维数的影响程度比较小。
| [1] |
徐同台, 刘玉杰, 申威, 等.
钻井工程防漏堵漏技术[M]. 北京: 石油工业出版社, 1997: 1-4.
XU Tongtai, LIU Yujie, SHEN Wei, et al. Technology of lost circulation prevention and control during drilling engineering[M]. Beijing: Petroleum Industry Press, 1997: 1-4. |
| [2] |
刘金华, 刘四海, 龙大清, 等.
明1井交联成膜与化学固结承压堵漏技术[J]. 石油钻探技术, 2017, 45(2): 54–60.
LIU Jinhua, LIU Sihai, LONG Daqing, et al. Strengthening plugging operations by combining cross-linked film and chemical consolidation in Well Ming-1[J]. Petroleum Drilling Techniques, 2017, 45(2): 54–60. |
| [3] |
金军斌.
塔里木盆地顺北区块超深井火成岩钻井液技术[J]. 石油钻探技术, 2016, 44(6): 17–23.
JIN Junbin. Drilling fluid technology for igneous rocks in ultra-deep wells in the Shunbei Area, Tarim Basin[J]. Petroleum Drilling Techniques, 2016, 44(6): 17–23. |
| [4] |
杨力.
彭水区块页岩气水平井防漏堵漏技术探讨[J]. 石油钻探技术, 2013, 41(5): 16–20.
YANG Li. Leak prevention and plugging techniques for shale gas horizontal wells in Pengshui Block[J]. Petroleum Drilling Techniques, 2013, 41(5): 16–20. |
| [5] |
王业众, 康毅力, 游利军, 等.
裂缝性储层漏失机理及控制技术研究进展[J]. 钻井液与完井液, 2007, 24(4): 74–77.
WANG Yezhong, KANG Yili, YOU Lijun, et al. Progresses in mechanism study and control:mud losses to fractured reservoirs[J]. Drilling Fluid & Completion Fluid, 2007, 24(4): 74–77. |
| [6] |
韩子轩, 林永学, 柴龙, 等.
裂缝性气藏封缝堵气技术研究[J]. 钻井液与完井液, 2017, 34(1): 16–22.
HAN Zixuan, LIN Yongxue, CHAI Long, et al. Plugging micro-fractures to prevent gas-cut in fractured gas reservoir drilling[J]. Drilling Fluid & Completion Fluid, 2017, 34(1): 16–22. |
| [7] |
李大奇, 刘四海, 林永学, 等.
裂缝网络地层钻井液漏失模拟[J]. 钻井液与完井液, 2017, 34(2): 45–50.
LI Daqi, LIU Sihai, LIN Yongxue, et al. Simulation of mud loss in formations with fracture network[J]. Drilling Fluid & Completion Fluid, 2017, 34(2): 45–50. |
| [8] | LIETARD O, UNWIN T, GUILLOT D, et al.Fracture width LWD and drilling mud/LCM selection guidelines in naturally fractured reservoirs[R].SPE 36832, 1996. |
| [9] | SANFILLIPPO F, BRIGNOLI M, SANTARELLI F J, et al.Characterization of conductive fractures while drilling[R].SPE 38177, 1997. |
| [10] |
李大奇, 康毅力, 刘修善, 等.
裂缝性地层钻井液漏失动力学模型研究进展[J]. 石油钻探技术, 2013, 41(4): 42–47.
LI Daqi, KANG Yili, LIU Xiushan, et al. Progress in drilling fluid loss dynamics model for fractured formations[J]. Petroleum Drilling Techniques, 2013, 41(4): 42–47. |
| [11] |
李松, 康毅力, 李大奇, 等.
裂缝性地层H-B流型钻井液漏失流动模型及实验模拟[J]. 石油钻采工艺, 2015, 37(6): 57–62.
LI Song, KANG Yili, LI Daqi, et al. Flow model and experimental simulation for leak-off of H-B flow-pattern drilling fluid in fractured formation[J]. Oil Drilling & Production Technology, 2015, 37(6): 57–62. |
| [12] | LAVROV A. Newtonian fluid flow from an arbitrarily-oriented fracture into a single sink[J]. Acta Mechanica, 2006, 186(1/2/3/4)): 55–74. |
| [13] | OZDEMIRTAS M, BABADAGLI T, KURU E. Experimental and numerical investigations of borehole ballooning in rough fractures[J]. SPE Drilling & Completion, 2009, 24(2): 256–265. |
| [14] |
贾利春, 陈勉, 侯冰, 等.
裂缝性地层钻井液漏失模型及漏失规律[J]. 石油勘探与开发, 2014, 41(1): 95–101.
JIA Lichun, CHEN Mian, HOU Bing, et al. Drilling fluid loss model and loss dynamic behavior in fractured formations[J]. Petroleum Exploration and Development, 2014, 41(1): 95–101. DOI:10.11698/PED.2014.01.12 |
| [15] | BROWN S R. Fluid flow through rock joints:the effect of surface roughness[J]. Journal of Geophysical Research, 1987, 92(B2): 1337–1348. DOI:10.1029/JB092iB02p01337 |
| [16] |
周志芳, 王锦国.
裂隙介质水动力学[M]. 北京: 中国水利水电出版社, 2004: 101-102.
ZHOU Zhifang, WANG Jinguo. Fissure medium hydrodynamics[M]. Beijing: China Water & Power Press, 2004: 101-102. |
| [17] | PEITGEN H, SAUPE D. The science of fractal images[M]. New York: Springer-Verlag, 1988: 71-133. |
| [18] |
鄢捷年.
钻井液工艺学[M]. 东营: 石油大学出版社, 2001: 77-78.
YAN Jienian. Drilling fluid technology[M]. Dongying: Petroleum University Press, 2001: 77-78. |




