注水开发过程中,水淹层混合液的电阻率是求取剩余油饱和度的重要参数[1-6]。某些地区由于注入水的矿化度与原始地层水存在明显差异,加之缺少用于计算地层水电阻率的自然电位测井资料,导致储层水淹后混合液的电阻率难以确定,造成基于电阻率测井资料计算出的剩余油饱和度精度降低。针对这种情况,一般采用注入水与束缚水并联导电模型或二者充分混合导电模型来计算水淹层混合液的电阻率[7-11]。虽然注入水与束缚水的并联导电模型或二者充分混合导电模型符合一般认识,但这2种模型未充分考虑水淹过程中注入水与束缚水在岩石孔隙内混合的复杂性。在实际水淹过程中,随着含水饱和度增大,储层孔隙内注入水与原生束缚水的混合情况极为复杂,其导电方式是否遵循独立并联导电模型或充分混合导电模型并未得到证实。为此,笔者通过W油田岩心水驱油试验分析了水淹过程中混合液电阻率的变化规律及影响因素,并在此基础上对并联导电模型进行改进,建立了混合液电阻率Rwz与含水饱和度Swz、束缚水饱和度Swi、注入水电阻率Rwj和束缚水电阻率Rwi之间的关系,以解决水淹层混合液电阻率难以确定的问题,从而提高剩余油饱和度的计算精度。
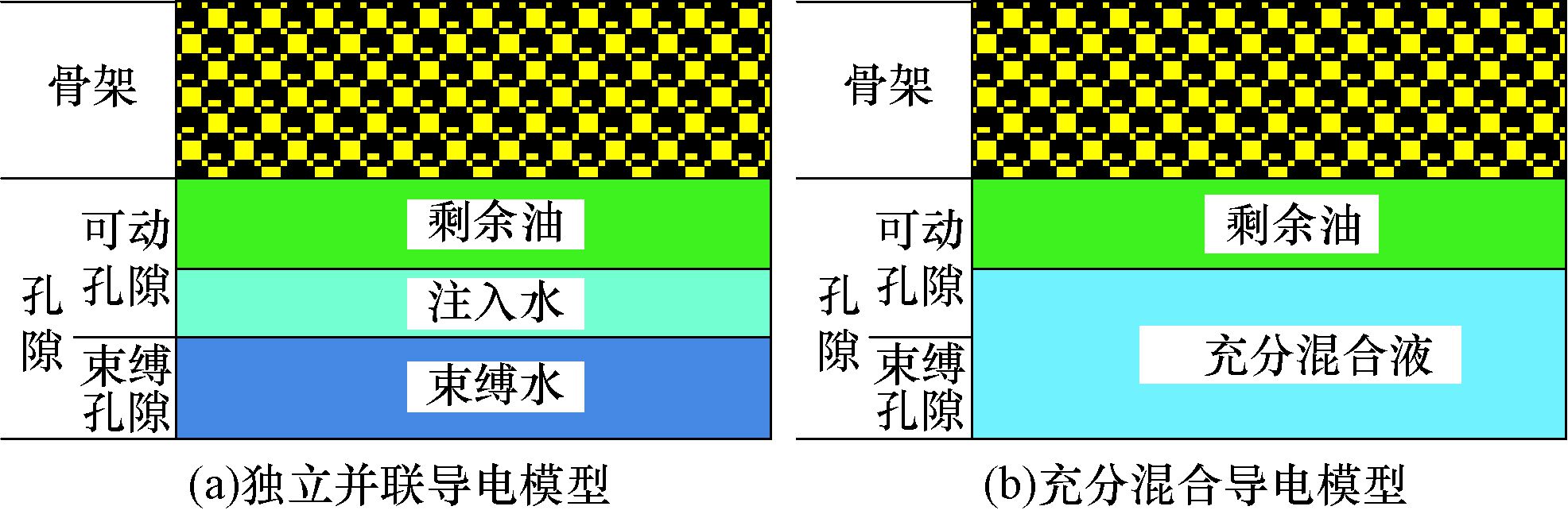
1 水淹层混合液电阻率常规计算方法独立并联导电模型的理论基础是在水淹过程中注入水只驱替孔隙内的可动原油,不与原生束缚水发生混合[7-9](见图 1(a))。因此,水淹层混合液的电阻率为二者并联而成,其导电模型为:
|
| 图 1 独立并联导电模型与充分混合导电模型的基本原理 Fig.1 Basic principles of independent parallel conduction model and fully mixed conduction model |

|
(1) |
式中:Sw和Swi分别为含水饱和度和束缚水饱和度;Rwi,Rwj和Rwz分别为束缚水、注入水和等效混合液的电阻率,Ω·m。
充分混合导电模型的理论基础是在水淹过程中2种不同浓度电解质溶液在储层孔隙内发生离子交换,并且快速达到浓度平衡[10-11](见图 1(b))。因此根据物质平衡原理,混合后溶液中的离子总数等于混合前2种溶液的离子数之和,即:
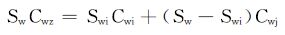
|
(2) |
式中:Cwi,Cwj和Cwz分别为束缚水、注入水和等效混合液的矿化度,mg/L。
在温度已知的条件下,溶液的电阻率与矿化度具有一一对应的关系,利用这种关系就可以计算出混合液的电阻率。
独立并联导电模型和充分混合导电模型在计算水淹层混合液电阻率中得到了较为广泛的应用,但目前存在2点争议:1)2种矿化度存在差异的电解质溶液在孔隙内接触后,其间应该存在离子交换[12-13],不可能完全独立;2)虽然将2种矿化度有差异的溶液放入同一容器后,在一定时间内二者能够充分均匀混合(达到离子浓度平衡),但与简单的容器相比,储层的孔隙结构异常复杂,注入水与束缚水在孔隙内能否快速达到充分均匀混合的状态,目前尚未得到试验证实。因此,有必要开展地层温度和压力条件下的水驱油试验进行相关分析。
2 水驱油试验 2.1 试验方法及试验结果海上某砂岩油田W油田的开发方式为典型的注海水开发,且属于注入水矿化度明显高于地层水矿化度的情况。利用该油田岩心模拟储层温度和压力进行水驱油试验,以分析注海水条件下岩石电阻率的变化规律。
试验步骤为:1)将岩样洗油、洗盐、烘干,测定孔隙度和渗透率,并利用平行岩样进行粒度分析,以测量泥质含量;2)将饱和地层水的岩样抽真空饱和地层水(地层水矿化度约为15 600 mg/L),并测定饱和地层水岩样的电阻率;3)将饱和地层水的岩样放入夹持器,加温、加压至储层条件(温度109 ℃、围压33 MPa),用W油田的产出油驱替岩样中的水,出水量达到不同预定值时(即预定不同含水饱和度),暂停驱替,等待电阻率测试仪读数稳定后记录岩样在不同含水饱和度下的电阻率,直至岩样出口端不再出水(岩样已饱和油至束缚水状态)后停止驱替,并测定此时岩样的电阻率;4)然后用海水配制矿化度约为33 500 mg/L的水(注入水)驱替岩样,出水量达到不同预定值时(即预定不同含水饱和度),暂停驱替,等待电阻率测试仪读数稳定后记录岩样在不同含水饱和度下的电阻率,直至岩样出口端达到预计出水总量或不再出油后停止驱替。
选取能代表W油田物性分布的3块岩样进行测试分析,表 1为这3块岩样的物性参数及电阻率。
| 样品编号 | 孔隙度,% | 渗透率/mD | 泥质含量,% | 束缚水饱和度,% | 残余油饱和度,% | 电阻率/(Ω·m) | |
| 完全饱和水 | 饱和油至束缚水 | ||||||
| 1 | 16.5 | 3.5 | 11.9 | 47.1 | 29.4 | 4.3 | 16.9 |
| 2 | 17.8 | 25.7 | 6.1 | 38.0 | 36.6 | 3.3 | 19.5 |
| 3 | 19.1 | 154.1 | 7.8 | 31.9 | 33.9 | 2.8 | 20.1 |
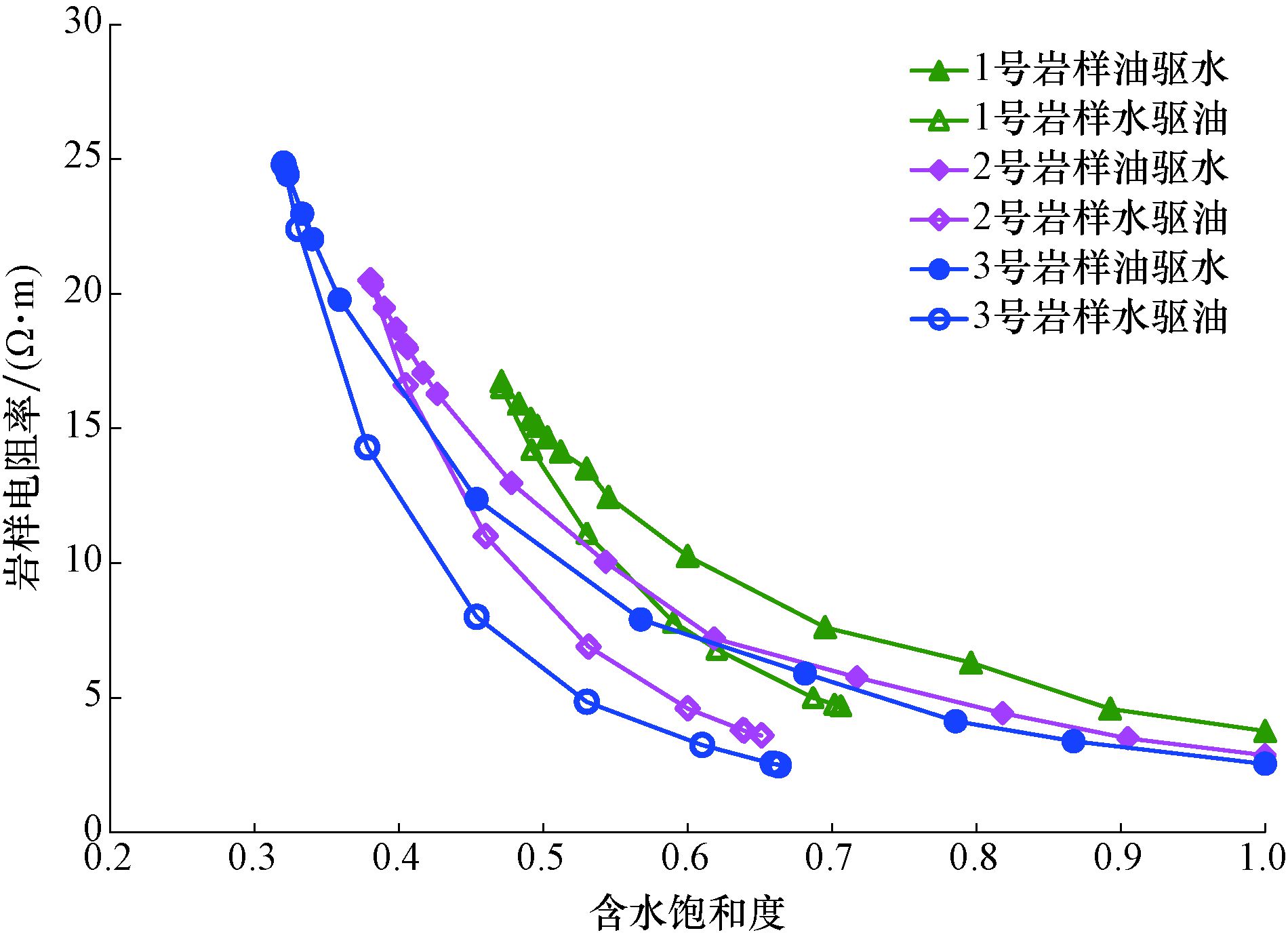
图 2为3块岩样在模拟成藏(油驱水)和开发(水驱油)过程中岩样电阻率随含水饱和度变化的曲线。
|
| 图 2 油驱水和水驱油过程中岩样电阻率与含水饱和度的关系 Fig.2 The relationship between rock resistivity and water saturation during the process of oil displacement by water and water displacement by oil |
由图 2可以看出:
1) 物性越好的岩样,其完全饱和水时的电阻率越低,而当饱和油至束缚水状态时的电阻率越高。这是由于物性好的岩样孔隙结构相对较简单,连通性好,完全饱和水时,岩样孔隙内水形成的导电电路更畅通,因此电阻率更低;而饱和油至束缚水状态时,岩样的导电性主要受孔隙内束缚水的影响,物性越好,束缚水越低,因此导电性越差[14-17]。
2) 在水驱油过程中,随含水饱和度增大,3块岩样的电阻率均呈单调下降趋势,且当含水饱和度一定时,均出现了比油驱水时电阻率低的现象。这是由于随着孔隙内水体积增大,导电电路变得更发达。同时,进入孔隙内注入水的矿化度高于原生束缚水的矿化度,对地层水起到了“咸化”作用,二者形成等效混合液的电阻率低于原生束缚水的电阻率,从而增强了导电性[18-19]。
3) 在水驱油过程中,当驱替至残余油状态(完全水淹)时,岩样的物性越好,电阻率越低,3号岩样此时的电阻率甚至低于该岩样完全饱和原生地层水时的电阻率。这是由于当驱替至残余油状态时,岩样的物性越好,可动水饱和度与束缚水饱和度比值越大,对原生束缚水的“咸化”作用更强,形成等效混合液的电阻率更低。
2.2 混合液电阻率变化规律分析笔者利用水驱油试验过程中测量的电阻率与含水饱和度数据,选用适合于该油田的饱和度计算公式,反推岩样在水淹过程中等效混合液的电阻率,研究水淹过程中混合液电阻率随含水饱和度增加的变化规律,并利用计算得到的混合液电阻率验证独立并联导电模型和充分混合导电模型的适用性。由于W油田储层岩性较细,泥质主要以层状泥质与分散泥质混合形式存在,根据其他地区的经验[20-21],印度尼西亚公式适合于计算该油田的含水饱和度。
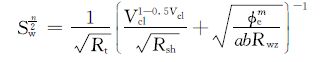
|
(3) |
式中:Sw为含水饱和度;Rt和Rsh分别代表原状地层和泥岩的电阻率,Ω·m;Vcl为储层泥质含量;a,b,m和n分别为岩性系数、与岩性有关的常数、胶结指数和饱和度指数;φe为有效孔隙度。
式(3)变形可得水淹层混合液电阻率的计算公式:

|
(4) |
W油田纯泥岩电阻率Rsh取2.5 Ω·m;Vcl通过分析平行岩样的粒度得到(见表 1)。通过模拟该油田油藏温度和压力条件下的岩电试验测得a=1.1,m=1.91,b=0.99,n=1.63。
利用独立并联导电模型、充分混合模型和印度尼西亚公式计算3块岩样在水驱油过程中不同含水饱和度下等效混合液的电阻率,结果见图 3,其中,实线表示利用印度尼西亚公式(式(4))反推出的等效混合液电阻率Rwz,短虚线为利用并联导电模型(式(1))计算出的混合液电阻率Rwz1,长虚线为按照充分混合理论(式(2))计算出的混合液电阻率Rwz2。
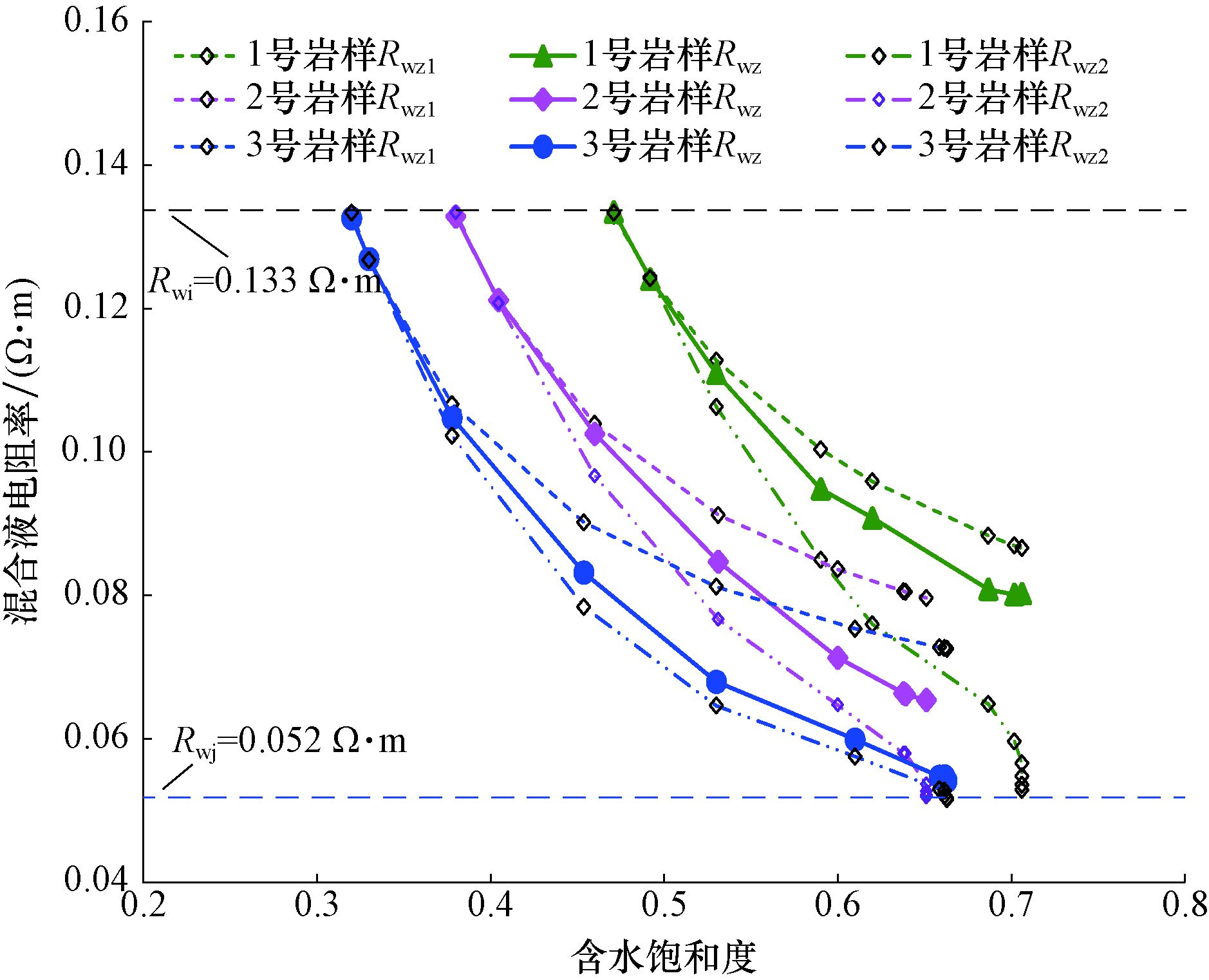
|
| 图 3 水驱油过程中混合液电阻率的变化特征 Fig.3 Variation characteristics of resistivity in mixed liquid during the water flooding process |
由图 3可以看出:1)由于注入水矿化度大于束缚水矿化度,计算出3块岩样等效混合液的电阻率Rwz均随着含水饱和度增大而单调降低;2)Rwz始终介于Rwz1和Rwz2之间,三者的关系为Rwz2≤Rwz≤Rwz1,说明在水淹过程中注入水与束缚水之间存在离子交换,并非完全独立,但也未达到充分混合的状态;3)3块岩样最初的Rwz均为束缚水电阻率,但随着水驱油的进行,随含水饱和度增大,3号岩样混合液电阻率的降低幅度最大,2号次之,1号最小,且当驱替至残余油状态时3号岩样混合液的电阻率接近于注入水电阻率。这表明在水驱油过程中,物性好的岩样孔隙连通性好,在相同驱替强度下更容易水淹[22-24],含水饱和度增加幅度大,同时束缚水饱和度也更低。
3 混合液电阻率与剩余油饱和度的确定水驱油试验数据分析表明,在水淹过程中,储层孔隙内注入水与束缚水的混合是一个复杂而又连续的过程,应介于完全独立和充分混合2种状态之间。在含泥质砂岩油层中,随着水淹程度增强,含水饱和度升高,由于存在矿化度差异发生离子交换,无论是毛细管束缚水还是泥质束缚水均会逐渐被注入水所“同化”,但其最终能否完全变为注入水除了与水淹程度有关之外,还与物性有关,物性越好,束缚水越容易被完全“同化”。为此,笔者对并联导电模型进行了改进,如图 4所示。笔者认为在束缚水逐步被“同化”过程中的某一时刻,可将其等效为两部分:一部分是与注入水混合的束缚水,且由于水淹过程中注入水具有连续供应性,这部分水已经完全变成了注入水;另一部分则是未与注入水混合的剩余束缚水,其饱和度用Swb表示,矿化度保持不变。因此,随着水淹程度增强,与注入水混合的束缚水将从0逐渐增大,其饱和度最大能达到Swi(与物性有关,物性越好,束缚水越容易被完全“同化”),而未与注入水混合的剩余束缚水饱和度Swb则从束缚水饱和度Swi逐渐减小至0。
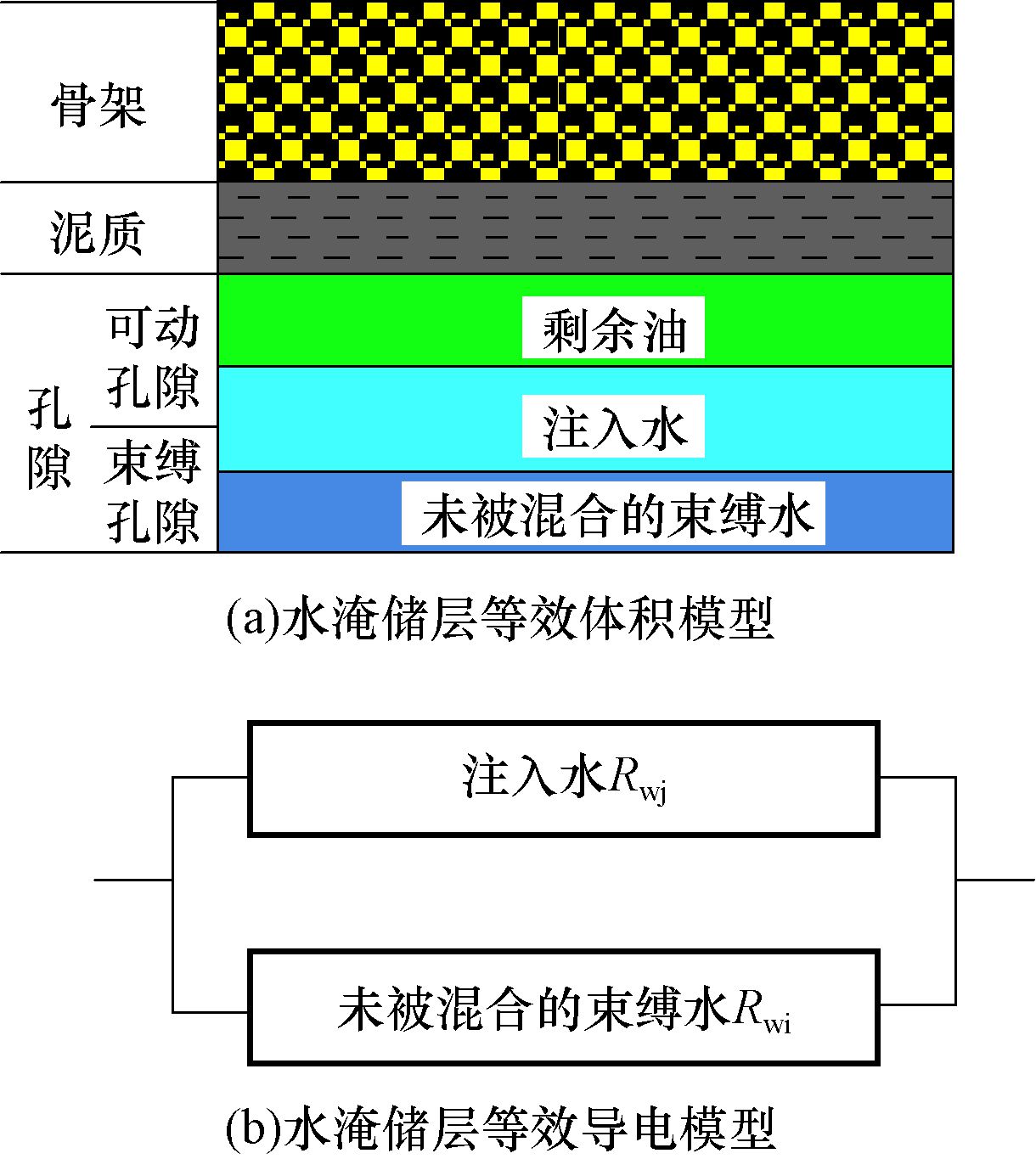
|
| 图 4 储层水淹后等效体积模型与等效导电模型 Fig.4 Equivalent volume model and conductivity model in a water flooded reservoir |
由图 4(b)可知,水淹储层的电阻率由未与注入水混合束缚水的电阻率Rwi和注入水(其包括可动水和被注入水同化的束缚水)的电阻率Rwj并联而成。依据并联导电理论,建立改进的水淹层混合液并联导电模型:
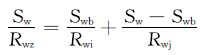
|
(5) |
将式(5)变形,可得到Swb的计算公式:
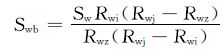
|
(6) |
图 5为3块岩样在水驱油过程中,未与注入水混合束缚水饱和度Swb与含水饱和度Sw的关系曲线。由图 5可以看出,随着Sw增大,水淹程度增强,与注入水混合的束缚水越来越多,Swb越来越低,且物性好的岩样由于孔隙结构相对简单,束缚水容易与注入水混合,导致Swb降低速度快,Swb最终值低,反之,则Swb高。
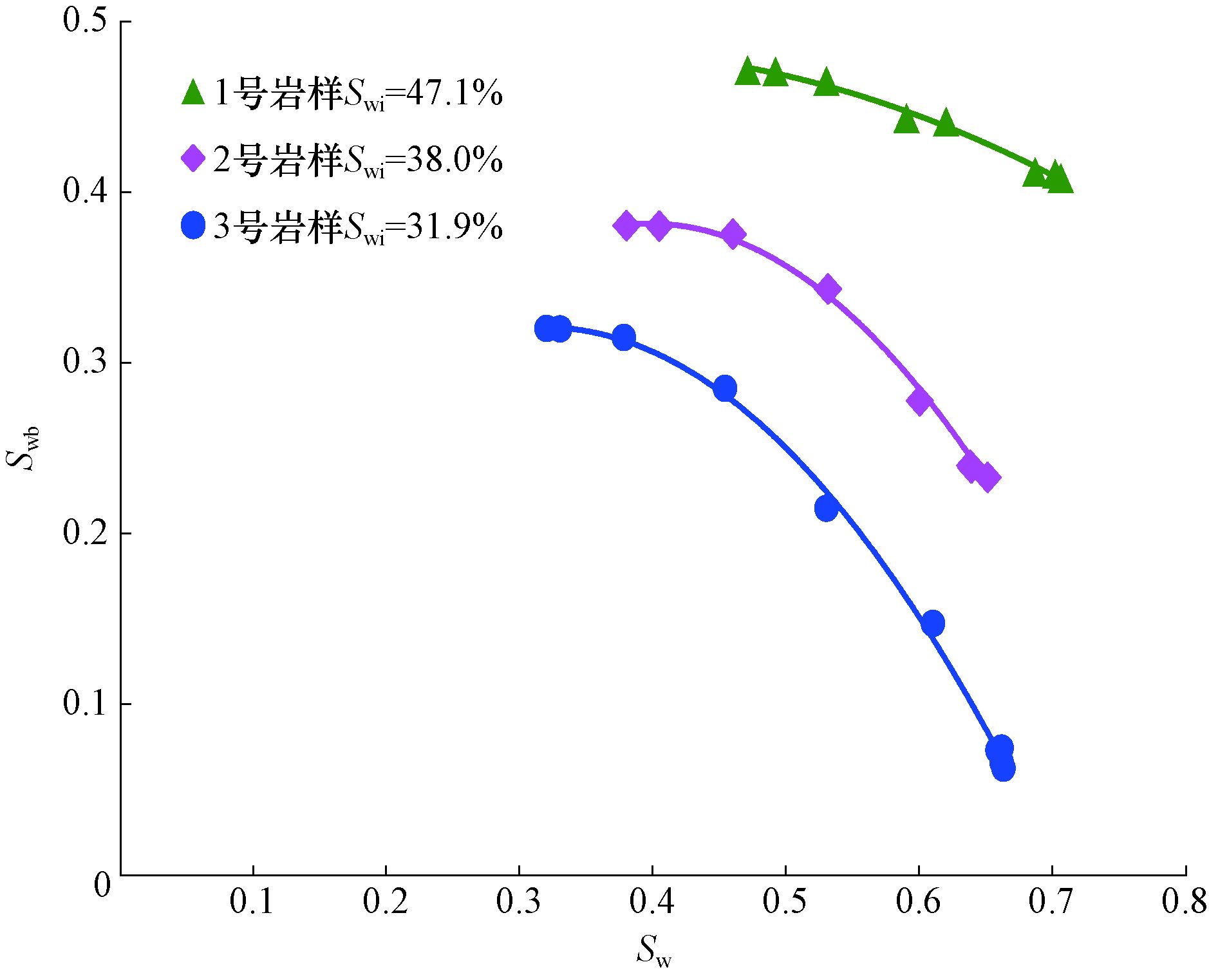
|
| 图 5 未与注入水混合束缚水饱和度Swb与含水饱和度Sw的关系 Fig.5 The relationship between irreducible water saturation Swb and water saturation Sw without mixing with injected water |
由于物性差异导致了束缚水饱和度Swi不同,因此,3个岩样Swb与Sw的关系存在差异。为此,利用多元拟合方法拟合出W油田水淹过程中Swb的计算模型:

|
(7) |
将式(7)代入式(5)可得混合液电阻率Rwz的理论计算公式:

|
(8) |
由式(8)可以看出,水淹层混合液的电阻率Rwz与束缚水电阻率Rwi、注入水电阻率Rwj、束缚水饱和度Swi和当前含水饱和度Sw有关。
联立式(8)和式(3)可计算水淹层的含水饱和度,进而求出剩余油饱和度。式(8)中的Rwi和Rwj可根据矿化度与电阻率的对应关系求出,而Swi可根据储层物性参数计算出,因此,式(8)实际上是混合液电阻率Rwz与当前含水饱和度Sw的函数关系式。印度尼西亚公式(式(3))中的岩电参数(a,b,m和n)已经通过岩电试验获得,原状地层电阻率Rt和泥岩电阻率Rsh已知,泥质含量Vcl和孔隙度φe可通过测井曲线计算得到,因此,式(3)亦为Rwz与Sw的关系式。
利用迭代法可求解由式(8)和式(3)组成的方程组,求解具体步骤为:1)假定Rwz的初值为Rwi,即未水淹,并以0.001 Ω·m为步长(可调节),从Rwi到Rwj逐一取值;2)Rwz每取一个定值时,利用式(3)计算出一个Sw值,将该值带入式(8)又可以计算出一个Rwz值,将该Rwz值与步骤1)假定Rwz对比,如此循环,控制误差满足一定精度时停止迭代,此时的Rwz和Sw值即为方程组的最终解。
4 应用实例W油田的主要目的层为W3Ⅳ油组D砂体,于1999年投产,从2005年开始,该油田构造低部的生产井转注海水补充能量,经过多年注海水开发,该油田新投产井初期见水的现象已经日渐明显。目前,W油田生产井的综合含水率已达到74.0%,处于中高含水期。同时,通过研究该油田探井和早期生产井的资料,确定W3Ⅳ油组的电阻率下限为10 Ω·m,典型水层的电阻率为2 Ω·m,而该油田X井目的层的深电阻率仅为3~8 Ω·m,密闭取心证实该井已经发生水淹。利用上文给出的计算方法,求取X井水淹层混合液的电阻率及含水饱和度,结果见图 6。图 6中,第8道为混合液电阻率计算结果,Rwz_G,Rwz_B和Rwz_C分别为利用改进的并联导电模型、独立并联导电模型和充分混合导电模型计算的混合液电阻率。
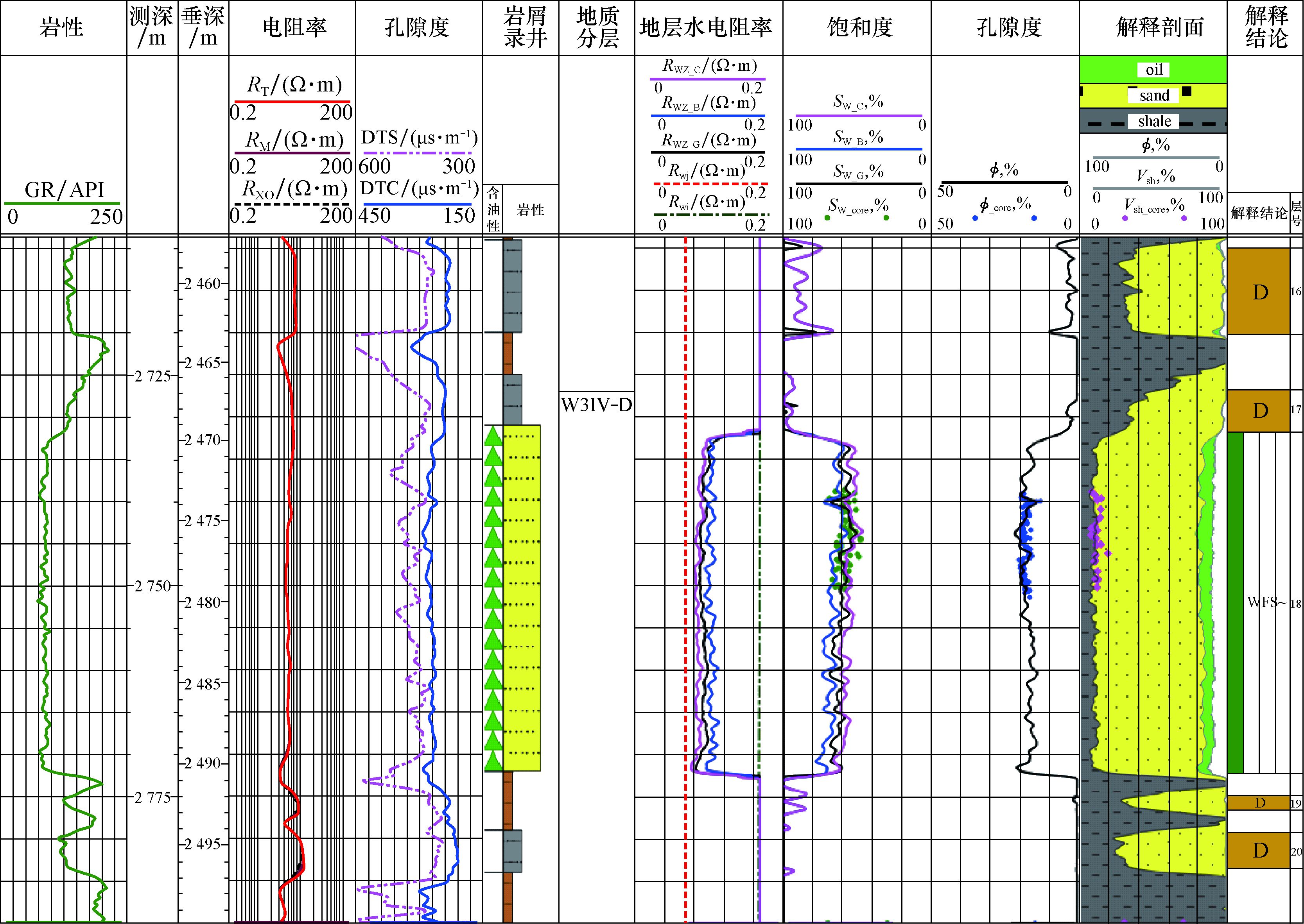
|
| 图 6 W油田X井水淹层解释成果 Fig.6 The interpretation results of water flooded layer in the Well X of W Oilfield |
由图 6可以看出,Rwz_G,Rwz_B和Rwz_C均介于注入水电阻率Rwj与束缚水电阻率Rwi之间,说明利用3种导电模型计算的混合液电阻率均具有一定的合理性。由于充分混合导电模型基于注入水和束缚水时刻保持均匀混合的状态,即注入水对原生束缚水的“同化”作用达到极点,因此,利用该模型计算的混合液电阻率更接近于注入水电阻率;独立并联导电模型基于束缚水始终不会被注入水“同化”,因此利用其计算的混合液电阻率更接近于束缚水电阻率;改进的并联导电模型基于注入水与束缚水介于完全独立和充分混合2种状态之间建立,因此利用其计算的混合液电阻率则介于两者之间,即Rwz_B≤Rwz_G≤Rwz_C,这与上文论述的混合液电阻率变化规律一致。
图 6中的第9道为利用改进的并联导电模型、独立并联导电模型和充分混合导电模型计算的混合液电阻率计算出的含水饱和度,分别为Swz_G、Swz_B和Swz_C。由图 6可以看出,Swz_G与密闭取心样品库仑法分析的含水饱和度Sw_core的吻合度最高。
表 2为X井利用3种导电模型计算含水饱和度的误差统计结果。由表 2可以看出:独立并联导电模型计算含水饱和度的误差分布在2.0%~7.0%,平均为4.5%;充分混合导电模型计算含水饱和度的误差分布在-8.2%~-0.8%,平均为-4.8%;改进的并联导电模型计算含水饱和度的误差分布在-2.7%~5.1%,平均为-0.3%。由此可见,与前2种模型相比,采用改进的并联导电模型计算的含水饱和度精度更高。这也说明,采用改进的并联导电模型可以提高混合液电阻率的计算精度。
| 井段/m | φe,% | Rwz/(Ω·m) | Sw,% | Sw的绝对误差,% | |||||||||
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 1 | 2 | 3 | ||||
| 2 739.00~2 739.70 | 19.7 | 0.099 | 0.086 | 0.092 | 59.2 | 63.6 | 52.3 | 57.9 | 4.4 | -6.9 | -1.3 | ||
| 2 739.70~2 740.50 | 15.6 | 0.098 | 0.088 | 0.098 | 62.3 | 69.3 | 58.4 | 67.4 | 7.0 | -3.9 | 5.1 | ||
| 2 740.50~2 742.80 | 18.8 | 0.105 | 0.092 | 0.096 | 58.2 | 60.2 | 54.2 | 56.8 | 2.0 | -4.0 | -1.4 | ||
| 2 742.80~2 745.00 | 19.9 | 0.097 | 0.084 | 0.089 | 56.8 | 61.6 | 48.6 | 55.1 | 4.8 | -8.2 | -1.7 | ||
| 2 745.00~2 746.80 | 18.2 | 0.096 | 0.082 | 0.088 | 56.5 | 60.1 | 52.3 | 53.8 | 3.6 | -4.2 | -2.7 | ||
| 2 746.80~2 747.70 | 16.7 | 0.103 | 0.087 | 0.093 | 59.4 | 65.6 | 58.6 | 62.3 | 6.2 | -0.8 | 2.9 | ||
| 2 747.70~2 748.30 | 20.9 | 0.095 | 0.081 | 0.087 | 60.7 | 64.9 | 57.9 | 59.2 | 4.2 | -2.8 | -1.5 | ||
| 2 748.30~2 750.80 | 18.6 | 0.099 | 0.082 | 0.087 | 62.2 | 65.7 | 54.5 | 60.4 | 3.5 | -7.7 | -1.8 | ||
| 注:1,2和3分别为采用独立并联导电模型、充分混合导电模型和改进并联导电模型的计算结果;4为密闭取心样品库仑法分析结果。 | |||||||||||||
1) 水驱油试验结果表明,水淹过程中注入水与原生束缚水的混合介于完全独立和充分混合2种状态之间,且物性越好、水淹程度越强的储层,混合程度越高;反之,混合状态越低。
2) 与独立并联导电模型和充分混合导电模型相比,采用改进的并联导电模型计算的水淹层混合液电阻率精度有明显提高,可进行推广应用。
3) 水淹层混合电阻率计算方法是在注入水矿化度大于束缚水矿化度的水驱油试验条上建立的,其是否适用于注入水矿化度小于束缚水矿化度水淹层,有待于通过试验和测试资料验证。
| [1] |
褚人杰, 孙德明, 姜文达.
确定水驱油藏地层混合液电阻率的方法[J]. 测井技术, 1995, 19 (2) : 117–125.
CHU Renjie, SUN Deming, JIANG Wenda. Methods for determining resistivity of mixed formation water in water drive reservoir[J]. Well Logging Technology, 1995, 19 (2) : 117–125. |
| [2] |
郭元岭, 苏国英.
水淹油层含水率解释精度影响因素分析[J]. 石油勘探与开发, 1998, 25 (4) : 59–61.
GUO Yuanling, SU Guoying. An analysis of factors affecting the precision of log interpretation of water cut in a watered out reservoir[J]. Petroleum Exploration and Development, 1998, 25 (4) : 59–61. |
| [3] |
俞军, 史謌, 王伟男.
高含水期地层水电阻率求取方法[J]. 北京大学学报(自然科学版), 2005, 41 (4) : 536–541.
YU Jun, SHI Ge, WANG Weinan. Determination of formation water resistivity during the high water-cut stage[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2005, 41 (4) : 536–541. |
| [4] |
王美珍, 俞军.
用测井资料确定大庆长垣水淹层混合液电阻率[J]. 大庆石油地质与开发, 2007, 26 (2) : 120–122.
WANG Meizhen, YU Jun. Using well logging data to determine resistivity of mixed fluid in water flooded layer of Daqing Placanticline[J]. Petroleum Geology & Oilfield Development in Daqing, 2007, 26 (2) : 120–122. |
| [5] |
张占松, 张超谟.
水淹层地层水电阻率的二步确定方法[J]. 测井技术, 2011, 35 (4) : 340–343.
ZHANG Zhansong, ZHANG Chaomo. Two-step determination method of formation water resistivity in water-flooded zone[J]. Well Logging Technology, 2011, 35 (4) : 340–343. |
| [6] |
宋延杰, 田彦玲, 唐晓敏, 等.
聚合物驱水淹层有效介质电阻率模型[J]. 测井技术, 2009, 33 (3) : 227–232.
SONG Yanjie, TIAN Yanling, TANG Xiaomin, et al. Effective medium resistivity model for water-flooded zone in polymer-flooding oilfield[J]. Well Logging Technology, 2009, 33 (3) : 227–232. |
| [7] |
王敬农.
混合液电导率的实验室研究[J]. 测井技术, 1985, 9 (1) : 42–46.
WANG Jingnong. Laboratory study on the conductivity of mixed liquid[J]. Well Logging Technology, 1985, 9 (1) : 42–46. |
| [8] |
赵文杰.
水淹层岩石电阻率特性的实验研究[J]. 油气采收率技术, 1995, 4 (2) : 32–39.
ZHAO Wenjie. Experiment research on the rock resistivity properties of watered-out formation[J]. Oil & Gas Recovery Technology, 1995, 4 (2) : 32–39. |
| [9] |
杨景强, 卢艳, 马宏宇, 等.
水淹层地层水电阻率变化规律研究[J]. 测井技术, 2006, 30 (3) : 195–197.
YANG Jingqiang, LU Yan, MA Hongyu, et al. On variation regularity of resistivity of mixed formation water in water-flooded zone[J]. Well Logging Technology, 2006, 30 (3) : 195–197. |
| [10] |
邹长春, 尉中良, 潘令枝.
计算混合液电阻率的一种有效方法[J]. 物探化探计算技术, 1999, 21 (3) : 216–219.
ZOU Changchun, WEI Zhongliang, PAN Lingzhi. An effective method to calculate resistivity of mixing solution[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1999, 21 (3) : 216–219. |
| [11] |
申辉林, 方鹏.
水驱油地层电阻率变化规律数值模拟及拐点影响因素分析[J]. 中国石油大学学报(自然科学版), 2011, 35 (3) : 58–62.
SHEN Huilin, FANG Peng. Numerical simulation of formation resistivity variation in water drive process and analysis of influence factors of inflection point[J]. Journal of China University of Petroleum(Edition of Natural Science), 2011, 35 (3) : 58–62. |
| [12] |
孙德明, 胡杰, 陈学义.
淡化系数方程在稠油水淹层测井评价中的应用[J]. 测井技术, 1996, 20 (5) : 341–344.
SUN Deming, HU Jie, CHEN Xueyi. Application of freshening factor equation to calculating residual oil saturation in steam soak reservoir[J]. Well Logging Technology, 1996, 20 (5) : 341–344. |
| [13] |
杨春梅.油田开发中后期测井响应变化机理及储层性质研究[D].北京:中国石油大学(北京),2005:76-80.
YANG Chunmei.Study on reservoir properties and change mechanism of well logging curve in the middle later period of oilfield development[D].Beijing:China University of Petroleum(Beijing),2005:76-80. |
| [14] |
雍世和, 张超谟.
测井数据处理与综合解释[M]. 东营: 石油大学出版社 ,1996 : 127 -133.
YONG Shihe, ZHANG Chaomo. Logging data processing and comprehensive interpretation[M]. Dongying: Petroleum University Press, 1996 : 127 -133. |
| [15] |
宋维琪, 关继腾, 房文静.
注水过程中岩石电性变化规律的理论研究[J]. 石油地球物理勘探, 2000, 35 (6) : 757–762.
SONG Weiqi, GUAN Jiteng, FANG Wenjing. Theoretical study of varying rule for rock resistivity in water injection process[J]. Oil Geophysical Prospecting, 2000, 35 (6) : 757–762. |
| [16] | ARCHIE G E, ZHANG Gengji. The electrical resistivity log as an aid in determining some reservoir characteristics[J]. Well Logging Technology, 2007, 31 (3) : 197–202. |
| [17] |
毛志强, 谭廷栋, 林纯增, 等.
完全含水多孔岩石电学性质及其孔隙结构实验研究[J]. 石油学报, 1997, 18 (3) : 51–55.
MAO Zhiqiang, TAN Tingdong, LIN Chunzeng, et al. The laboratory studies on pore structure and electrical properties of core samples fully-saturated with brine water[J]. Acta Petrolei Sinica, 1997, 18 (3) : 51–55. |
| [18] |
范宜仁, 邓少贵, 周灿灿.
柳东地区岩石电阻率实验及数值模拟研究[J]. 石油大学学报(自然科学版), 1998, 22 (5) : 42–44.
FAN Yiren, DENG Shaogui, ZHOU Cancan. Experimental study on rock resistivity of Liudong Oilfield and digital analogy[J]. Journal of the University of Petroleum,China(Edition of Natural Science), 1998, 22 (5) : 42–44. |
| [19] |
张超谟, 张占松, 郭海敏.
水驱油电阻率与含水饱和度关系的理论推导和数值模拟研究[J]. 中国科学(D辑):地球科学, 2008, 38 (supplement 2) : 151–156.
ZHANG Chaomo, ZHANG Zhansong, GUO Haimin. The study of theory deduction and numerical simulation on the relationship between resistivity and water saturation of water flooding[J]. Science in China (Series D):Earth Sciences, 2008, 38 (supplement 2) : 151–156. |
| [20] |
蔡军, 李茂文, 何胜林.
海水注入开发中剩余油饱和度评价研究[J]. 石油钻采工艺, 2007, 29 (6) : 77–79.
CAI Jun, LI Maowen, HE Shenglin. Research of residual oil saturation evaluation in high salinity water injection development[J]. Oil Drilling & Production Technology, 2007, 29 (6) : 77–79. |
| [21] |
何胜林, 高楚桥, 陈嵘.
涠洲W油田中块剩余油饱和度计算中关键参数确定方法研究[J]. 石油天然气学报, 2011, 33 (12) : 88–91.
HE Shenglin, GAO Chuqiao, CHEN Rong. Method of determining residual oil saturation in the middle block of Weizhou W Oilfield[J]. Journal of Oil and Gas Technology, 2011, 33 (12) : 88–91. |
| [22] |
魏斌, 张友生, 杨贵凯, 等.
储集层流动单元水驱油实验研究[J]. 石油勘探与开发, 2002, 29 (6) : 72–74.
WEI Bin, ZHANG Yousheng, YANG Guikai, et al. Oil-water displacement experiment of reservoir fluid flow unit[J]. Petroleum Exploration and Development, 2002, 29 (6) : 72–74. |
| [23] |
张庆国, 李迎九, 周新茂, 等.
注水开发油田储层水淹主控因素分析[J]. 大庆石油学院学报, 2006, 30 (4) : 98–100.
ZHANG Qingguo, LI Yingjiu, ZHOU Xinmao, et al. Analysis of key factors in water-flooded reservoir in water-driven oil fields[J]. Journal of Daqing Petroleum Institute, 2006, 30 (4) : 98–100. |
| [24] |
黄素, 徐怀民, 王超, 等.
海相深层砂岩油藏开发中后期油层水淹特征[J]. 特种油气藏, 2014, 21 (5) : 107–110.
HUANG Su, XU Huaimin, WANG Chao, et al. Waterflooding features in the middle and late stage of development of deep marine sandstone reservoir[J]. Special Oil & Gas Reservoirs, 2014, 21 (5) : 107–110. |




