2. 中国石油大学(北京)地球科学学院, 北京 102249
2. College of Geosciences, China University of Petroleum(Beijing), Beijing, 102249, China
目前,基于安全考虑,海上钻井作业大多采用过平衡钻井,即钻进过程中钻井液液柱压力大于地层压力,钻井液的密度一般比地层压力当量密度大0.07~0.15 kg/L。虽然过平衡钻井能很好地保持井壁的稳定性,保障钻井安全,但是在过平衡状态下,钻井液滤液会大量侵入储层,对储层造成伤害[1]。观察过平衡钻井条件下所取的西湖凹陷砂岩岩心发现,钻井液滤液侵入较严重[2],并且相同井段在不同时间进行测井所测得的电阻率差别较大,给测井解释中电阻率的取值带来一定困难[3-4],因此有必要对钻井液滤液侵入后的地层电阻率进行校正[5]。国内学者进行了钻井液滤液侵入及其对地层电性影响的相关研究,并取得了一些认识[6-7],但对实际测井获取的电阻率与数值模型的综合研究比较薄弱。为此,笔者基于低渗气层岩心钻井液滤液侵入试验,进行了钻井液滤液侵入数值模拟,根据试验数据、测井数据进行历史拟合,采用拟合后的模型预测钻井液滤液侵入深度,并应用基于滤饼生长与井周压力分布的电阻率反演模型,反演钻井液侵入前后低渗气层的电阻率。
1 低渗气层钻井液侵入试验 1.1 试验装置及流程采用钻井液侵入动态模拟装置模拟钻井液循环过程中,钻井液滤液在钻井液液柱压力下通过滤饼进入储层的过程。
岩心的渗透率为0.73 mD,孔隙度为8.4%。钻井液的密度为1.3 kg/L,表观黏度为26 mPa·s,API滤失量为3.1 mL,固相粒度分布0.2~200.0 μm。试验条件为压差4 MPa,围压20 MPa,温度80 ℃。岩心尾端计量管的精度为0.02 mL。电极由前端向后依次排列,电极编号为R0、R1、R2和R3,电极间距为1.5 cm,使用电桥测量不同电极间的电阻率。
试验流程为:1) 将岩心放入夹持器;2) 先加较小围压,将钻井液加入模拟井筒,并加较小压力,然后将围压提至设定值,最后将钻井液压力增大至设定压力,以此为时间零点,并开始搅拌;3) 记录不同电极间的电阻率、岩心尾端计量管液面随时间的变化。
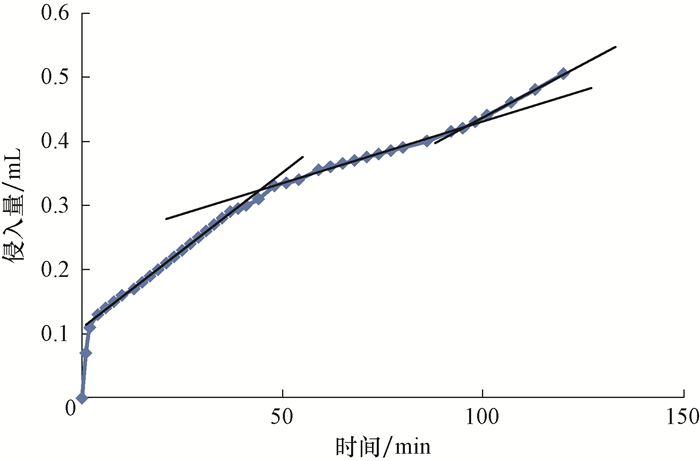
1.2 试验结果及分析根据岩心尾端计量管中液面变化,可获取不同时间下的钻井液滤液侵入量,并将其绘制成图(见图 1),以分析滤液侵入规律。从图 1可以看出:在前3 min内,钻井液滤液侵入量快速增大,为喷失阶段;在3~40 min阶段,钻井液滤液侵入量线性增长,侵入速率较大,为滤饼快速生长阶段;在40~80 min阶段,钻井液滤液侵入量线性增长,但侵入速率中等,为滤饼生长破坏平衡阶段;80 min以后,钻井液滤液侵入速率略大,原因是钻井液滤液完全侵入后,由气水两相流变成了液体单相流。
|
| 图 1 钻井液滤液侵入量与时间的关系 Fig.1 Correlation between drilling fluid invaded filtration volume and cumulative time |
根据侵入量变化特征,可将滤饼生长分为无滤饼阶段、滤饼快速生长阶段、滤饼生长破坏平衡阶段和滤饼形成封堵层阶段,其中滤饼形成封堵层阶段在试验过程中较少出现。一般认为滤饼承担大部分压降,可根据岩心尾端出水速率(图 1中的滤液侵入速率)、滤饼截面(5 cm2)、滤饼厚度(3 mm)、钻井液压力与岩心尾端压差(4 MPa),利用达西定律计算出滤饼快速生长阶段的滤饼渗透率为1.00 μD,滤饼生长破坏平衡阶段的滤饼渗透率为0.25 μD。
由于试验条件和地下地质条件的不同,需对试验测得的电阻率进行校正。根据温度对地层水电阻率的影响、围压对孔隙度的影响,对试验测得的电阻率进行校正。
地层水电阻率的校正系数为:
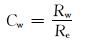
|
(1) |
式中:Cw为地层水电阻率校正系数;Rw为地层条件下的地层水电阻率,Ω·m;Re为试验条件下的地层水电阻率,Ω·m。
孔隙度的校正系数为:

|
(2) |
式中:Cp为孔隙度校正系数;φe为试验条件下的孔隙度;φt为地层条件下的孔隙度。
电阻率综合校正公式为:
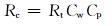
|
(3) |
式中:Rc为校正后的岩心电阻率,Ω·m;Rt为试验测得的电阻率,Ω·m。
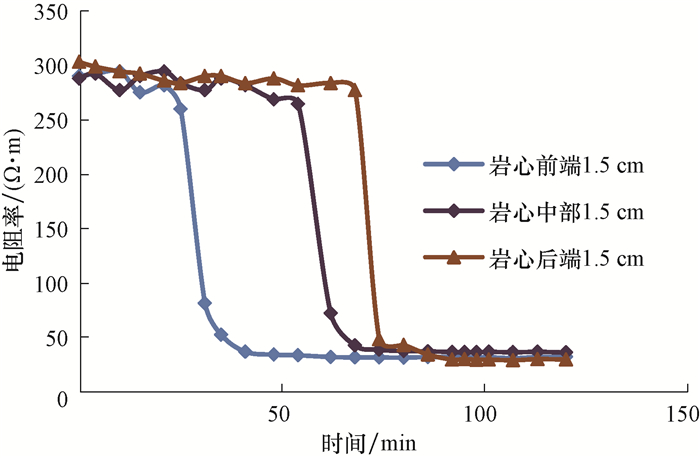
图 2为岩心不同位置在不同时间下校正后的电阻率。由图 2可知,钻井液滤液侵入会对岩心的电阻率造成影响,岩心不同位置的电阻率在80 min之后趋于稳定,这说明在80 min时钻井液滤液已完全侵入岩心。
|
| 图 2 岩心不同位置的电阻率随时间的变化 Fig.2 Changes in resistivity at different position of the core with cumulative time |
钻井液滤液侵入数值模拟采用平面径向一维模型[8],假设无外源,忽略重力和毛管力,根据达西定律、质量守恒定律、状态方程建立径向数值模拟的数学模型(初始条件为:pw|t=0=p0,Sw|t=0=Sw0;边界条件为:pw|rc=pref,pw|ra=p0):
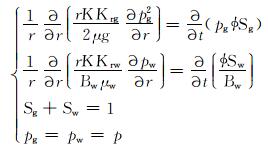
|
(4) |
式中:r为径向距离,m;K为绝对渗透率,mD;Krg和Krw分别为气相和水相的相对渗透率;μg和μw分别为气和水的黏度,mPa·s;pg和pw分别为气相和水相的压力,Pa;φ为孔隙度;Sg和Sw分别为气和水的饱和度;Bw为水相体积系数; pw|t=0为初始时刻水相的压力,MPa;Sw|t=0为初始时刻的含水饱和度;pw|rc为井壁处的水相压力,MPa;pw|ra为无穷远处的水相压力,MPa。
笔者利用Eclipse软件求解钻井液滤液侵入数学模型,并进行数值模拟。模拟时所需数据:1) 绝对渗透率、气相和水相的相对渗透率。2) 滤饼不同生长阶段的渗透率。根据钻井液侵入试验划分滤饼生长阶段,并计算滤饼的渗透率,滤饼快速生长阶段滤饼的渗透率为1.00 μD,滤饼生长破坏平衡阶段滤饼的渗透率为0.25 μD。3) 地层的孔隙度、渗透率。根据核磁测井曲线求得。4) 滤饼厚度。可根据钻头直径和井径测井曲线计算,如滤饼厚度大于3 mm,认为形成了封堵层;如井径扩径,说明井眼条件差,可认为滤饼质量差,不能形成封堵层。5) 地层压力和流体物性参数。6) 水相的地面密度取1.0 kg/L,压缩系数取5.0×10-4 MPa-1;岩石压缩系数取2.3×10-5 MPa-1;气体参考点处的黏度取0.017 mPa·s。
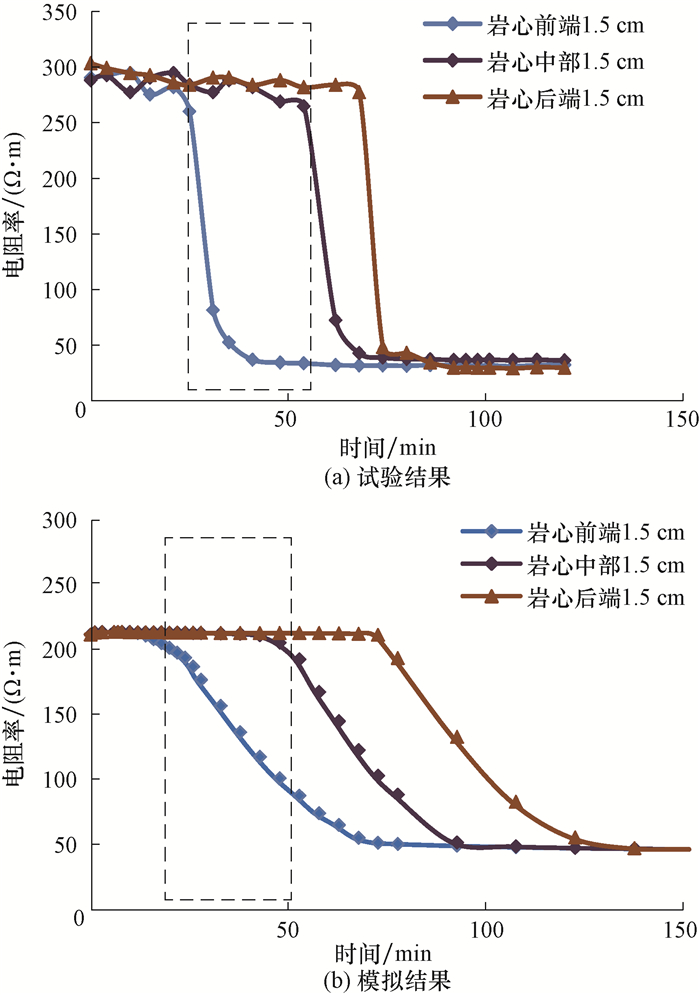
3 侵入试验结果与数值模拟正演结果对比通过对比侵入试验电阻率的变化与数值模型含水饱和度变化,检查数值模型孔隙度、渗透率的设定是否合理;通过对比测井电阻率与模型正演计算出的电阻率,检查数值模型的尺度是否合理。图 3为相同孔渗条件下的钻井液滤液侵入试验结果与数值模拟结果的对比,图中的黑虚线框为岩心前端1.5 cm处电阻率开始下降和岩心中部1.5 cm处电阻率开始下降的时间间隔。由图 3可知,数值正演模拟的岩心前端1.5 cm处电阻率开始下降和岩心中部1.5 cm处电阻率开始下降的时间间隔与侵入试验对应的时间间隔相同。因此,认为数值模型在孔隙度、渗透率等方面的设定符合实际情况。
|
| 图 3 相同孔渗条件下试验结果与数值模拟结果的对比 Fig.3 Comparison of experiment data and modeling data in same condition |
数值模拟的结果为网格化的含水饱和度随时间的变化曲线,进行处理时,将计算的不同时间、不同网格的含水饱和度导出,计算距井筒不同距离的平均含水饱和度。由于电阻率测井的电流环路近似于椭圆形,而数值模拟计算的又仅是某井深处一定半径范围内的平均含水饱和度,故电阻率测井的探测深度不能简单等同于数值模拟时的计算半径。笔者取径向积分几何因子0.8对应的径向深度(约3 m)作为计算平均含水饱和度的径向深度。表 1为依据半径3 m处的平均含水饱和度预测的钻井液滤液侵入后的电阻率与电缆测井的深电阻率。由表 1可知,数值模拟正演计算出的电阻率与电缆测井深电阻率比较接近,表明数值正演模型较为合理。
| 层位 | 顶深/m | 底深/m | 孔隙度,% | 渗透率/mD | 电阻率/(Ω·m) | |
| 实测 | 模拟 | |||||
| H4 | 3 774.00 | 3 779.00 | 7.1 | 0.35 | 42.0 | 40.4 |
| 3 779.00 | 3 789.00 | 9.1 | 6.79 | 19.3 | 17.5 | |
反演求取电阻率的思路是:1) 通过理论计算,获得钻井液侵入速率的计算公式;2) 根据钻井液侵入速率计算不同径向深度的平均含水饱和度;3) 根据含水饱和度计算电阻率随时间的变化,将其简化为电阻率反演公式;4) 根据测井深电阻率、浸泡时间及反演公式,计算时间零点的电阻率,并制作反演图版。
钻井液滤液侵入深度为re时,任一径向深度r处弧面的钻井液滤液通量qi为:
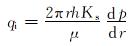
|
(5) |
式中:qi为任一径向深度r处弧面的钻井液滤液通量,m3;h为地层厚度,m;Ks为地层渗透率,mD;μ为钻井液滤液黏度,mPa·s;p为地层压力,MPa。
滤饼处的钻井液通量qc为:
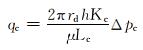
|
(6) |
式中:qc为滤饼处的钻井液通量,m3;rd为井筒半径,m;Kc为滤饼渗透率,mD;Lc为滤饼厚度,m;Δpc为滤饼两端的压差,MPa。
对式(5)进行整理,求积分得井周压力分布:

|
(7) |
将r=rd、p=pd和r=re、p=pe分别代入式(7)求得:
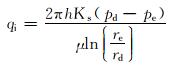
|
(8) |
式中:re为钻井液侵入径向深度,m;pe为原始地层压力,MPa;rd为井筒半径,m;pd为滤饼与地层接触面的压力,MPa。
由于滤饼处的滤液通量与地层任一径向深度r处弧面的滤液通量相等,因此联立式(6)和式(8)可得滤饼和地层中的压力分布:
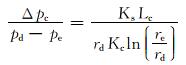
|
(9) |
根据式(9)获得的压力分布推导出钻井液滤液的侵入速率的计算公式为:
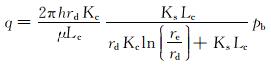
|
(10) |
式中:q为钻井液滤液的侵入速率,m3/s;pb为井筒压力与原始地层压力的压差,Pa。
由式(10)可知,对于滤饼渗透率、滤饼厚度、地层渗透率、井眼直径相同的层段,钻井液滤液的侵入速率仅与最大侵入深度re有关。上文的正演数值模拟显示在2~3 d后侵入深度达到2~3 m,侵入深度的变化较小,因此可以认为浸泡一段时间后,侵入深度不再增大,钻井液滤液的侵入速率也不再变化。
根据钻井液滤液侵入速率和地层孔隙度计算任一径向深度r处,t时刻的平均含水饱和度为:
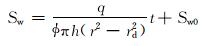
|
(11) |
式中:Sw为平均含水饱和度;Sw0为地层初始含水饱和度。
将式(11)代入阿尔奇公式得:
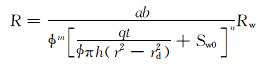
|
(12) |
式中:R为地层的电阻率,Ω·m;a,b,m和n为阿尔奇公式的参数。
式(12)为地层的电阻率和浸泡时间与初始含水饱和度之间的关系。
将式(12)中的Sw0消去,得电阻率反演公式:
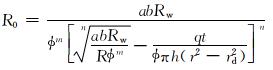
|
(13) |
式中:R0为反演的电阻率,Ω·m。
西湖凹陷某构造H4气层的阿尔奇公式参数a,b,m和n分别为0.94,1.00,1.81和1.99,地层水矿化度为10 000 mg/L。由西湖凹陷岩心的相对渗透率试验可知,西湖凹陷气藏的残余气饱和度约为15%,最大含水饱和度Sw为85%,气层的Sw0与气层的束缚水饱和度Swi相等。根据西湖凹陷XH-1井测井解释的渗透率、孔隙度等数据,利用式(13)反演该井H4气层的原状电阻率, 并根据反演结果计算对应的含水饱和度,结果见表 2。
| 顶深/m | 底深/m | 孔隙度,% | 渗透率/mD | 电阻率/(Ω·m) | 含水饱和度,% | |||
| 实测 | 反演 | 实测计算 | 反演计算 | |||||
| 3 774.00 | 3 779.00 | 7.1 | 0.35 | 42.0 | 75.6 | 56.0 | 44.4 | |
| 3 779.00 | 3 789.00 | 9.1 | 6.79 | 19.3 | 48.3 | 49.6 | 39.1 | |
| 3 806.00 | 3 848.00 | 6.7 | 0.61 | 30.6 | 53.5 | 50.1 | 37.5 | |
| 3 848.00 | 3 856.00 | 8.6 | 1.86 | 20.8 | 44.9 | 51.2 | 41.5 | |
| 3 856.00 | 3 873.00 | 5.6 | 0.25 | 45.5 | 81.7 | 50.4 | 43.2 | |
| 3 873.00 | 3 927.00 | 9.2 | 4.42 | 19.4 | 45.1 | 57.6 | 45.5 | |
由表 2可知,利用反演的电阻率计算的含水饱和度比用电缆测井的深电阻率计算的含水饱和度(简称测井解释含水饱和度)低7.0%~12.0%。对XH-1井H4气层进行测试,日产天然气达58×104 m3,无水产出。该井测井解释含水饱和度约为50.0%~60.0%,由相对渗透率试验获得的束缚水饱和度约45.0%~55.0%,若以测井解释含水饱和度为准,则该井可能产出少量水。而根据反演的地层原状电阻率计算的含水饱和度为40.0%~50.0%,更符合实际,证明反演出的电阻率与地层原状电阻率非常接近。
5 结论1) 低渗气层钻井液侵入试验结果表明,钻井液侵入过程分为无滤饼阶段、滤饼快速生长阶段、滤饼生长破坏平衡阶段和滤饼形成封堵层阶段等4个阶段,而滤饼形成封堵层阶段有时不会出现。
2) 对于滤饼渗透率、滤饼厚度、地层渗透率、井眼直径相同的层段,滤液侵入速率仅与最大侵入深度有关。
3) 钻井液滤液侵入会使地层电阻率降低,但随着侵入时间增长,地层电阻率降低幅度逐渐减小,侵入深度不再增大,地层电阻率不再降低。
4) 含水饱和度计算结果、相对渗透率试验和气井测试结果表明,反演出的钻井液滤液侵入前的电阻率与地层原状电阻率非常接近。
| [1] | MAKAROV A, ELTSOV I N.Invasion modeling assists in the formation permeability evaluation from resistivity profiles and mudcakethickness(Russian)[R].SPE 160584, 2012. |
| [2] | LING Kegang, ZHANG He, SHEN Zheng, et al.A comprehensive approach to estimate invasion radius of mud filtrate to evaluate formation damage caused by overbalanced drilling[R].SPE 168184, 2014. |
| [3] | 曹凤江, 肖光武. 钻井液粘度, 密度对气测全烃检测值影响的模拟实验[J]. 录井工程 , 2013, 24 (3) : 36–39. CAO Fengjiang, XIAO Guangwu. Simulation test for effect of drilling fluid viscosity, density on total hydrocarbon detection value of gas logging[J]. Mud Logging Engineering , 2013, 24 (3) : 36–39. |
| [4] | 常文会, 潘和平, 周峰. 泥浆侵入二维数值模拟[J]. 地球科学(中国地质大学学报) , 2010, 35 (4) : 674–680. CHANG Wenhui, PAN Heping, ZHOU Feng. Two-dimensional numerical simulation of mud invasion[J]. Earth Science(Journal of China University of Geosciences) , 2010, 35 (4) : 674–680. DOI:10.3799/dqkx.2010.082 |
| [5] | 刘尊年, 孙建孟, 迟秀荣, 等. 泥浆侵入研究现状分析[J]. 地球物理学进展 , 2012, 27 (6) : 2594–2601. LIU Zunnian, SUN Jianmeng, CHI Xiurong, et al. Analysis of research present situation of mud invasion[J]. Progress in Geophysics , 2012, 27 (6) : 2594–2601. |
| [6] | 范宜仁, 胡云云, 李虎, 等. 泥饼动态生长与泥浆侵入模拟研究[J]. 测井技术 , 2013, 37 (5) : 466–471. FAN Yiren, HU Yunyun, LI Hu, et al. Numerical simulation of mud-cake dynamic formation and reservoir mud filtrate invasion[J]. Well Logging Technology , 2013, 37 (5) : 466–471. |
| [7] | 丁娱娇, 邵维志, 王志勇, 等. 不同泥浆侵入环境下储层电性变化特征[J]. 测井技术 , 2009, 33 (4) : 315–320. DING Yujiao, SHAO Weizhi, WANG Zhiyong, et al. On the characteristics of formation resistivity variation under different mud invasion environments[J]. Well Logging Technology , 2009, 33 (4) : 315–320. |
| [8] | 张烈辉, 郭晶晶. 油气藏数值模拟基本原理[M]. 北京: 石油工业出版社 ,2014 . ZHANG Liehui, GUO Jingjing. Principle of reservoir numerical simulation[M]. Beijing: Petroleum Industry Press , 2014 . |




