2. 中国石油渤海钻探工程有限公司职工教育培训中心, 天津 300280
2. Staff Education and Training Center, CNPC Bohai Drilling Engineering Co. Ltd., Tianjin, 300280, China
在油气田钻井现场,普遍用马氏漏斗黏度计测定钻井液的漏斗黏度,以此作为快速评价和调控钻井液流变性的重要根据。尽管漏斗黏度受多种因素影响,但它能大体反映钻井液的流动性能。同时,表观黏度作为钻井液黏度的重要参数,已经成为衡量钻井液性能的常规指标。马氏漏斗黏度与表观黏度从不同角度反映了钻井液的流动特性,二者之间可能存在某种关系。国内外一些学者运用不同的方法对漏斗黏度与表观黏度的关系进行了研究[1-3]。
M.J.Pitt[1]最早研究马氏漏斗黏度与表观黏度的关系,基于能量守恒原理将钻井液设定为幂律流体,提出幂律模式是描述钻井液流变性的最佳模式[4-6],研究了不同流体的漏斗黏度和表观黏度,得到了表观黏度μ与漏斗黏度t以及流体密度ρ之间的数学关系式μ=ρ(t-25)。该式使用方便,但应用范围较小,钻井液表观黏度计算值与实测值误差较大,尤其是用于计算油基钻井液的表观黏度时相对误差达到了50%~75%。金业权[2]以室内试验结果为基础,测定并计算了一系列水基钻井液的漏斗黏度和表观黏度值,并通过曲线拟合得到两者之间的关系模型,但其适用于非牛顿流体,相对误差也比较大(为8%~23%),且没有从理论上揭示漏斗黏度和表观黏度的内在联系,试验数据也只涉及到水基钻井液。杨莉等人[3]基于漏斗黏度测定原理,探讨了钻井液在漏斗中流出的全过程,建立了马氏漏斗黏度和表观黏度之间的关系式。刘扣其等人[4]指出,当马氏漏斗形状一定时,钻井液在马氏漏斗中流动时受到的壁面剪切应力只取决于钻井液的密度,而与钻井液的类型无关。
笔者在上述研究成果的基础上,分析了油基钻井液在漏斗黏度计中的流动规律,建立了基于马氏漏斗黏度的油基钻井液表观黏度计算模型,并通过室内和现场试验验证了该模型的准确性。
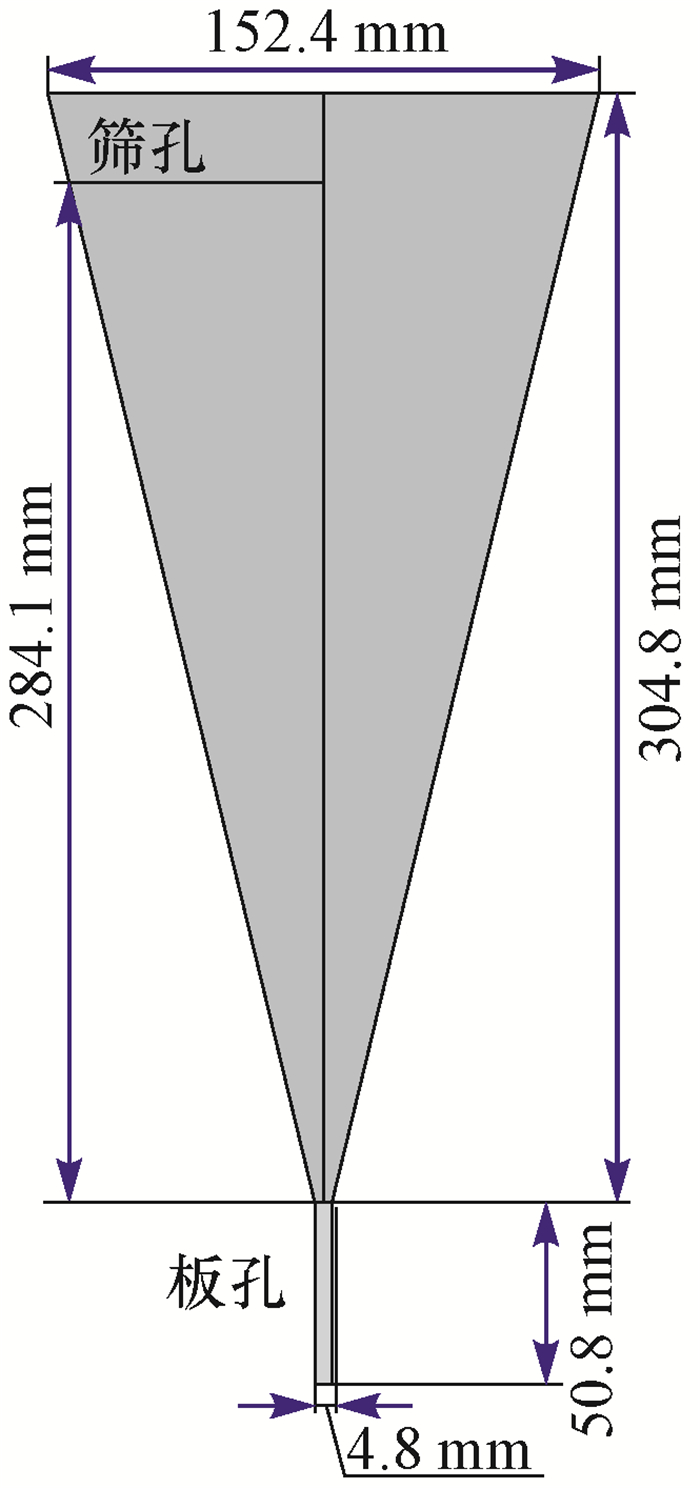
1 油基钻井液漏斗黏度计算方法 1.1 马氏漏斗黏度计结构特征马氏漏斗黏度计是API标准规定使用的一种测量钻井液黏度的仪器[7-8],其测量原理是在重力作用下使一定量(946 mL)的钻井液从一个固定型漏斗中自由流出,用该钻井液流完所需的时间来表示钻井液的黏度,单位通常用s表示[9]。马氏漏斗黏度计由锥体马氏漏斗、16目筛网和1 000 mL量杯组成,筛底以下的漏斗容积为1 500 mL,具体参数如图 1所示。
|
| 图 1 马氏漏斗结构尺寸 Fig.1 Dimensions of Marsh funnel |
国内外学者[10-11]研究了不同钻井液的流变性特征,并给出了所研究流体流变性的数学模型。流体在漏斗中流动,随着流体液面的变化,其剪切应力与剪切速率也在不断变化。在马氏漏斗锥体下口往上高度h处,其横截面面积可表示为:

|
(1) |
式中:A为马氏漏斗锥体下口往上h处的横截面面积,m2;r为马氏漏斗锥体下口往上h处的横截面半径,m;θ为马氏漏斗的半锥角, rad。
在dt时间内,从容器中流出了体积为dV的钻井液,液面下降了dh,则:
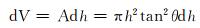
|
(2) |
式中:dt为时间变化量,s;dV为dt时间内的体积变化量,m3;dh为dt时间内流体液面高度的变化量,m。
设油基钻井液相对于理想流体的偏差系数为a,漏斗尺寸引起的偏差系数为b,漏斗的出流参数为c,则根据流体力学知识可知:
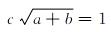
|
(3) |
设流体流速为v,由变水头流体出流特征可知:
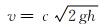
|
(4) |
利用积分学知识,在dt时间内漏斗中流出的钻井液体积dV可以表示为:
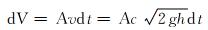
|
(5) |
结合式(2)与式(5)可得:
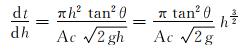
|
(6) |
将式(6)分离变量积分,可得:
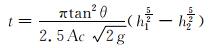
|
(7) |
式中:t为油基钻井液流体的漏斗黏度值,s;h1为开始测量漏斗黏度时的液面高度,m;h2为漏斗黏度测量后的液面高度,m;g为重力加速度,m/s2。
对于API标准的马式漏斗,在理想情况下,h1=28.405 cm,利用几何学知识求得h2=19.690 cm,且清水的马氏漏斗黏度为26 s。将以上数值代入式(7),可求得c=0.989 2,对于清水来说a=1。将a和c的值代入式(3),得b=0.022。由于b为漏斗尺寸引起的偏差系数,所以对于同一个漏斗,b值不变。
2 油基钻井液表观黏度预测模型的建立 2.1 预测油基钻井液表观黏度的可行性刘扣其等人[4]根据马氏漏斗中流体的受力平衡条件得到流体压降与流体剪切应力之间的关系,并结合流体力学相关知识得到如下关系式:
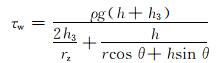
|
(8) |
式中:rz为马氏漏斗下端圆柱体的半径,m;h3为马氏漏斗下端圆柱体的高度,m;τw为流体在漏斗中流动时的剪切应力值,Pa;ρ为流体密度,kg/m3。
通过流体体积守恒原理和圆台体积公式求解h,得到流体液面高度与马氏漏斗结构的关系式:
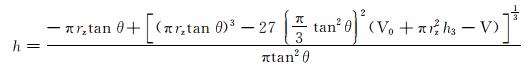
|
(9) |
式中:V0为马氏漏斗中流体的初始体积,mL; V为流出漏斗的流体体积,mL。
由式(9)可知,h受马氏漏斗结构特征的影响。若漏斗结构不变,在流出体积一定时,h为一定值。又由式(8)可知,若漏斗结构不变且h为一定值时,τw只与流体密度ρ有关。由此可以得出:当马氏漏斗形状一定时,钻井液在马氏漏斗中流动时受到的壁面剪切应力只取决于钻井液的密度,而与钻井液的类型无关。
因此,根据体积守恒定律,流体在漏斗黏度计中流动dt时间内的体积变化量dV一定,结合M.J.Pittt得到的漏斗黏度计算式,可推导并整理出油基钻井液表观黏度的预测公式。即从理论上讲,应用漏斗黏度预测油基钻井液表观黏度是可行的。
2.2 油基钻井液表观黏度计算公式M.J.Pitt[1]根据漏斗形状提出的模拟计算公式为:
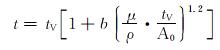
|
(10) |
式中:tV为体积为V的清水的马氏漏斗黏度,s;μ为所测流体的表观黏度,mPa·s;A0为喷嘴截面积,m2。
当室温为20 ℃时,tV=26 s,喷嘴处截面积A0=17.786 mm2。
代入式(10),得:

|
(11) |
则表观黏度的表达式为:
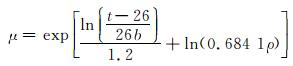
|
(12) |
将b=0.022代入式(12),最终得到预测油基钻井液表观黏度的公式为:
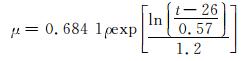
|
(13) |
在油田现场应用过程中,为了降低成本,常规油基钻井液都采用不同的油水比,形成油包水乳状液。油基钻井液中水的体积占总体积的体积分数称为含水量。
含水量的变化对油基钻井液表观黏度的影响如下:当含水量较低时,由于液滴数较少,液滴间的摩擦碰撞机会少,液滴相互作用小,而以流体力学的相互作用为主,故乳状液近似于牛顿流体;当含水量升高时,液滴数增多,液滴间的摩擦碰撞作用增强,相互作用力增大,乳状液变为非牛顿流体,而且含水量越高,非牛顿性越强[12];含水量继续升高,乳状液变成塑性流体,并出现屈服值,具有黏弹性。当含水量超过某一值时,表观黏度数值陡然下降,说明乳状液内部结构发生突变,即油包水乳状液可能发生了相反转[13],水成为连续相而转化为水包油乳状液。
在马氏漏斗中,含水量对油基钻井液表观黏度的影响受漏斗黏度的控制,由于漏斗黏度受多种因素影响,目前没有含水量与漏斗黏度的关系式。但这不妨碍探究含水量对所建立表观黏度预测模型准确性的影响,在模型验证部分,笔者将会进一步探讨。由于表观黏度预测公式本身具有一定的误差,故只用于粗略估算油基钻井液的表观黏度,如要得到精确的表观黏度数据,还需使用旋转黏度计测量。
3 模型验证 3.1 室内试验验证室内试验验证用全油基钻井液,为了在调节油基钻井液密度的同时获取合理的漏斗黏度和表观黏度值,对油基钻井液体系配方进行了优选,最终确定配方为:500 mL 5#白油+6 g主乳化剂+10 g辅助乳化剂+10 g润湿剂+10 g增黏剂+5 g氧化钙+10 g降滤失剂+10 g有机土+重晶石粉(作为加重剂调节密度)。通过调节加重剂的加量,配制出5种不同密度的油基钻井液,采用ZNN-D6型旋转黏度计测定其表观黏度,应用马氏漏斗测量其漏斗黏度,并利用式(13)计算其表观黏度预测值,结果见表 1。
| 试验编号 | 密度/ (kg·L-1) |
马氏漏斗 黏度/s |
表观黏度/(mPa·s) | 表观黏度相对误差,% | |
| 测定值 | 计算值 | ||||
| z-1 | 1.18 | 54 | 21.5 | 20.72 | 3.6 |
| z-2 | 1.30 | 55 | 22.5 | 23.51 | 4.5 |
| z-3 | 1.35 | 57 | 26.5 | 25.80 | 2.6 |
| z-4 | 1.40 | 58 | 29.5 | 27.48 | 6.8 |
| z-5 | 1.50 | 60 | 32.0 | 30.87 | 3.5 |
由表 1可知,在油基钻井液体系不变时,仅用加重剂改变钻井液的密度会造成漏斗黏度和表观黏度小幅上升;另外,通过式(13)计算得到的表观黏度值与实测表观黏度值的相对误差基本在5.0%以内,最大为6.8%,并且相对误差的大小并未随着钻井液体系密度的变化而出现大的波动。可见,笔者建立的数学模型对于不同密度的全油基钻井液表观黏度值的预测具有较高的准确性。
3.2 现场试验验证笔者利用阿尔及利亚地区多口井的油基钻井液现场实测数据,对建立的表观黏度预测模型进行了验证。这些井在采用油包水乳化钻井液钻进中,不断调整处理剂加量、提高钻井液密度和油水比,以保证钻井安全。其中,NGS-P-1井油基钻井液表观黏度的实测值和利用式(13)的计算值及其他相关数据见表 2。
| 井段/m | 密度/(kg·L-1) | 油水比 | 马氏漏斗黏度/s | 表观黏度/(mPa·s) | 表观黏度相对误差,% | |
| 实测值 | 计算值 | |||||
| 399.00~463.00 | 1.22 | 70:30 | 54 | 23.0 | 21.42 | 6.9 |
| 539.00~579.00 | 1.23 | 71:29 | 50 | 19.5 | 19.01 | 2.5 |
| 579.00~657.00 | 1.23 | 70:30 | 52 | 22.0 | 20.31 | 7.7 |
| 724.00~796.00 | 1.23 | 71:29 | 53 | 20.0 | 20.90 | 4.5 |
| 847.00~893.00 | 1.23 | 73:27 | 53 | 21.0 | 20.90 | 0.5 |
| 1 298.00~1 416.00 | 1.33 | 78:22 | 58 | 24.5 | 26.10 | 5.8 |
| 1 416.00~1 501.00 | 1.32 | 78:22 | 57 | 24.0 | 25.23 | 5.1 |
| 1 670.00~1 790.00 | 1.32 | 79:21 | 56 | 24.0 | 24.55 | 2.2 |
| 1 851.00~1 907.00 | 1.33 | 80:20 | 57 | 23.5 | 25.42 | 8.2 |
| 2 094.00~2 147.00 | 1.32 | 82:18 | 53 | 23.5 | 22.50 | 4.3 |
| 2 597.00~2 616.00 | 1.61 | 85:15 | 53 | 27.5 | 27.43 | 0.3 |
| 2 715.00~2 762.00 | 1.61 | 86:14 | 56 | 28.0 | 29.95 | 7.0 |
| 2 842.00~2 924.00 | 1.98 | 90:10 | 58 | 37.0 | 38.86 | 5.0 |
| 3 188.00~3 337.00 | 1.98 | 90:10 | 61 | 40.0 | 41.87 | 4.7 |
| 3 517.00~3 649.00 | 1.53 | 90:10 | 45 | 20.5 | 19.45 | 5.1 |
| 3 878.00~3 884.00 | 1.54 | 91:9 | 46 | 21.5 | 20.43 | 5.0 |
| 3 952.00~3 987.00 | 1.53 | 91:9 | 45 | 21.5 | 19.45 | 7.2 |
由表 2可知:油基钻井液表观黏度的实测值与计算值的相对误差一般在5.0%左右,最大为8.2%;随着钻井液密度和油水比不断增大,相对误差都保持在0.3%~8.2%,没有出现大的波动,这说明钻井液密度和油水比的改变并没有影响表观黏度预测模型的精确度。因此,该预测模型对于不同油水比的油基钻井液表观黏度的预测同样具有较高的准确性。
综上所述,式(13)对于油基钻井液表观黏度的预测具有较高的准确性,可以在油田现场推广应用。
4 结论1) 基于马氏漏斗黏度的测定原理,分析油基钻井液在马氏漏斗中的流动过程,建立了基于马氏漏斗黏度的油基钻井液表观黏度预测模型。室内和现场试验结果表明,该模型预测结果的相对误差在5.0%左右,最大为8.2%,并且适用于全油基钻井液和油包水乳化钻井液。
2) 油基钻井液含水量较低时,含水量和表观黏度基本呈线性关系,随着含水量升高表观黏度急剧增大,呈现出指数增长; 但含水量变化没有对预测模型的准确性造成影响。
3) 该模型的建立以前人的研究成果为基础,但对于预测油基钻井液表观黏度的准确度比前人所建模型要高,说明该模型在预测油基钻井液表观黏度方面具有更大的应用价值。
4) 作为一种预测模型,在油田现场应用可以快速预测油基钻井液的表观黏度值,但模型本身存在一定误差,如需精确的表观黏度数据,还需使用旋转黏度计测量。
| [1] | PITT M J. The Marsh funnel and drilling fluid viscosity:a new equation for field use[J]. SPE Drilling and Completion , 2000, 15 (1) : 3–6. DOI:10.2118/62020-PA |
| [2] | 金业权. 非牛顿流体漏斗黏度与塑性黏度的实验研究[J]. 西部探矿工程 , 2004, 16 (2) : 37–38. JIN Yequan. Experimental study of funnel viscosity and plastic viscosity of non-Newtonian fluid[J]. West-China Exploration Engineering , 2004, 16 (2) : 37–38. |
| [3] | 杨莉, 李家学, 刘会锋. 钻井液马氏漏斗黏度与表观黏度的关系[J]. 钻井液与完井液 , 2012, 29 (1) : 12–14. YANG Li, LI Jiaxue, LIU Huifeng. Study on the relationship between Marsh funnel viscosity and apparent viscosity of drilling fluids[J]. Drilling Fluid & Completion Fluid , 2012, 29 (1) : 12–14. |
| [4] | 刘扣其, 邱正松, 罗洋, 等. 应用马氏漏斗测定钻井液流变参数[J]. 钻井液与完井液 , 2014, 31 (5) : 60–62. LIU Kouqi, QIU Zhengsong, LUO Yang, et al. Measure rheology of drilling fluids with Marsh funnel viscometer[J]. Drilling Fluid & Completion Fluid , 2014, 31 (5) : 60–62. |
| [5] | 吕开河, 高锦屏, 孙明波. 多元醇钻井液高温流变性研究[J]. 石油钻探技术 , 2000, 28 (6) : 23–25. LYU Kaihe, GAO Jinping, SUN Mingbo. Study on high temperature rheological properties of polyol drilling fluid[J]. Petroleum Drilling Techniques , 2000, 28 (6) : 23–25. |
| [6] | 刘孝良, 刘崇建, 舒秋贵, 等. 应用漏斗黏度计测定幂律流体的流变参数[J]. 天然气工业 , 2003, 23 (4) : 47–50. LIU Xiaoliang, LIU Chongjian, SHU Qiugui, et al. Measuring rheological parameters of power law fluid by funnel viscometer[J]. Natural Gas Industry , 2003, 23 (4) : 47–50. |
| [7] | GURIA C, KUMAR R, MISHRA P. Rheological analysis of drilling fluid using Marsh Funnel[J]. Journal of Petroleum Science and Engineering , 2013, 105 : 62–69. DOI:10.1016/j.petrol.2013.03.027 |
| [8] | 汤凤林, 加里宁, 段隆臣, 等. 岩心钻探学[M]. 武汉: 中国地质大学出版社 ,2009 : 369 -370. DUAN Longchen, et al. Core drilling[M]. Wuhan: China University of Geosciences Press , 2009 : 369 -370. |
| [9] | 乌效鸣, 胡郁乐, 董红梅, 等. 钻井液与岩土工程浆液实验原理与方法[M]. 武汉: 中国地质大学出版社 ,2010 : 24 -25. WU Xiaoming, HU Yule, DONG Hongmei, et al. Experimental principle and method of drilling fluid and rock and soil engineering[M]. Wuhan: China University of Geosciences Press , 2010 : 24 -25. |
| [10] | 赵怀珍, 薛玉志, 李公让, 等. 抗高温水基钻井液超高温高压流变性研究[J]. 石油钻探技术 , 2009, 37 (1) : 5–9. ZHAO Huaizhen, XUE Yuzhi, LI Gongrang, et al. Rheological properties of high-temperature water based drilling fluids at high temperature and high pressure[J]. Petroleum Drilling Techniques , 2009, 37 (1) : 5–9. |
| [11] | 鄢捷年, 李志勇, 张金波. 深井油基钻井液在高温高压下表观黏度和密度的快速预测方法[J]. 石油钻探技术 , 2005, 33 (5) : 35–39. YAN Jienian, LI Zhiyong, ZHANG Jinbo. Methods for quickly predicting apparent viscosity and density of oil-based drilling fluids under HTHP conditions[J]. Petroleum Drilling Techniques , 2005, 33 (5) : 35–39. |
| [12] | 江延明, 李传宪. W/O乳状液的流变性研究[J]. 油气储运 , 2000, 19 (1) : 10–12. JIANG Yanming, LI Chuanxian. Research on rheologieal properties of W/O emulsion[J]. Oil & Gas Storage and Transportation , 2000, 19 (1) : 10–12. |
| [13] | 赵建兴. 对原油乳状液黏度变化规律的认识[J]. 油田地面工程 , 1985, 4 (4) : 15–21. ZHAO Jianxing. Some cognition on viscosity variation rule of crude emulsion[J]. Oil-Gas Field Surface Engineering , 1985, 4 (4) : 15–21. |


