2. 石油工程教育部重点实验室(中国石油大学(北京)), 北京 102249 ;
3. 中国石油大学胜利学院油气工程学院, 山东东营 257061
2. Key Laboratory for Petroleum Engineering of the Ministry of Education, China University of Petroleum(Beijing), Beijing, 102249, China ;
3. College of Petroleum Engineering, Shengli College, China University of Petroleum, Dongying, Shandong, 257061, China
为了提高老油田的采收率,一般需要在老井网的基础上钻加密调整井[1],老井网加密调整使井间距离变得更小,且老井的测斜数据不全或不准确,导致钻调整井时存在井眼碰撞风险。此外,在海上平台、人工岛密集丛式井及陆上丛式井的钻井过程中,同样面临着严重的井眼碰撞问题[2-3]。因此,井眼防碰技术已成为定向井、调整井安全作业的重点技术之一。目前,国外已经形成了一系列相对成熟的井眼防碰技术和探测工具,主要包括优化整体防碰设计方案、随钻测斜和防碰扫描计算、井眼轨迹控制技术等[4-6],同时比较成熟的主动探测工具主要有MGT电磁引导工具、RMRS旋转磁场测距导向系统、Wellspot目标井探测工具以及SWG单电缆引导工具,这些工具广泛应用于双水平井、连通井和丛式井等复杂结构井中。上述工具均存在一定局限:MGT和RMRS测量过程较繁琐而且费时,同时已钻井中下入的磁源或探管位置需要紧跟钻头进行移动,劳动强度大;Wellspot工具无法实现随钻测量,因此不适用于丛式井防碰;SWG是目前在丛式井钻井中最有效的防碰探测工具,克服了MGT和RMRS测量繁琐的问题,降低了劳动强度,也不需要提出钻具进行测量,但其需要在已钻井中下入电缆,特别当正钻井周围有多口已钻井可能相碰时,需要下入多根电缆,因而会影响已钻井的正常生产。同时,这些主动磁探测工具均需要在已钻井中下入设备,影响已钻井的生产。而且,目前这些国外产品的核心技术仍处于保密状态,无法了解具体的工作原理和测距导向算法[7-10]。
为了解决丛式井邻井井眼碰撞问题,保证丛式井安全、顺利钻进,笔者通过探讨丛式井随钻电磁测距防碰工具的工作原理及丛式井邻井间距计算方法,对丛式井邻井防碰进行了研究,以期为我国自主研发丛式井随钻电磁测距防碰工具提供理论支持。
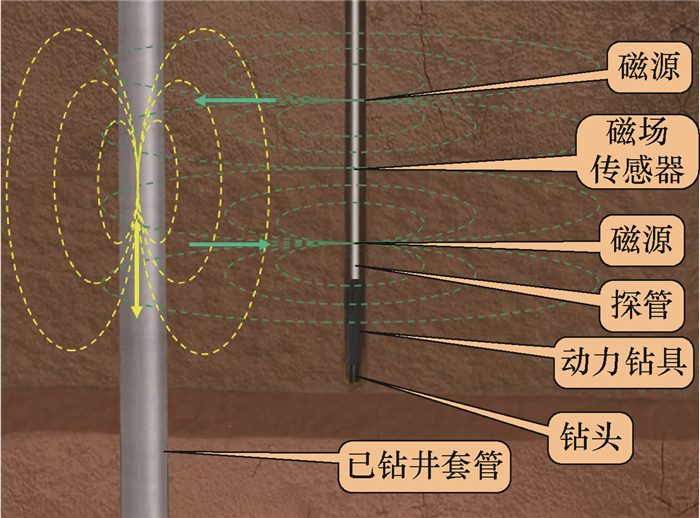
1 邻井随钻电磁测距防碰工具结构与原理为了实现丛式井实时测量邻井间距,防止邻井相碰,同时又不影响周边生产井的正常生产,在分析MGT电磁引导工具、RMRS旋转磁场测距导向系统、SWG单电缆引导工具等的优缺点后,笔者设计出一种新的邻井距离电磁探测工具——邻井随钻电磁测距防碰工具。该工具主要由磁源和探管组成,探管安装在井下动力钻具后面,磁源安装在探管外壳两端,磁场传感器安装在探管内部中间位置,2个磁源相对磁场传感器中心对称。
邻井随钻电磁测距防碰工具的基本原理如图 1所示。位于井下动力钻具后面的探管自身发出激励磁场,磁化邻井的套管,探管内部的磁场传感器探测到邻井套管被磁化后发出的新磁场的磁感应强度,结合探管自身姿态等数据,确定正钻井与邻井的相对距离和方位。
|
| 图 1 邻井随钻电磁测距防碰工具原理示意 Fig.1 Working principles of avoiding colliding with adjacent wells electromagnetic surveying while drilling tools |
2个磁源磁极互相平行,发出的磁场方向相反(见图 1中绿线)。当探管周围没有套管存在时,由于2个磁源发出的磁力线方向相反,如果2个磁源的磁场强度一致,则在磁场传感器位置处2个磁源发出的磁场互相抵消,合成磁场为0。当探管周围有套管存在时,在套管位置2个磁源发出的磁力线在套管轴线上的分量方向是相同的,因此套管将会被这个磁场磁化产生沿套管轴向的磁场(见图 1中黄线),该磁场被探管中间的磁场传感器探测到,进而得到相应的磁感应强度数据,然后通过丛式井邻井间距计算方法计算出正钻井与邻井之间的相对距离和方位,据此对正钻井井眼轨迹适当进行调整,以防止与邻井相碰。
2 丛式井邻井间距计算方法丛式井邻井间距计算方法是邻井随钻电磁测距防碰技术的核心,基于该算法使邻井随钻电磁测距防碰工具可以利用探管探测到的磁感应强度计算正钻井与邻井的间距和方位,从而实现丛式井邻井距离的随钻探测与控制。
2.1 磁源周围磁场分布规律邻井随钻电磁测距防碰工具的磁源长度一般为100~200 mm,直径为20~50 mm。在丛式井钻井中,邻井之间的距离应保持3 m以上,磁源尺寸远小于邻井间距离,因此可以将磁源看作是磁偶极子[11-13]。以磁偶极子中心为原点,z轴指向磁偶极子磁矩的方向,建立如图 2所示的直角坐标系和球坐标系。图 2中:P为空间任意一点,其球坐标为(r,θ,φ);r为P点到圆心O的距离,m;θ为PO与x轴的夹角,(°);φ为PO在xOy平面上的投影KO与y轴的夹角,(°)。在圆周上取任意点M,其坐标为(R,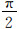

|
| 图 2 磁偶极子示意 Fig.2 Schematic diagram of magnetic dipole |
根据毕奥-萨伐尔定律,电流元Idl在空间点P处产生的磁感应强度dB为[14-15]:
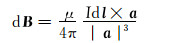
|
(1) |
式中:a为M点到P点的向量;dl为M点的切向量;μ为周围空间磁导率,(T·m)/A。
将a,dl用球坐标表示,代入式(1)后进行积分,
同时已知磁偶极子磁矩m=IS=πIR2,可得:
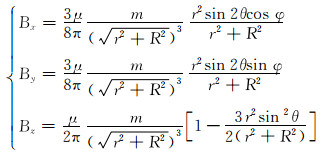
|
(2) |
式中:Bx,By,Bz分别为空间P点处的三轴磁感应强度分量,T;m为将磁源作为磁偶极子时的磁矩,A·m2。
丛式井随钻电磁测距防碰工具采集数据时,钻柱带动探管旋转,即磁偶极子绕y轴旋转。此时,邻井套管与磁偶极子的距离r可看作常数,φ=0,0≤θ≤2π,则:
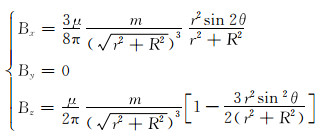
|
(3) |
因此:
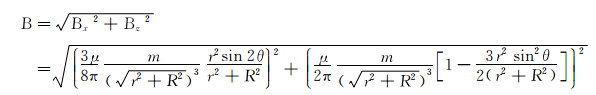
|
(4) |
由于套管到磁偶极子的距离远远大于磁源的半径,即r≫R,因此有:
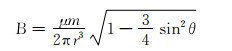
|
(5) |
在探管旋转过程中,磁源的轴向正对套管(即θ=0,π和2π)时,套管处有最大磁感应强度。利用这个最大磁感应强度,即可以判断邻井套管所在方向;而套管被磁化后磁感应强度的大小和探管与套管的距离有关,利用探测到的磁感应强度大小,即可计算出探管与套管的相对距离。
2.2 套管磁化磁场计算模型建立的套管磁化磁场计算模型如图 3所示。即以探管上部磁源中心为原点C,探管轴线为y轴,磁源轴线为z轴,建立直角坐标系。图 3中:探管中心到套管轴线的距离OE为d,m;套管轴线方向与探管轴线方向(y轴方向)的夹角为α,(°);探管两端的2个磁源之间的距离为2h,m;套管上任一点与磁源轴线的夹角为θ1,(°);套管上任一点与C点磁源的距离为r1,m;A点是C点的磁源轴线延长线与套管轴线AB的交点,B点是D点的磁源轴线延长线与套管轴线AB的交点。
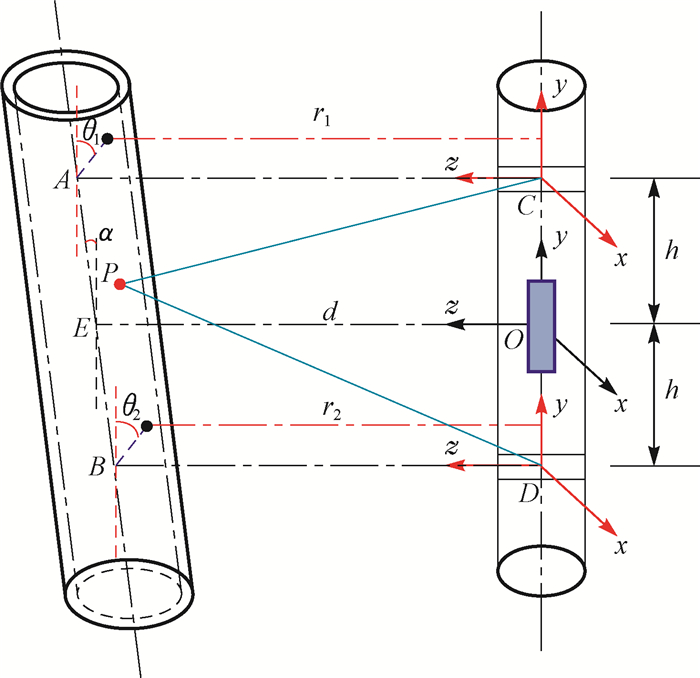
|
| 图 3 套管磁化磁场计算模型 Fig.3 Calculation model of magnetic intensity around casing |
提出以下假设条件:1)地层均匀各向同性;2)套管无限长且各向同性;3)套管半径远小于正钻井与邻井套管之间的距离;4)地层中无磁导率高的铁磁性矿物存在。利用式(5)即可计算邻井套管位置的磁感应强度。探测邻井距离过程中,由于r≫R,则根据式(2)可得C点的磁源周围的磁场分布为:

|
(6) |
式中:BCx,BCy和BCz分别为C点处的三轴磁感应强度分量,T。
磁源轴向正对套管时,磁场传感器探测到的磁感应强度最大,此时C点磁源轴向与套管所在平面的磁场分布为:
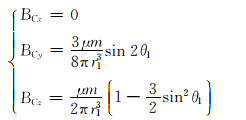
|
(7) |
在套管上任取一点,设套管的相对磁导率为μ1,则套管被C点磁源磁化后的磁场为:
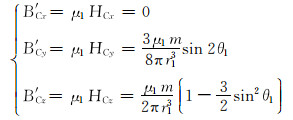
|
(8) |
同探管上部磁源一样,以探管下部磁源中心点为原点D,探管轴线为y轴,磁源轴线为z轴,建立直角坐标系。套管上任一点与磁源轴线的夹角为θ2,与D点磁源的距离为r2。D点的磁源与C点的磁源磁矩大小相等,磁极方向相反,套管被D点磁源磁化后的磁场为:

|
(9) |
在实际应用中,套管的总磁化磁场是2个磁源各自产生的磁化磁场之和。以磁场传感器所在的O点为原点,建立直角坐标系,P点为套管上任意一点(见图 3)。由式(8)、式(9)可知,套管被2个磁源磁化后的磁场并不是均匀分布的。为此,沿着套管轴线方向将套管均匀分割成若干微元,对于套管P点处的微元,其总磁化磁场为:
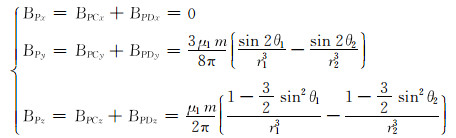
|
(10) |
设P点的直角坐标为P(x,y,z),由图 3可知,x=0,z=d+ytan α,将θ1,r1,θ2和r2用P点的直角坐标表示并代入式(10),可得P点的微元被2个磁源磁化后的磁感应强度为:
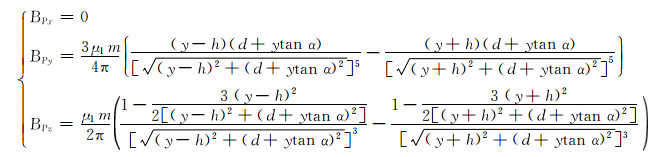
|
(11) |
套管被探管的2个磁源磁化后,其磁化磁场以y=0 m的位置为中心对称分布,磁场主要集中于中心附近区域,距离较远的位置磁感应强度很弱。
3 丛式井邻井距离计算磁场传感器位于探管中2个磁源的中点,磁场传感器探测到的磁场应包括地磁场、磁源的磁场和套管的磁化磁场。
对于C点磁源在磁场传感器位置产生的磁场,有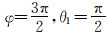
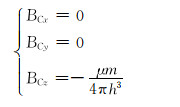
|
(12) |
同理,D点的磁源在磁场传感器位置产生的磁场为:
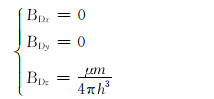
|
(13) |
由式(12)、式(13)可知, 2个磁源在磁场传感器位置产生的总磁场为0,因此磁场传感器感应到的磁场只剩下地磁场和套管的磁化磁场。地磁场在短时间内可以看作是恒定的,数据采集时可以直接减掉地磁场的数值,因此可以不考虑地磁场的影响。
与邻井间距d相比,P点的微元很小,因此可以将其看作磁偶极子。对于磁场传感器位置(即O点处),根据磁偶极子周围的磁场分布规律,可得:
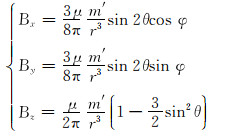
|
(14) |
式中:m′为将微元作为磁偶极子时的磁矩,A·m2。
当磁源正对套管时,P点的磁偶极子在磁场传感器处的磁感应强度为:
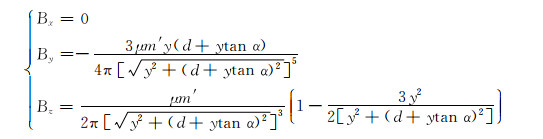
|
(15) |
已知磁偶极子的磁矩m′=VχmH,其中V为P点微元的体积,
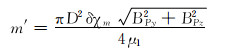
|
(16) |
计算过程中,首先应用式(11)计算P点的磁感应强度,然后依据式(16)计算磁偶极子的磁矩,再根据式(15)计算P点的磁偶极子在磁场传感器处的磁感应强度。
由于套管是一个很长的圆柱体,理论上套管上任意一点均会被磁化,因此磁场传感器感应到的总磁感应强度为:
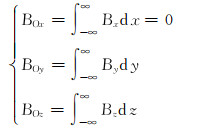
|
(17) |
由于磁场在地层传输过程中衰减很快,且邻井距离随钻测距防碰工具本身的测距范围约为10 m,y=10 m时磁场已衰减到纳特量级,经地层传输到磁场传感器位置后已衰减到皮特量级,对于磁场传感器来说已经无法分辨。因此仿真计算时,只取以磁场传感器为中心、±10 m的范围来计算。采用离散型数值计算方法,将±10 m的范围分成N等份,每等份长度为δ,计算每一点的磁感应强度为BPi,然后计算出每一点在磁场传感器位置产生的磁感应强度为BOi,最后计算总值,计算式为:
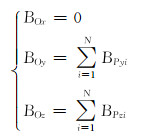
|
(18) |
由式(18)即可得到磁场传感器所探测到的总磁感应强度数值。
4 邻井随钻电磁测距影响因素根据邻井随钻电磁测距防碰计算方法,影响工具测量结果的因素主要包括探管内的磁源间距2h、磁源的磁矩m、套管的相对磁导率μ1、套管的直径c以及正钻井与邻井的夹角α。假设地层是均匀且各向同性的,周围地层中无铁磁性矿物的影响,分别分析各种影响因素对邻井随钻电磁测距防碰工具测量结果的影响。
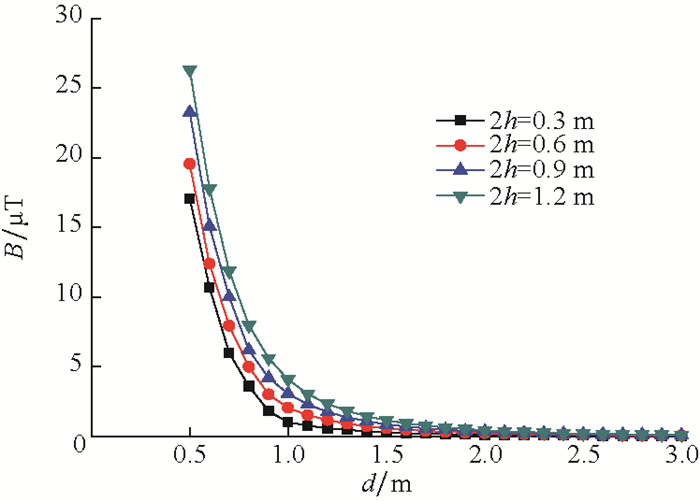
4.1 磁源对测量结果的影响磁源是邻井随钻电磁测距防碰工具的关键部件,其参数直接影响到工具的测量距离和测距精度。磁源影响测量精度的主要参数包括磁源间距和磁源磁矩。取μ0=4π×10-7H/m,μ1=1 000,α=0°,c=127.0 mm,m=10 A·m2,磁源间距取不同值时,对探管与套管之间距离0~3.0 m范围内的测量结果进行仿真,结果如图 4所示。
|
| 图 4 磁源间距对测量结果的影响 Fig.4 Effects of spacing between sources on measurement results |
由图 4可知,当磁源磁矩相同,而磁源间距为0.3 m时,探管探测到的磁感应强度较小;随着磁源间距增加,探管探测到的磁感应强度也在增加,但随着磁源间距增加,探管探测到的磁感应强度增加幅度很小,可以忽略。因此,在设计探管结构时,考虑探管自身的长度,磁源间距可设计为1.2 m,以使探管探测到的磁感应强度最大。
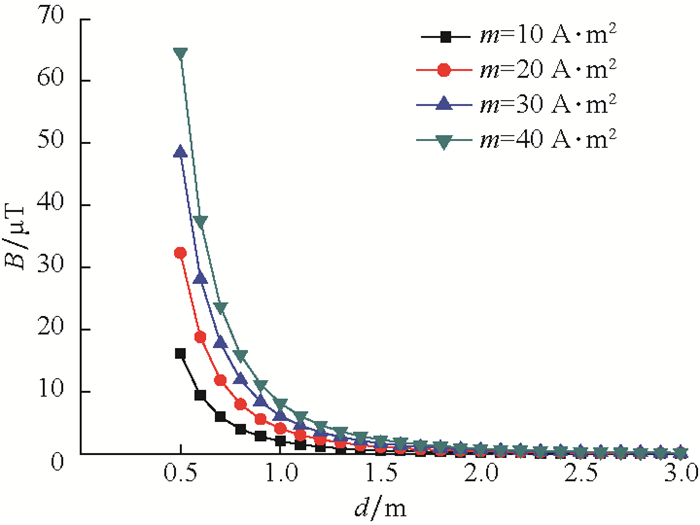
假设磁源间距2h=1.2 m,磁源磁矩取不同值时,对探管与套管之间的距离为0~3.0 m范围内的测量结果进行仿真,结果如图 5所示。
|
| 图 5 磁矩对测量结果的影响 Fig.5 Effect of magnetic moment on measurement results |
由图 5可知,当磁源间距固定时,磁源的磁矩越大,探管探测到的磁感应强度越大。因此,在设计探管结构时,应尽量选取磁矩大的磁源。笔者选用高磁矩的钕铁硼磁铁作为磁源,但永磁铁的磁矩受制于其体积,在空间狭小的井下无法安装大的永磁铁,而电磁信号源的磁矩由信号源的匝数和电流决定,随着电子技术尤其是超导材料和超级电容技术的进步,电磁信号源有很大发展前景,是电磁探测工具未来的发展方向。
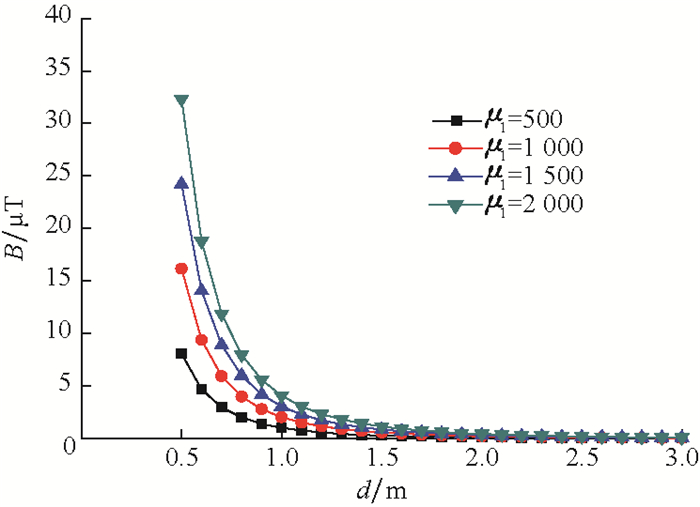
4.2 套管对测量结果的影响探管周围地层对探管内部磁源发出的磁场影响较小,但邻井中具有较高磁导率的套管会对磁源发出的磁场产生较大的影响。取m=10 A·m2,2h=1.2 m,α=0°,c=127.0 mm,套管的相对磁导率μ1取不同值时,对探管与套管之间的距离为0~3.0 m范围内的测量结果进行仿真,结果如图 6所示。
|
| 图 6 套管相对磁导率对测量结果的影响 Fig.6 Effect of relative magnetic conductivity of casing on measurement results |
由图 6可知,当磁源固定时,套管的相对磁导率越大,探管探测到的磁感应强度越大。套管的相对磁导率由套管自身的性质决定,不同套管的相对磁导率不同,因此计算邻井距离前,需要对邻井套管的相对磁导率进行测量,得到较准确的相对磁导率才能保证测量的精度。
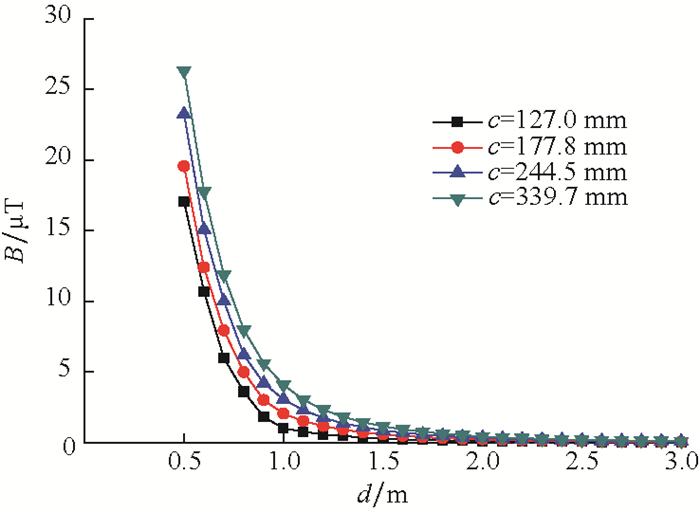
当套管的相对磁导率μ1=1 000时,取不同的套管直径,对探管与套管之间距离0~3 m范围内的测量结果进行仿真,结果如图 7所示。
|
| 图 7 套管直径对测量结果的影响 Fig.7 Effect of casing diameter on measurement results |
由图 7可知,当套管的相对磁导率固定时,套管的直径越大,探管探测到的磁感应强度越大。而在邻井间距相同的条件下,直径较大的套管碰撞的风险会增加,这也从另一方面证明了邻井随钻电磁测距防碰工具用于丛式井防碰的优越性。
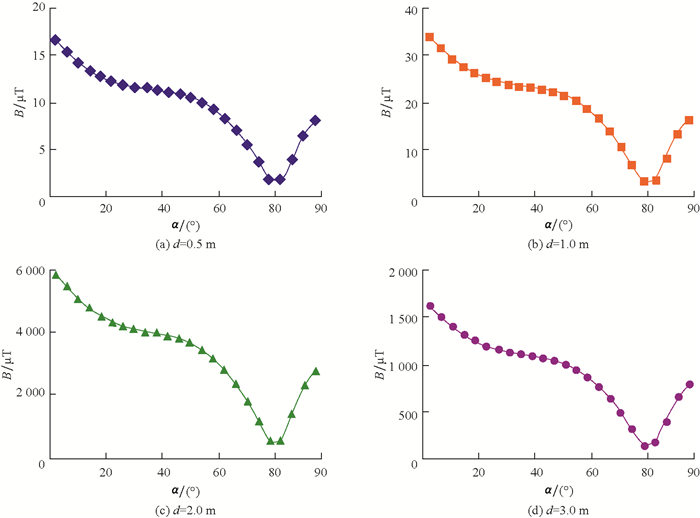
4.3 正钻井和邻井夹角对测量结果的影响在丛式井组中,正钻井与邻井会存在一定的夹角。由于该夹角的存在,探管两端的2个磁源与探管的距离不同,会对探管探测到的磁感应强度产生一定影响。假设2h=1.2 m,m=10 A·m2,μ1=1 000,c=127.0 mm,当正钻井和邻井夹角α在0°~90°变化时,对探管与套管之间的距离为0.5~3.0 m范围内的测量结果进行仿真,结果如图 8所示。
|
| 图 8 正钻井和邻井夹角对测量结果的影响 Fig.8 Effect of angle between drilling well and adjacent well on measurement results |
由图 8可知,以α=80°为拐点,探管探测到的磁感应强度变化趋势发生了突变。分析认为,这是因为当正钻井和邻井的夹角过大时,探管内距离套管较远的磁源在套管上产生的磁化磁场过小,磁源的磁极正对的方向也指向了套管的远处,相当于探管内只有一个磁源对套管产生了磁化作用,磁力线分布发生了变化,导致曲线发生突变。α从0°变化到50°左右时,探管探测到的磁感应强度基本降低为原来的一半,此时采集到的信号已经比较微弱。此外,α超过50°时,磁感应强度与夹角不再是对应关系。因此,在实际应用中,应避免在正钻井和邻井夹角超过50°时应用电磁测距防碰工具。对于过大的夹角,应更换其他测距工具进行测距,防止由于正钻井和已钻井夹角影响而导致数据偏差大,使邻井距离计算不准确而发生钻井故障。
5 结论与建议1) 将磁源看作磁偶极子,根据磁偶极子附近的磁场分布,通过推导套管被磁源磁化后的磁感应强度计算公式和磁场传感器探测到的磁感应强度计算公式,可以得到邻井随钻电磁测距防碰计算公式。根据磁场传感器探测到的磁感应强度,可以计算出邻井距离。
2) 设计探管时,应使探管内的磁源间距达到1.2 m以上;对于选用材料为永磁铁的磁源,应尽量选用较大体积的产品,以使磁源的磁矩更大,达到更远的测量距离和更高的测距精度。
3) 套管的相对磁导率越大,探管探测到的磁感应强度越大,对工具的测距精度越有利。计算邻井距离前,需要对邻井套管的相对磁导率进行测量,得到较准确的相对磁导率才能保证测量结果有足够的精度。邻井套管的直径越大,系统探测到的磁感应强度越大,对系统测距范围和精度越有利。
4) 在正钻井和邻井的夹角不超过50°的情况下,邻井随钻电磁测距防碰工具可以获得较准确的测量结果;超过50°时系统测距精度较低,需要换用其他探测工具进行测量,以防止发生钻井故障。
| [1] | 高德利. 复杂结构井优化设计与钻完井控制技术[M]. 东营: 中国石油大学出版社 ,2011 : 40 -67. GAO Deli. Optimized design and control techniques for drilling & completion of complex-structure wells[M]. Dongying: China University of Petroleum Press , 2011 : 40 -67. |
| [2] | 魏刚, 张春琳, 邵明仁. 小井距密集丛式定向井防碰技术[J]. 内蒙古石油化工 , 2010, 36 (2) : 99–101. WEI Gang, ZHANG Chunlin, SHAO Mingren. Anti-collision technology of short-distance directional cluster well[J]. Inner Mongolia Petrochemical Industry , 2010, 36 (2) : 99–101. |
| [3] | POEDJONO B, CONRAN G, AKINNIRANYE G, et al.Minimizing the risk of well collisions in land and offshore drilling[R].SPE 108279, 2007. http://www.onepetro.org/mslib/app/Preview.do?paperNumber=SPE-108279-MS |
| [4] | 张凤久, 罗宪波, 刘英宪, 等. 海上油田丛式井网整体加密调整技术研究[J]. 中国工程科学 , 2011, 13 (5) : 34–40. ZHANG Fengjiu, LUO Xianbo, LIU Yingxian, et al. Research on overall encryption adjustment technology of offshore oil field[J]. Engineering Science , 2011, 13 (5) : 34–40. |
| [5] | POEDJONO B, PHILLIPS J W, LOMBARDO G.Anti-collision risk management stanard for well placement[R].SPE 121040, 2009. http://www.onepetro.org/download/conference-paper/SPE-121040-MS?id=conference-paper/SPE-121040-MS |
| [6] | POEDJONO B, ISEVCAN E, LOMBARDO G J, et al.Anti-collision and risk management offshore Qatar:a successful collaboration[R].IPTC 13142, 2009. |
| [7] | 刁斌斌.邻井距离随钻电磁探测与扫描监测计算方法研究[D].北京:中国石油大学(北京), 2012. DIAO Binbin.Research on calculation methods for scanning monitoring & electromagnetic detection of adjacent well distance while drilling[D].Beijing:China University of Petroleum (Beijing), 2012. |
| [8] | 刁斌斌, 高德利. 邻井定向分离系数计算方法[J]. 石油钻探技术 , 2012, 40 (1) : 22–27. DIAO Binbin, GAO Deli. Calculation method of adjacent well oriented separation factors[J]. Petroleum Drilling Techniques , 2012, 40 (1) : 22–27. |
| [9] | GRILLS T L.Magnetic ranging technologies for drilling steam assisted gravity drainage well pairs and unique well geometries:a comparison of technologies[R].SPE 79005, 2002. |
| [10] | 王德桂, 高德利. 管柱形磁源空间磁场矢量引导系统研究[J]. 石油学报 , 2008, 29 (4) : 608–611. WANG Degui, GAO Deli. Study of magnetic vector guide system in tubular magnet source space[J]. Acta Petrolei Sinica , 2008, 29 (4) : 608–611. |
| [11] | 李翠, 高德利. 救援井与事故井连通探测方法初步研究[J]. 石油钻探技术 , 2013, 41 (3) : 56–61. LI Cui, GAO Deli. Preliminary research on detection method for connecting relief well to blowout well[J]. Petroleum Drilling Techniques , 2013, 41 (3) : 56–61. |
| [12] | 席宝滨, 高德利. U形水平井连通过程中的相对位置不确定性分析[J]. 石油钻探技术 , 2014, 42 (6) : 18–24. XI Baobin, GAO Deli. Analysis of the relative position uncertainty in the intersecting process of U-shaped horizontal wells[J]. Petroleum Drilling Techniques , 2014, 42 (6) : 18–24. |
| [13] | 唐劲飞, 龚沈光, 王金根. 基于磁偶极子模型的目标定位和参数估计[J]. 电子学报 , 2002, 30 (4) : 614–616. TANG Jinfei, GONG Shenguang, WANG Jingen. Target positioning and parameter estimation based on magnetic dipole model[J]. Acta Electronica Sinica , 2002, 30 (4) : 614–616. |
| [14] | 张玉民, 戚伯云. 电磁学[M]. 北京: 科学出版社 ,2000 : 79 -96. ZHANG Yumin, QI Boyun. Electromagnetics[M]. Beijing: Science Press , 2000 : 79 -96. |
| [15] | 陈小斌, 赵国泽. 关于人工源极低频电磁波发射源的讨论:均匀空间交流点电流源的解[J]. 地球物理学报 , 2009, 52 (8) : 2158–2164. CHEN Xiaobin, ZHAO Guoze. Study on the transmitting mechanism of CSELF waves:response of the alternating current point source in the uniform space[J]. Chinese Journal of Geophysics , 2009, 52 (8) : 2158–2164. |


