为避免井下故障、提高钻井效率而逐步发展形成的聚合物钻井液体系已成为当今钻井完井过程中常用的钻井液类型之一,但聚合物在孔隙喉道中的吸附滞留会造成储层渗透率下降及润湿性改变,从而造成储层伤害[1]。聚合物对储层的伤害可以分为2种:一种是聚合物由于力的作用在多孔介质中的滞留;另一种是聚合物在多孔介质中的吸附。第一种伤害可以通过流体的反排,在一定程度上予以解除,是可逆的;而第二种伤害则是不可逆的[2]。聚合物在储层中的吸附可分为层吸附和桥吸附:当聚合物的链长小于孔隙直径或携带液的流速小于聚合物发生剪切伸长的临界流速时,聚合物在孔隙表面的吸附为层吸附;当携带液的流速大于聚合物发生剪切伸长的临界流速且聚合物发生剪切伸长后的长度大于孔隙直径时,部分聚合物分子横跨孔隙发生的吸附为桥吸附[3]。
Necmettin Mungan[4]通过岩心试验研究了溶液盐度、剪切速率和聚合物浓度对聚合物在岩心中吸附的影响。Cohen Yoram等[5]根据表面过程原理设计了一种试验方法,通过驱替试验研究聚合物在岩石孔隙中的吸附和滞留对孔隙介质流动性的影响。A.Zaitoun等[6]利用人造岩心研究了储层的非均质性和残余油对聚合物吸附的影响。在聚合物用于油井调剖时,P.L.J.Zitha等[7]在考虑聚合物分子之间排斥力与吸引力对聚合物吸附影响的基础上,建立了聚合物的吸附数学模型。A.Zaitoun等[8]利用人造岩心与天然岩心进行了聚合物驱替试验,研究了流速、非均质性、聚合物类型对聚合物吸附的影响。P.L.J.Zitha等[9]根据聚合物或凝胶在多孔介质中的吸附机理,在考虑聚合物或凝胶层吸附或桥吸附的基础上,利用毛细管模型构建了聚合物在多孔介质中吸附的数学模型,并对聚合物和凝胶在调剖堵水过程中的堵水效果及影响因素进行了分析。A.L.Ogunberu等[10]通过试验,研究了聚合物在多孔介质中的吸附机理,指出聚合物对多相流的各相相渗透率有较大影响。
笔者在充分调研国内外聚合物伤害模拟评价技术的基础上,建立了低渗储层近井地带聚合物伤害模型,给出了可由计算机迭代求解的差分方程组,并利用所建立的模型,对钻井过程中影响聚合物伤害的主要因素进行了定性分析。
1 聚合物伤害模型的建立常规的室内评价试验可为储层伤害评价与防治提供可信的第一手资料,但费时费力,且无法准确给出储层伤害的深度与程度。为研究低渗储层近井地带的聚合物伤害,建立井筒条件下储层伤害的数学模型,首先做了以下假设:1)低渗储层为均质油藏;2)流动过程为等温流动;3)忽略重力对流体流动的影响;4)储层中流体的流动为油水两相流。
根据聚合物在岩心中的质量守恒及Langmuir吸附定律,建立地层条件下的聚合物伤害数学模型。
根据质量守恒,油水两相的连续性方程为:
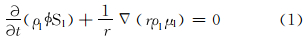
式中:ρ1为液体密度,g/cm3;φ为地层孔隙度;Sl为含水饱和度;r为流动半径,cm;μl为液体黏度,mPa·s。
聚合物在孔隙介质中流动时,根据质量守恒,聚合物的质量浓度可表示为:
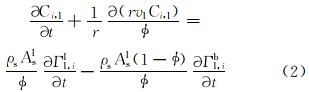
式中:Ci,l为聚合物质量浓度,g/cm3;t为接触时间,h;vl为液体流动速度,m/h;Asl为单位质量岩石骨架中能发生层吸附的孔隙表面积,m2/g;Гl为岩石骨架单位表面积上的层吸附量,g/m2;Гb为岩石骨架单位表面积上的桥吸附量,g/m2;上角标l指层吸附,b指桥吸附;下角标i表示溶液中聚合物的种数。
桥吸附概率连续性方程为:

式中:Cl,i,o为聚合物桥吸附质量浓度,g/cm3;P为能在孔隙中发生桥吸附的聚合物质量分数,%;ζ为常数。
层吸附速率:
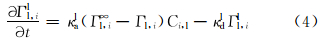
式中:κal为总的层吸附速率,cm3/(g·h);κdl为层吸附聚合物层脱附速率,cm3/h;Гl∞为岩石骨架单位表面积上的最大层吸附量,g/cm2。
桥吸附速率:
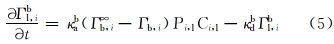
式中:κab为总的桥吸附速率,cm3/(g·h);κdb为桥吸附聚合物脱附速率,cm3/h。
根据文献[11]的研究结果,利用室内模拟评价试验数据拟合得到了层吸附速率、层吸附聚合物脱附速率与聚合物质量浓度的关系式:

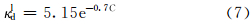
吸附平衡时的层吸附量:
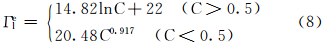

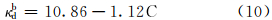
吸附平衡时的桥吸附量:

根据文献调研[11],在单因素聚合物伤害过程中,聚合物的吸附量与渗透率之间存在一定的关系,若发生桥吸附的孔道分数为f,渗透率与吸附量之间的表达式可写为:
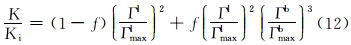
式中:K为伤害后的渗透率,mD;Ki为初始渗透率,mD;Гmaxl为岩石骨架单位表面积上的最大层吸附量,g/cm2;Гmaxb为岩石骨架单位表面积上的最大桥吸附量,g/cm2。
储层发生伤害后,渗透率下降,导致流动阻力增加,可用表皮系数表示增加的流动阻力,其表达式为:
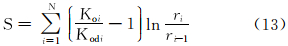
式中:Koi为第i个网格的原始渗透率,mD;Kodi为第i个网格伤害后的渗透率,mD;ri为第i个网格到井的半径,m;ri-1为第i-1个网格到井的半径,m;N为伤害区域划分的网格数。
2 聚合物伤害模型的求解对所建立的模型进行数值求解,需要将数学模型在空间和时间上进行离散,然后对离散系统进行线性化,得到线性方程组,以求解线性代数方程组代替求解偏微分方程组。
利用IMPES方法对聚合物质量守恒方程进行显示差分,可以得到其差分方程为:
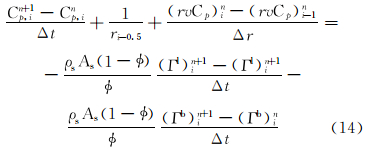
桥吸附的差分方程为:

层吸附速率的差分方程为:
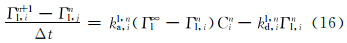
桥吸附速率的差分方程为:
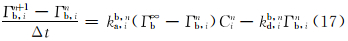
由此,即可由计算机迭代求解出聚合物伤害引起的渗透率降低率和不同深度下的聚合物吸附量。
3 聚合物伤害模型的应用根据前述分析,聚合物伤害主要是由于聚合物的层吸附和桥吸附引起的。采用如下参数分析影响聚合物伤害的因素:井眼半径rw=9.52 cm;地层渗透率为Kd=10 mD;地层孔隙度φ=15.5%;流动外边界re=1 000 cm;工作液密度为ρf=1.2 g/cm3,工作液黏度μf=2.2 mPa·s;地层原油黏度为μf=2.5 mPa·s;聚合物延伸临界速率为τc=70 s-1;单位孔隙表面积上的最大层吸附量为0.57 g/m2;聚合物单位孔隙表面积上的最大桥吸附量为0.17 g/m2;单位质量岩石颗粒的表面积为1.9 m2/g。
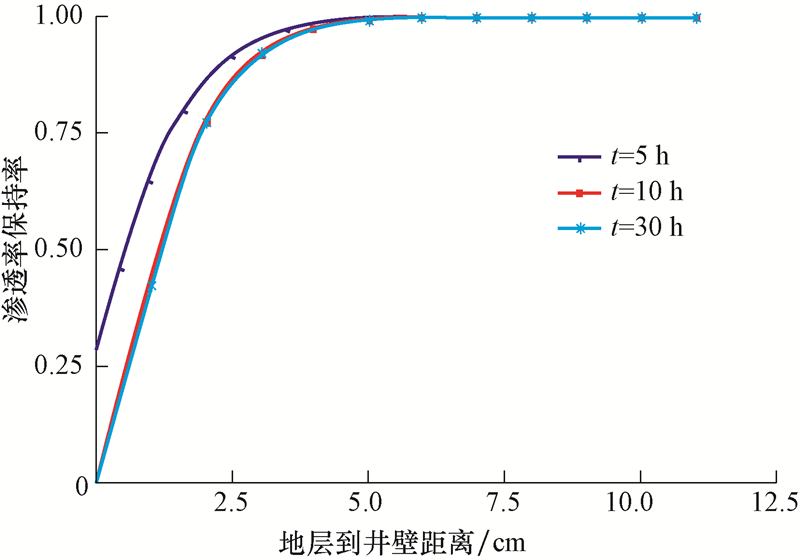
3.1 接触时间对聚合物伤害的影响当地层渗透率Ki=10 mD,钻井液液柱压力与井底压力之间的差值Δp=5 MPa,聚合物质量浓度C=0.1 g/cm3时,计算不同接触时间下,渗透率保持率和聚合物吸附量与地层到井壁之间距离的关系,结果如图 1和图 2所示。
|
| 图1 不同接触时间下,渗透率保持率与地层到井壁之间距离的关系 Fig.1 The relationship between permeability retention rate and the distance from the formation to the borehole wall at different contact times |

|
| 图 2 不同接触时间下,聚合物吸附量与地层到井壁之间距离的关系 Fig.2 The relationship between polymer adsorption and the distance from the formation to the borehole wall at different contact times |
由图 1和图 2可知,随着接触时间增长,聚合物吸附量增大,渗透率保持率下降,初始聚合物的吸附
速率最快,随着聚合物吸附量增大,聚合物吸附速率逐渐降至0。这是由于聚合物在岩石表面的吸附符合Langmuir等温吸附定律,随着岩石表面吸附聚合物量增加,聚合物在岩石表面的吸附逐渐达到平衡,因而吸附速率下降。
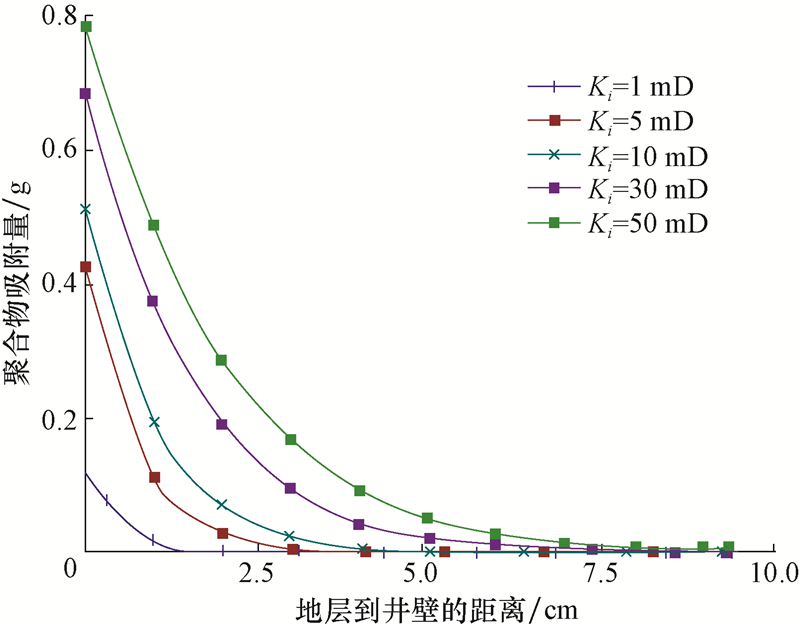
3.2 地层渗透率对聚合物伤害的影响当接触时间t=15 h,钻井液液柱压力与井底压力之间的差值Δp=5 MPa,聚合物浓度C=0.1 g/cm3时,计算不同地层渗透率下,渗透率保持率和聚合物吸附量与地层到井壁之间距离的关系,结果如图 3和图 4所示。

|
| 图 3 不同渗透率下,渗透率保持率与地层到井壁之间距离的关系 Fig.3 The relationship between permeability retention rate and the distance from the formation to the borehole wall at different permeability |
|
| 图 4 不同渗透率下,聚合物吸附量与地层到井壁之间距离的关系 Fig.4 The relationship between polymer adsorption and the distance from the formation to the borehole wall at different permeability |
由图 3和图 4可知,随着地层渗透率增大,聚合物在地层中的吸附量升高,渗透率保持率降低。这是由于随着地层渗透率增大,钻井液滤失时的流动
阻力减小,滤失速度增大,聚合物侵入地层的速度和质量增加,因而地层中聚合物吸附量升高,渗透率保持率降低。
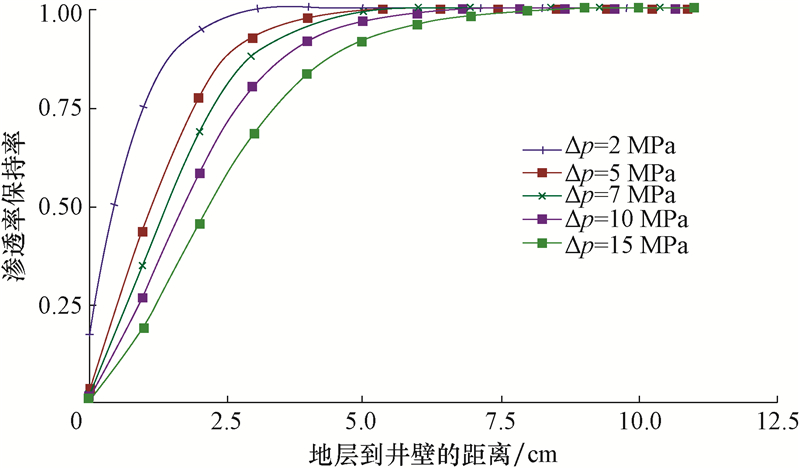
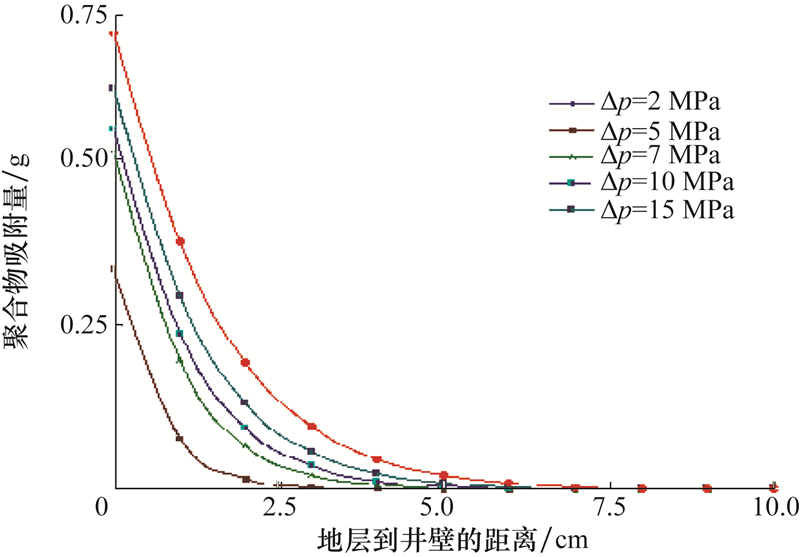
3.3 压差对聚合物伤害的影响当接触时间t=15 h,地层渗透率Ki=10 mD,聚合物浓度C=0.1 g/cm3时,计算不同钻井液液柱压力与井底压力之间差值下,渗透率保持率和聚合物颗吸附量与地层到井壁之间距离的关系,如图 5和图 6所示。
|
| 图 5 不同压差下,渗透率保持率与地层到井壁之间距离的关系 Fig.5 The relationship between permeability retention rate and the distance from the formation to the borehole wall at different differential pressures |
|
| 图 6 不同压差下,聚合物吸附量与地层到井壁之间距离的关系 Fig.6 The relationship between polymer adsorption and the distance from the formation to the borehole wall at different differential pressures |
由图 5和图 6可知,随着钻井液液柱压力与井底压力差值的增大,聚合物在地层中的吸附量升高,渗透率保持率降低。这是由于随着钻井液液柱压力与井底压力差值增大,钻井液滤失速度增大,聚合物侵入地层的速度和质量增加,因而地层中聚合物吸附量升高,渗透率保持率降低。
3.4 聚合物质量浓度对聚合物伤害的影响当接触时间t=15 h,地层渗透率Ki=10 mD,钻井液液柱压力与井底压力之间差值Δp=5 MPa时,计算不同聚合物质量浓度下,渗透率保持率和聚合物吸附量与地层到井壁之间距离的关系,结果如图 7和图 8所示。

|
| 图 7 不同聚合物质量浓度下,渗透率保持率与地层到井壁之间距离的关系 Fig.7 The relationship between permeability retention rate and the distance from the formation to the borehole wall at different polymer mass concentrations |

|
| 图 8 不同聚合物质量浓度下,聚合物吸附量与地层到井壁之间距离的关系 Fig.8 The relationship between polymer adsorption and the distance from the formation and to borehole wall at different polymer mass concentrations |
由图 7和图 8可知:随着聚合物质量浓度增大,近井地带聚合物吸附量升高,渗透率保持率降低,聚合物伤害深度变浅。分析认为在高聚合物质量浓度下,聚合物在近井地带快速吸附,增加了钻井液滤失时的阻力,降低了钻井液的滤失速率,从而阻止聚合物进一步进入地层。
3.5 毛管力对聚合物伤害的影响当接触时间t=15 h,地层渗透率Ki=10 mD,
钻井液液柱压力与井底压力之间的差值Δp=5 MPa,聚合物浓度C=0.1 g/cm3时,计算不同初始饱和度毛管压力下,渗透率保持率和聚合物吸附量与地层到井壁之间距离的关系,结果如图 9和图 10所示。

|
| 图 9 不同毛管压力下,渗透率保持率与地层到井壁之间距离的关系 Fig.9 The relationship between permeability retention rate and the distance from the formation to the borehole wall at different capillary forces |

|
| 图 10 不同毛管压力下,聚合物吸附量与地层到井壁之间距离的关系 Fig.10 The relationship between polymer adsorption and the distance from the formation to the borehole wall at different capillary forces |
由图 9和图 10可知,在不同毛管压力下,聚合物吸附量曲线和渗透率保持率曲线几乎重合,毛管力对内滤饼的形成影响较小。
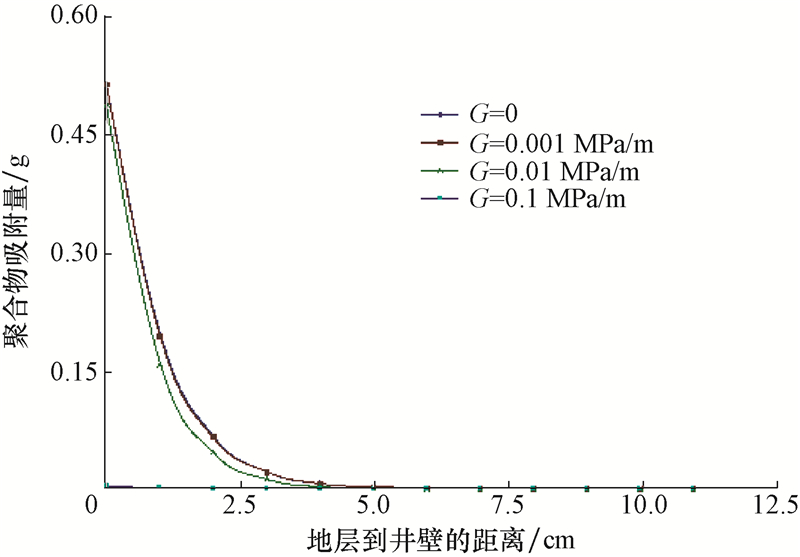
3.6 启动压力梯度对聚合物伤害的影响当接触时间t=15 h,地层渗透率Ki=10 mD,钻井液液柱压力与井底压力之间的差值Δp=5 MPa,聚合物浓度C=0.1 g/cm3时,计算不同启动压力梯度下,渗透率保持率和聚合物吸附量与地层到井壁之间距离的关系,结果如图 11和图 12所示。

|
| 图 11 不同启动压力梯度下,渗透率保持率与地层到井壁之间距离的关系 Fig.11 The relationship between permeability retention rate and the distance from the formation to the borehole wall at different starting pressure gradients |
|
| 图 12 不同启动压力梯度下,聚合物吸附量与地层到井壁之间距离的关系 Fig.12 The relationship between polymer adsorption and the distance from the formation to the borehole wall at different starting pressure gradients |
由图 11和图 12知:由于研究的流动半径较小,当启动压力梯度较小(<0.01 MPa/m)时,启动压力产生的总阻力较小,因而启动压力梯度对渗透率保持率和聚合物吸附量的影响不大;当启动压力梯度较大时,在研究半径内,启动压力梯度的存在造成了较大的流动阻力,严重时甚至导致流体不流动,在这种条件下启动压力梯度可降低聚合物伤害。
4 结 论1) 聚合物伤害主要发生在近井壁地带,当地层渗透率较低时,聚合物伤害的程度和深度均相对较小。
2) 随着钻井液液柱压力与井底压力压差的增大,聚合物伤害的程度和深度均增大。
3) 随着聚合物质量浓度变大时,其伤害半径和伤害程度均有所降低。
4) 启动压力梯度可在一定范围内降低聚合物对储层的伤害程度。
| [1] |
向兴金,蒋发太,赵霞,等.聚合物钻井液对储层损害因素的研究[J].钻井液与完井液,1996,13(1):40-41. Xiang Xingjin,Jiang Fatai,Zhao Xia,et al.Study of reservoir damage factors of polymer drilling fluid[J].Drilling Fluid & Completion Fluid,1996,13(1):40-41. |
| [2] |
李云波,乌效鸣,蔡记华.运用生物酶降低聚合物钻井液引起的地层伤害[J].探矿工程:岩土钻掘工程,2003(增刊1):261-263. Li Yunbo,Wu Xiaoming,Cai Jihua.Use biologic enzyme to alleviate the damage by polymer drilling fluid[J].Exploration Engineering:Rock & Soil Drilling and Tunneling,2003(supplement 1):261-263. |
| [3] |
路萍.复杂地质条件下储层损害机理与评价技术研究[D].荆州:长江大学,2013. Lu Ping.Reservoir damage mechanism and evaluation technology research under complicated geological conditions[D].Jingzhou:Yangtz University,2013. |
| [4] | Necmettin Mungan.Rheology and Adsorption of aqueous polymer solution[J].The Journal of Canadian Petroleum,1969,8(2):45-50. |
| [5] | Cohen Yoram,Christ F R.Polymer retention and adsorption in the flow of polymer solutions through porous media[R].SPE 12942,1986. |
| [6] | Zaitoun A,Chauvetear G.Effect of structure and residual oil on polymer bridging adsorption[R].SPE 39674,1998. |
| [7] | Zitha P L J,Darwish M M I.Effect of bridging adsorption on the placement of gels for water control[R].SPE 57269,1999. |
| [8] | Zaitoun A,Chauvetear G.Effect of structure and residual oil on polymer bridging adsorption[R].SPE 39674,1998. |
| [9] | Zitha P L J,van Os K G S,Denys K F J.Adsorption of linear flexible polymers during laminar flow through porous media:effect of the concentration[R].SPE 39675,1998. |
| [10] | Ogunberu A L,Asghari K.Water permeability reduction under flow-induced polymer adsorption[J].Journal of Canadian Petroleum Technology,2005,44(11):56-61. |
| [11] |
Civan F.油层伤害:原理、模拟、评价和防治[M].杨凤丽,译.北京:石油工业出版社,2003. Civan F.Reservoir damage:principle,simulation,evaluation and control[M].Translator:Yang Fengli.Beijing:Petroleum Industry Press,2003. |


