2. 北京信息科技大学, 北京 100192;
3. 中国石油辽河油田公司茨榆坨采油厂, 辽宁辽中 110206
2. Beijing Information Science & Technology University, Beijing, 100192, China;
3. Ciyutuo Oil Production Plant, PetroChina Liaohe Oilfield Company, Liaozhong, Liaoning, 110206, China
当前在深层、超深层油气资源勘探开发中面临着诸多理论和技术难题[1],主要表现在:高温高压环境下,环空温度、压力预测难度大,井底压力控制困难;气侵时井筒中往往呈现气液固多相流,流动规律复杂;安全密度窗口窄,易出现漏、溢及卡钻等井下故障。归根结底,核心问题在于对高温高压条件下环空多相流的流动特性认识不清,无法准确掌握环空温度和压力的变化规律,因此,开展深井、超深井多相流水力学模拟是必要的。井筒温度场和压力场相互影响,循环温度、压力的变化均会引起井筒流体热物性参数和流动参数改变,模型求解需要耦合迭代,其涉及井筒水力学、多相流以及传热学等多学科交融。目前,国内外学者针对井筒温度压力场耦合进行了相关研究[2,3,4,5,6,7],但是已有研究均未基于瞬态温度、压力,同时忽略了钻井流体物性参数是随温度压力的变化而变化的,无法真实模拟高温高压条件下井筒温度压力场耦合变化规律。为此,笔者从质量、动量和能量守恒方程出发,建立了井筒多相流全瞬态温度压力场耦合模型,分析了环空多相流瞬态温度和压力耦合变化规律,以期为深井、超深井水力参数设计提供参考。
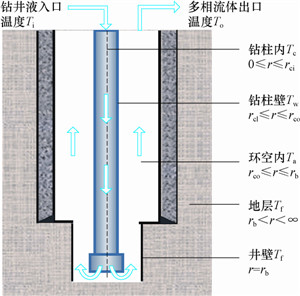
1 井筒物理模型在正常钻井作业中,钻井液以温度Ti由钻柱内进入,钻柱内充满钻井液,后经过钻头喷嘴进入环空,在井底混合天然气、岩屑上返,环空内为气液固多相流体,此时井底温度低于地层温度,多相流体不断从井壁岩石吸收热量,当多相流体达到某一井深时,其温度将大于地层温度,多相流体在上返过程中加热上部井壁岩石,最终多相流体以温度To由环空出口返出,如图 1所示。在这一过程中,钻柱内的流体、钻柱壁、环空内的流体、井壁、地层均会在轴向和径向上进行热能传递,钻柱内为单相传热,环空内为两相传热。随着井筒内热量的交换,循环流体的温度实时变化,从而影响井筒压力剖面,反过来井筒压力剖面的改变进一步影响井筒温度场,这是一个相互耦合的过程。
|
| 图 1 井筒物理模型 Fig. 1 Physical model of wellbore |
在建立井筒瞬态温度压力数学模型时,进行以下假设:1)钻井液在井筒内作一维流动,忽略径向变化;2)钻井液为水基钻井液,忽略天然气在钻井液中的溶解;3)钻柱、环空和地层均为非稳态传热,其中钻柱壁和井壁边界加入轴向热传导项;4)井筒内流体的轴向热传导与轴向热对流相比可以忽略不计;5)考虑岩屑对于井筒温度和压力的影响。
2.2 质量守恒方程气相、液相和固相的质量守恒方程分别为:
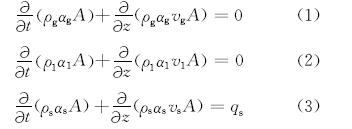
式中:A为流道面积,m2;ρg,ρl和ρs分别为气相、钻井液、岩屑的密度,kg/m3;αg,αl和αs分别为气相、钻井液、岩屑的体积分数;vg,vl和vs分别为气相、钻井液、岩屑的实际流速,m/s;qs为单位厚度岩屑产生速度,kg/(s·m)。
2.3 动量守恒方程动量守恒方程为:

式中:g为重力加速度,m/s2;pfa为环空内多相流摩阻压降,Pa。
根据文献[8,9,10]的研究成果,垂直环空气液两相流的流型可划分为泡状流、分散泡状流、段塞流、搅动流和环状流5类。2003年,C.Perez-Tellez[11]主要针对段塞流进行了压力梯度预测模型的修正(记为Perez模型),并将数值计算结果与路易斯安那大学全尺寸试验井的试验数据进行了对比,井筒压力平均误差不大于3.3%。因此,气液两相流压降计算采用高精度的Perez模型。
2.4 井筒温度数学模型钻井液正常循环期间,地层与环空钻井液进行热交换,环空钻井液与钻柱内钻井液进行热交换,钻井液在井内的整个循环过程可以看作是一个具有一定边界条件的热交换器。如图 1所示,井筒温度数学模型在径向具体可以分为5部分,分别为钻柱内、钻杆壁、环空、套管和地层。根据能量守恒原理,得到各组分的温度方程。
钻柱内流体的温度方程为:
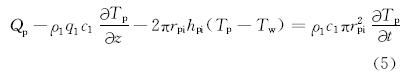
钻柱壁的温度方程为:
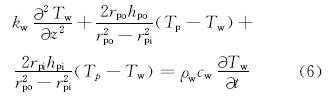
环空内流体的温度方程为:
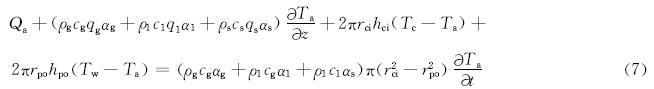
井壁的温度方程为:
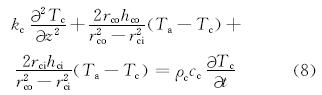
地层的温度方程为:
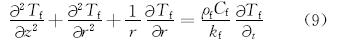
式中:ρ为密度,kg/m3;q为流体流量,L/s;Q为井筒摩擦力功率,W/m;T为温度,K;h为对流换热系数,W/(m2·K);k为导热系数,W/(m·K);c为比热容,J/(kg·K);z为轴向坐标,m;r为径向坐标,m。下标:l为液相;g为气相;p为钻柱;w为钻柱壁;a为环空;c为套管;f为地层;pi为钻柱内壁;po为钻柱外壁;ci为套管内壁;co为套管外壁。
气液两相流对流换热系数的计算与单相流相比有很大的差异,为了满足现场对精度的要求,选取不同流型下与试验数据相比误差较低的气液两相对流换热经验公式[12,13]。在垂直流动过程中,对于泡状流,建议采用Aggour模型;对于分散泡状流,建议采用Knott等人的模型;对于段塞流和搅拌流,建议采用Rezkallah-Sims模型;对于环状流,建议采用Ravipudi-Gobold模型。
2.5 辅助参数求解 2.5.1 天然气的黏度、比热容和导热系数黏度、比热容和导热系数等热物性参数均是温度、压力的函数,温度和压力变化时,它们亦随之改变。为了保证井筒温度、压力计算的准确性,分别采用与试验数据吻合较好的A.L.Lee[14]、D.G.Friend[15]、A.K.Lateef[16]等人提出的方法计算天然气的黏度、比热容和导热系数。
2.5.2 天然气和钻井液的表面张力表面张力在多相流计算中非常重要,对环空中气相的滑脱速度和对流换热系数均有影响。与现有模型相比,Sutton模型[17]的计算精度最高,因此,天然气和水基钻井液的表面张力采用该模型计算。
2.5.3 钻井液物性参数深井井筒处于高温、高压环境下,此时钻井液的密度/塑性黏度不再是常数。笔者采用解析法推导钻井液物性参数(密度、塑性黏度)与温度、压力的关系式。根据W.C.McMordie Jr.等人[18]通过试验测出的不同温度、压力下水基钻井液的密度,拟合出水基钻井液密度与温度、压力关系式的系数bp,bpp,bT,bTT和bpT分别为4.922 4×10-10,-9.687 7×10-19,-3.219 6×10-4,-1.743 2×10-6和4.918 6×10-13。同理可拟合出水基钻井液的塑性黏度表达式。

式中:p0为地面压力,MPa;T0为地面温度,K;ρ(p,T)为压力p和温度T下钻井液的密度,kg/m3;μ(p,T)为压力p和温度T下钻井液的塑性黏度,mPa·s。
3 多相流瞬态温度压力场耦合求解 3.1 边界条件钻井液注入温度和地表温度已知,作为井筒温度边界条件。同时,整个钻井过程中,井口回压维持不变,作为井筒压力边界条件。
3.2 模型离散井筒多相流瞬态温度压力场耦合求解的先决条件是实现井筒瞬态温度、压力的独立求解。井筒瞬态温度和压力模型的求解分别采用Crank-Nicolson全隐式格式[19]、以及四点差分显式格式[20],网格划分时选用定轴向、定时间及变径向网格。
针对井筒瞬态温度模型的全隐式处理,控制方程中的一阶空间导数采用一阶迎风格式,一阶时间导数采用两点向后差分,二阶空间导数采用三点中心差分。以此原则将井筒温度模型离散化,给出相应的有限差分格式。
钻柱内温度模型的有限差分格式为:
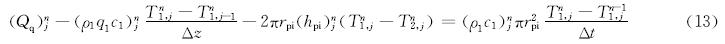
钻柱壁处温度模型的有限差分格式为:
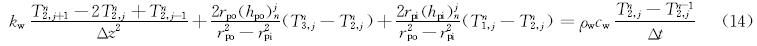
环空内温度模型的有限差分格式为:
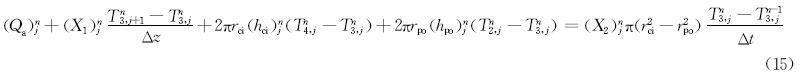
井壁处温度模型的有限差分格式为:
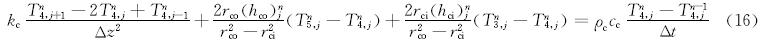
地层温度模型的有限差分格式为:
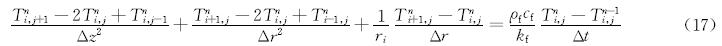
其中
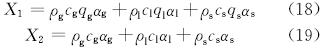
针对井筒瞬态压力模型的显式处理,控制方程中的一阶空间导数采用一阶迎风格式,一阶时间导数采用四点中心差分。以此原则将井筒压力模型离散化,给出相应的有限差分格式。
液相压力模型的有限差分格式为:
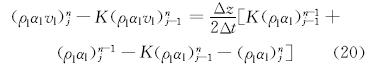
气相压力模型的有限差分格式为:
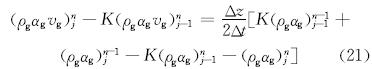
固相压力模型的有限差分格式为:
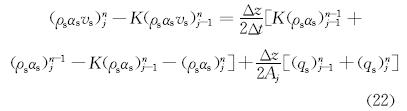
动量守恒方程的有限差分格式为:
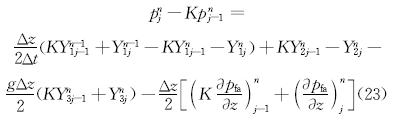
其中
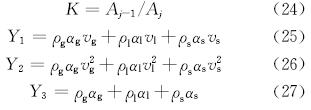
通过迭代方式对井筒多相流瞬态温度压力场耦合模型进行求解,具体步骤如下:1)针对井筒划分网格,在时间和空间上进行离散化处理;2)已知的地层温度作为井筒初始温度,代入井筒压力计算中,将稳态压力计算结果作为初始压力,同时给出井筒各组分流体的热物性参数以及体积分数;3)根据初始时刻的计算值,预估t=t0+Δt时刻的井筒温度Tj0、压力pj0以及各组分流体热物性参数和体积分数,代入瞬态温度模型计算t=t0+Δt时刻的井筒温度Tj;4)将t=t0+Δt时刻的井筒循环温度代入瞬态压力模型;5)求解环空内单点参数时,需要先后估算节点压力和气相体积分数;6)节点循环至井口,判断计算的井口回压是否满足精度要求,不满足时返回4)进行校正计算,直至得到满足精度要求的井筒压力pj;7)判断井筒环空压力和温度是否满足精度要求,即‖pj-pj0‖<εp且‖Tj-Tj(0)‖<εT,不满足则返回3)重新进行校正计算;8)t=t0+Δt时刻计算完毕,耦合迭代计算进入下一时刻。
4 算例分析利用上述井筒多相流瞬态温度压力场耦合模型,采用迭代求解算法,对塔里木油田某深井的井筒瞬态温度压力耦合变化规律进行了分析。由于已探明储层中不含有H2S等酸性气体,因此,求解过程中将侵入气体看作纯甲烷气体。计算时用到的基础参数为:井深6 500.00 m;套管内径157.0 mm,套管下深5 500.00 mm;钻头直径152.4 mm;钻杆外径88.9 mm,钻杆内径70.2 mm;喷嘴面积233 mm2;循环排量12 L/s;气侵量0.6 m3/s;机械钻速2.7 m/h;井口回压1 MPa;地表温度25 ℃;地温梯度0.03 ℃/m;钻井液的地面密度1 500 kg/m3,比热容3 900 J/(kg·K),导热系数1.73 W/(m·K),入口温度40 ℃;钻柱的密度7 800 kg/m3,比热容400 J/(kg·K),导热系数43.75 W/(m·K);水泥的密度1 900 kg/m3,比热容2 000 J/(kg·K),导热系数1 W/(m·K);岩石的密度2 640 kg/m3,比热容837 J/(kg·K),导热系数2.25 W/(m·K)。
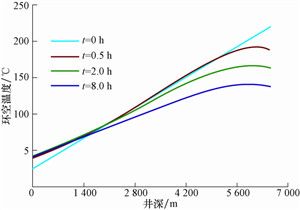
4.1 环空温度剖面图 2为计算出的不同循环时间下的环空温度剖面,图中t=0时刻的环空温度即为初始地层温度。
|
| 图 2 不同循环时间下的环空温度剖面 Fig. 2 Annular temperature over circulating time |
由图 2可知,环空内多相流体温度的大体规律为:环空井底温度低于地层温度,随着井深减小逐渐降低,径向强制对流换热能量由地层指向环空;当井深达到临界井深(约1 500 m)时,环空温度开始高于地层温度,环空-地层径向能量交换反向;环空多相流体循环最高温度处距离井底的距离为井深的十分之一(井深6 000 m附近),而环空单相钻井液循环最高温度处距离井底的距离为井深的1/7~1/6,这主要是由气液两相和单相对流换热系数的差异所导致的。
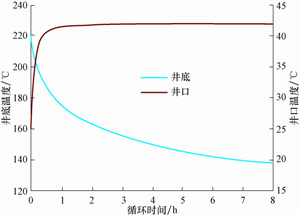
图 3为计算出的不同循环时间下的井口和井底温度。
|
| 图 3 不同循环时间下的井口和井底温度 Fig. 3 Wellhead and bottomhole temperatures over circulating time |
由图 3可知:随着循环时间增长,井底温度逐渐降低,且降低幅度逐渐变小;井口温度随循环时间增长而升高,且初期升高幅度大,但快速趋于稳定。原因是,近井口段气体膨胀最为明显,两相流由泡状流转换为段塞流,环空钻井液与钻杆外壁及井壁之间的对流换热系数快速增大,导致近井口段微元控制体径向换热充分,井口温度变化迅速趋于平衡。
4.2 岩屑运移速度剖面图 4为计算出的不同循环时间下的岩屑运移速度剖面。
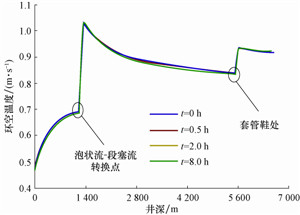
|
| 图 4 不同循环时间下的岩屑运移速度剖面 Fig. 4 Cuttings migration velocity over circulating time |
由图 4可知,岩屑运移速度分别在井深5 500.00和1 200.00 m处变化最为明显,发生阶跃现象。井深5 500.00 m为套管鞋处,此处环空流道面积突然增加,岩屑运移流速突然降低;此后随着井深减小,岩屑流速逐渐升高,原因是在该井段气液两相流流型为泡状流,而泡状流有利于携岩[21],因而岩屑运移速度逐渐升高;直至井深1 200.00 m处,岩屑运移速度突然降低,且随着井深减小,岩屑流速继续降低。这是因为此处为泡状流-段塞流转换点,在这里小气泡膨胀聚集形成大的泰勒气泡和液相段塞,而段塞流不利于携岩,因而岩屑流速降低。此外,从图 4还可以看出,随着循环时间增长,岩屑运移速度剖面变化较小,这也说明岩屑运移速度基本不受井筒循环温度的影响。
4.3 物性参数剖面图 5为计算出的不同循环时间下的钻井液密度剖面。
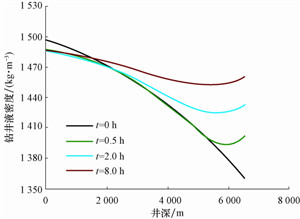
|
| 图 5 不同循环时间下的钻井液密度剖面 Fig. 5 Drilling fluid density over circulating time |
从图 5可以看出:随着循环时间增长,临界井深1 500.00 m以浅钻井液的密度逐渐增大,这是因为井筒环空循环温度逐渐降低,钻井液发生压缩,密度随之增大;当t=0时刻,即环空温度为地层温度,钻井液的密度随着井深增加逐渐降低。在循环温度影响下,随着井深增加,钻井液的密度先降低后升高,这是温度和压力对钻井液双重作用的结果;环空的最高温度在井深6 000.00m处,随着井深进一步增加环空温度降低,受温度降低和压力升高产生压缩效应的影响,钻井液的密度反而升高。
图 6为计算出的不同循环时间下的钻井液塑性黏度剖面。

|
| 图 6 不同循环时间下的钻井液塑性黏度剖面 Fig. 6 Drilling fluid plastic viscosity over circulating time |
从图 6可以看出:随着循环时间增长,临界井深1 500.00 m以浅钻井液的塑性黏度逐渐增大;当t=0时刻,即环空温度为地层温度,钻井液的塑性黏度随着井深增加逐渐降低;在循环温度的影响下,随着井深增加,钻井液的塑性黏度先降低后升高。
从图 5和图 6可以看出,循环8 h后环空井底钻井液的密度由1 360 kg/m3增至1 460 kg/m3,塑性黏度由8.6 mPa·s增至13.8 mPa·s。由以上分析可知,钻井液的物性参数(密度、塑性黏度)受井筒循环温度的影响较大,在建立高温高压井水力学模型时,需要充分考虑钻井液密度和塑性黏度的变化,进而准确计算井筒压力和温度,为现场钻井作业提供可靠的参数。
4.4 井底压力动态变化特征图 7为计算出的不同循环时间下的井底压力。
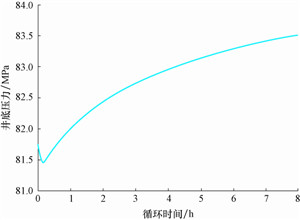
|
| 图 7 不同循环时间下的井底压力 Fig. 7 Bottomhole pressure over circulating time |
由图 7可知:随着循环时间增长,井底压力先迅速降低后逐渐升高,且升高幅度逐渐变小,井底压力渐趋于稳定;在循环时间为0~0.2 h时,井底压力呈线性降低,而在0.2 h以后井底压力呈对数升高。这是因为在循环初期,相比初始地层温度,整个环空温度大多升高且变化幅值较大,仅近井底段环空温度降低,井底压力受井筒环空温度升高的影响逐渐降低。当循环时间达到0.2 h后,环空近井底段温度继续下降,而近井口段温度升高且快速趋于稳定,这样井底压力受近井底段环空温度降低的影响逐渐增大。
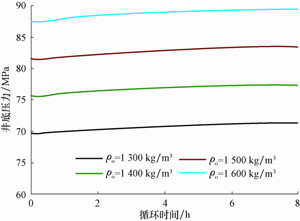
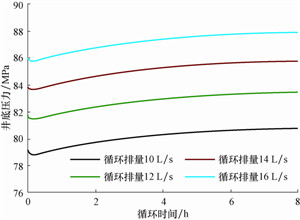
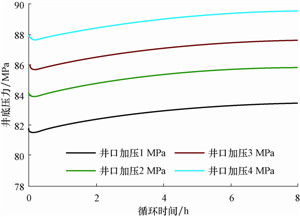
4.5 井底压力变化敏感性参数分析图 8—图 12分别为计算出的不同气侵量、钻井液地面密度、钻井液地面塑性黏度、循环排量、井口回压下井底压力随循环时间的变化曲线。
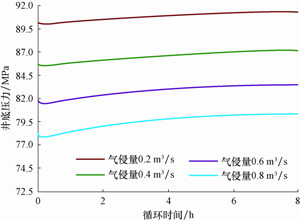
|
| 图 8 不同气侵量下井底压力与循环时间的关系 Fig. 8 Bottomhole pressure vs. circulating time at different gas influxes |
|
| 图 9 不同钻井液密度下井底压力与循环时间的关系 Fig. 9 Bottomhole pressure vs. circulating time at different drilling fluid densities |

|
| 图 10 不同钻井液塑性黏度下井底压力与循环时间的关系 Fig. 10 Bottomhole pressure vs. circulating time at different drilling fluid plastic viscosities |
|
| 图 11 不同循环排量下井底压力与循环时间的关系 Fig. 11 Bottomhole pressure vs. circulating time at different circulating displacements |
|
| 图 12 不同井口回压下井底压力与循环时间的关系 Fig. 12 Bottomhole pressure vs. circulating time under different wellhead back pressures |
从图 8—图 12可以看出,井底压力随钻井液的地面密度和塑性黏度,循环排量、井口回压增大而增大,而井底压力随气侵量增大而减小。对比循环8 h后气侵量、钻井液的地面密度和塑性黏度、循环排量和井口回压对井底压力的影响,可知当气侵量从0.2 m3/s升至0.8 m3/s循环8 h后井底压力变化值升高1.2 MPa,钻井液地面密度从1 300 kg/m3升至1 600 kg/m3时升高0.4 MPa,钻井液地面塑性黏度从20 mPa·s升至50 mPa·s时仅升高0.04 MPa,排量从10 L/s升至16 L/s时升高0.2 MPa,井口回压从1.0 MPa升至4.0 MPa时降低0.2 MPa。由此可知,气侵量对井底压力的影响最大,钻井液地面密度、排量、井口回压次之,钻井液地面塑性黏度最小。根据不同参数对井底压力的影响程度, 在钻井过程中,可以通过优化排量和钻井液地面密度以及施加一定的井口回压,使井底压力位于安全窗口之内的同时,尽可能降低由循环温度变化引起的井底压力波动,降低钻井作业风险。
5 结 论1) 基于井筒多相流、传热学理论,充分考虑循环流体物性参数随温度压力的变化,建立了适用于深井、超深井的井筒多相流全瞬态温度压力场耦合模型,并提出了迭代求解算法,保证了模型的稳定性和收敛性。
2) 环空多相流体最高循环温度位于距离井底十分之一处。随着循环时间增长,岩屑运移速度基本保持不变,而临界井深1 500.00 m以浅钻井液的密度/塑性黏度逐渐升高。随着井深增加,钻井液的密度、塑性黏度先降低后升高,钻井液密度增幅较大。
3) 井底压力随循环时间增长先呈线性降低后呈对数升高。气侵量对井底压力的影响最大,钻井液地面密度、排量、井口回压次之,钻井液地面塑性黏度最小。
4 ) 钻井过程中,适当降低排量和钻井液密度以及施加一定的井口回压,可以有效降低井底压力波动,确保将井底压力维持在安全窗口之内,从而降低钻井作业风险。
| [1] |
曾义金,刘建立.深井超深井钻井技术现状和发展趋势[J].石油钻探技术,2005,33(5):1-5. Zeng Yijin,Liu Jianli.Technical status and developmental trend of drilling techniques in deep and ultra-deep wells[J].Petroleum Drilling Techniques,2005,33(5):1-5. |
| [2] |
李根生,窦亮彬,田守嶒,等.酸性气体侵入井筒瞬态流动规律研究[J].石油钻探技术,2013,41(4):8-14. Li Gensheng,Dou Liangbin,Tian Shouceng,et al.Characteristics of wellbore transient flow during sour gas influx[J].Petroleum Drilling Techniques,2013,41(4):8-14. |
| [3] |
吴晓东,王庆,何岩峰.考虑相态变化的注CO2井井筒温度压力场耦合计算模型[J].中国石油大学学报:自然科学版,2009,33(1):73-77. Wu Xiaodong,Wang Qing,He Yanfeng.Temperature-pressure field coupling calculation model considering phase behavior change in CO2 injection well borehole[J].Journal of China University of Petroleum:Edition of Natural Science,2009,33(1):73-77. |
| [4] |
宋洵成,韦龙贵,何连,等.气液两相流循环温度和压力预测耦合模型[J].石油钻采工艺,2012,34(6):5-9. Song Xuncheng,Wei Longgui,He Lian,et al.A coupled model for wellbore temperature and pressure prediction of gas-liquid drilling fluid[J].Oil Drilling & Production Technology,2012,34(6):5-9. |
| [5] |
陈林,孙雷,彭彩珍,等.注CO2井筒温度场分布规律模拟研究[J].断块油气田,2009,16(6):82-84. Chen Lin,Sun Lei,Peng Caizhen,et al.Simulation of temperature field for CO2 injection well bore[J].Fault-Block Oil & Gas Field,2009,16(6):82-84. |
| [6] | Hasan A R,Kabir C S,Wang Xiaowei.Wellbore two-phase flow and heat transfer during transient testing[J].SPE Journal,1998,3(2):174-180. |
| [7] | Izgec B,Kabir C S,Zhu D,et al.Transient fluid and heat flow modeling in coupled wellbore/reservoir systems[J].SPE Reservoir Evaluation & Engineering,2007,10(3):294-301. |
| [8] | Caetano E F,Shoham O,Brill J P.Upward vertical two-phase flow through an annulus:part 2:modeling bubble,slug,and annular flow[J].Journal of Energy Resources Technology,1992,114(1):14-30. |
| [9] | Hasan A R,Kabir C S.A study of multiphase flow behavior in vertical wells[J].SPE Production Engineering,1988,3(2):263-272. |
| [10] | Lage A C V M,Time R W.Mechanistic model for upward two-phase flow in annuli[R].SPE 63127,2000. |
| [11] | Perez-Tellez C,Smith J R,Edwards J K.A new comprehensive,mechanistic model for underbalanced drilling improves wellbore pressure predictions[J].SPE Drilling & Completion,2003,18(3):199-208. |
| [12] | Gao Changhong.Empirical heat transfer model for slug flow and bubble flow in vertical subsea pipes[R].SPE 85651,2003. |
| [13] | Tang C C.A study of heat transfer in non-boiling two-phase gas-liquid flow in pipes for horizontal,slightly inclined,and vertical orientations[D].Stillwater:Oklahoma State University,2011. |
| [14] | Lee A L,Gonzalez M H,Eakin B E.The viscosity of natural gases[J].Journal of Petroleum Technology,1966,18(8):997-1000. |
| [15] | Friend D G,Roder H M.The thermal conductivity surface for mixtures of methane and ethane[J].International Journal of Thermophysics,1987,8(1):13-26. |
| [16] | Adewale Kareem Lateef,James Omeke.Specific heat capacity of natural gas;expressed as a function of its specific gravity and temperature[R].SPE 150808,2011. |
| [17] | Sutton R P.An improved model for water-hydrocarbon surface tension at reservoir conditions[R].SPE 124968,2009. |
| [18] | McMordie W C Jr,Bland R G,Hauser J M.Effect of temperature and pressure on the density of drilling fluids[R].SPE 11114,1982. |
| [19] |
李相方,管丛笑,隋秀香,等.环形井眼气液两相流流动规律研究[J].水动力学研究与进展:A辑,1998,13(4):422-429. Li Xiangfang,Guan Congxiao,Sui Xiuxiang,et al.Circular hole flow law of gas liquid two phase flow study[J].Journal of Hydrodynamics:A Serial,1998,13(4):422-429. |
| [20] |
李梦博,柳贡慧,李军,等.考虑非牛顿流体螺旋流动的钻井井筒温度场研究[J].石油钻探技术,2014,42(5):74-79. Li Mengbo,Liu Gonghui,Li Jun,et al.Research on wellbore temperature field with helical flow of non-Newtonian fluids in drilling operation[J].Petroleum Drilling Techniques,2014,42(5):74-79. |
| [21] |
何淼,柳贡慧,李军,等.气侵期间岩屑运移规律研究[J].科学技术与工程,2014,14(16):27-31. He Miao,Liu Gonghui,Li Jun,et al.The research of cuttings migration during gas invasion[J].Science Technology and Engineering,2014,14(16):27-31. |




