2. 海相储层演化与油气富集机理教育部重点实验室(中国地质大学(北京)), 北京 100083;
3. 页岩气资源战略评价国土资源部重点实验室(中国地质大学(北京)), 北京 100083;
4. 油气藏地质及开发工程国家重点实验室(成都理工大学), 四川成都 610059
2. Ministry of Education Key Laboratory for Marine Reservoir Evolution and Hydrocarbon Abundance Mechanism (China University of Geosciences (Beijing)), Beijing, 100083, China;
3. Key Laboratory for Shale Gas Exploitation and Assessment, Ministry of Land and Resources (China University of Geosciences (Beijing)), Beijing, 100083, China;
4. State Key Laboratory of Oil and Gas Reservoir Geology and Exploration (Chengdu University of Technology), Chengdu, Sichuan, 610059, China
三叠系致密砂岩储层是川西天然气勘探的重要储层[1],但该储层具有低孔、特低渗透性及强非均质性特征,部分地层还具有砂泥岩频繁互层的情况,复杂的地质特征对岩石微观结构特征、矿物学特征及地震资料反演等的研究造成了困难[2]。由于岩石矿物成分、颗粒构成、接触关系、流体成分及含气饱和度等方面的特征可以综合反映在岩石弹性参数上进行[3],因此对该目的层致密砂岩的弹性参数进行深入、精细的研究,对地层岩石矿物学、钻井完井工程及地震反演等都具有重要意义[4]。岩石的弹性参数包括弹性模量、体积模量、剪切模量及泊松比等[5],地层条件下岩石弹性模量及泊松比反映岩石的重要弹性特征,其精确预测对其他力学参数计算及应力场模拟等具有很大作用[6]。岩石弹性参数一般采用实验室静态力学测试结果与声波动态计算结果转换的方法,最终获得各井静态弹性参数。但该方法存在不足,即利用该方法解释动态弹性模量及泊松比时,横波测井资料必不可少,而常规测井一般只进行纵波测试,只有全波列测井才有横波测试结果。但是,对于各研究区域而言,往往纵波测井资料齐全,而横波测井资料仅为数不多的井才有;即使具有横波测试资料,地质条件复杂地层(如砂岩及泥页岩频繁互层)的横波测试资料可靠性往往也难以保证,因此采用预测的横波再预测静态弹性参数的误差就会更大。
Hoek-Brown准则(以下称为H-B准则)是E.Hoek和E.T.Brown于1980年提出的非线性岩石强度预测准则[7],该准则在预测岩石破裂、井壁稳定及边坡等方面均有重要应用价值[8]。基于此,笔者提出了一种仅利用纵波测井资料的岩石弹性参数解释新方法,并对实验室试验与常规解释方法进行了对比,对新方法的有效性进行了分析验证。
1 试验样品及方法致密砂岩及泥页岩试样取自川西三叠系地层, 埋深均大于3 000 m,采用高端显微镜进行观察分析,发现试样主要含石英砂岩、粉砂岩、岩屑砂岩及杂砂岩成分。取黑色泥页岩试样1组作为对比样,其主要成分为泥质、石英及炭屑,部分试样在显微镜下可以观察到泥质被方解石交代。试样尺寸及其他基本信息见表 1。
| 试样岩性 | 深度/m | 试样组数 | 试样个数 | 直径/mm | 长度/mm | 孔隙度,% |
| 致密砂岩 | 3 037~3 356 | 6 | 4 | 25 | 50 | 1.41~3.59 |
| 泥页岩 | 3 028~3 355 | 1 | 4 | 25 | 50 |
6 组砂岩试样编号为M1,M2,…,M6,1组泥页岩试样编号为N1。取心地层压力系数为1.6~2.0,垂向主应力与地层压力之差约为32 MPa,因此设试验每组4个试样的有效围压分别为0,12,22和32 MPa,试样饱和地层水。采用MTS岩石物理测试仪进行常规力学加载,压力传感器误差小于1%,应变量可精确到0.000 1 mm,超声波换能器频率为1 MHz。试验方案为:单轴测试以3.5×10-3/s轴向应变率加载至试样破坏;三轴测试以0.05 MPa/s加载围压至设定值,以3.5×10-3/s轴向应变率加载至试样破坏;各阶段声学数据通过岩石应力-应变曲线变化特征手动设置节点保存。
2 岩石应力应变阶段划分图 1所示为致密砂岩及泥页岩3个应变与轴向应力之间的关系。图 1中,正方向的应变表示不断压缩,负方向的应变表示膨胀。

|
| 图 1 试样在三轴条件下的应力-应变关系 Fig. 1 Triaxial stress-strain diagram of samples |
从图 1可以看出,所取砂岩及泥页岩在地层围压条件下其应力-应变关系大体类似,主要可分为4个阶段:1)初始压密段,对应砂岩从O到A(或泥页岩从O′到A′);2)线弹性变化阶段,对应砂岩从A到B(或泥页岩从A′到B′);3)塑性延展阶段,对应砂岩从B到C(或泥页岩从B′到C′),此时体积应变具有向负应变方向偏离的趋势;4)残余变形阶段,对应砂岩C点之后(或泥页岩C′之后),此时岩石已发生剪切破坏,只剩残余强度。
取心段地层部分差应变测试结果见表 2。从表 2可以看出,该地层三向主应力(总应力)大体为60~83 MPa,且满足垂向主应力>最大水平主应力>最小水平主应力,为正常应力系统。表 2中,测试样品均为砂岩,一般砂岩段应力值略小于泥页岩段,而砂岩轴向峰值应力要大于泥页岩轴向峰值应力(见图 1),对于地层围压条件下不同岩性试样弹性参数的取值点,大致位于1/2峰值应力处,该位置处于线弹性变化段。
| 试样岩性 | 垂深/m | 主应力/MPa | ||
| 最大水平 | 最小水平 | 垂向 | ||
| 砂岩 | 3 339 | 71.03 | 67.04 | 82.54 |
| 砂岩 | 3 028 | 64.50 | 61.89 | 74.49 |
由于常规声波测井频率为20 kHz,而试验声波波速为频率1 MHz条件下的测试值,因此进行测井解释前要进行声波衰减(频率)校正。具体方法为:以一般认为不发生声波衰减的铝样为参考样[9],获得铝样与试样在一定周期范围内较为完整的波形(见图 2);然后,在波形周期范围内将铝样及试样波形按不同频率进行分离,获得频谱图(见图 3);认为在主频1 MHz附近不同频率间声波波速的衰减近似服从线性关系(见图 4,图中R为相关系数),拟合线斜率即为频率转换间波速的衰减系数,提取主频1 MHz衰减系数并适当转换,可获得测试样品在20 kHz频率下的波速值,从而减小测井解释误差。

|
| 图 2 铝样与试样完整波形信号 Fig. 2 Full waveform signal of aluminium sample and tested samples |

|
| 图 3 铝样与试样频谱 Fig. 3 Spectrum diagram of aluminum and tested samples |

|
| 图 3 铝样与试样谱比 Fig. 4 Spectrum ratio diagram of aluminum and tested samples |
地质强度指数(geological strength inclex,GSI)[10]是H-B准则中重要的输入参数。GSI的确定有多种方法,如地质观察估值法、反算法及波速法等。一般来说,用各种方法确定的GSI应相差不大,笔者采用波速自洽方法求取GSI。在国内外岩石力学工程研究中,均有采用纵波波速对岩体质量指标进行分类的方案[11],因为纵波波速能够反映岩体的结构及强度特征,故笔者亦采用纵波波速值定义地质强度指标GSI,波速值采用按前述方法进行频率转化后的值。
由于笔者主要对岩石弹性参数中的弹性模量及泊松比进行研究,因此在保持弹性模量预测精度不降低的前提下利用自洽法预测GSI。H-B准则预测岩石等效弹性模量的公式为[12]:

通过不断调整GSI的值,将计算的Em值与线性段实测Em值进行对比,通过自洽确定最佳GSI值,使Em的预测误差最小。GSI取值见表 3。
| 试样组号 | GSI | Em/GPa | Em 的相对误差,% | |
| 实测 | 预测 | |||
| M1 | 83.2 | 42.12 | 42.49 | 0.88 |
| M2 | 79.0 | 29.59 | 32.41 | 9.53 |
| M3 | 82.0 | 41.01 | 40.21 | 1.95 |
| M4 | 80.0 | 39.87 | 42.36 | 6.25 |
| M5 | 78.0 | 35.77 | 34.87 | 2.52 |
| M6 | 90.0 | 58.51 | 56.94 | 2.68 |
从表 3可以看出,Em预测值与实测值的相对误差较小,结果可靠。
GSI与岩体强度间具有相关性[10]。GSI与地层围压条件下岩石抗压强度的关系如图 5所示。

|
| 图 5 地质强度指数与岩石三轴强度的关系 Fig. 5 Relationship between GSI and the rock triaxial strength |
从图 5可以看出,GSI与岩石三轴强度间具有较好的正相关性,对于强度最高的一组测试样品,其GSI值最大。但对于三轴强度在150~250 MPa的样品来说,两者间正相关性变弱,这主要是由于影响岩石三轴强度的因素较多,如孔隙度、孔隙密度、纵波波速、颗粒排列、微裂隙及泥质含量等,而笔者只根据纵波波速值定义GSI,该强度范围内的岩石三轴强度与GSI值间的正相关性偏弱表明岩石内部物理力学性质的复杂。三轴强度最高的一组样品在拟合关系中发挥了重要作用,整体而言R=0.826,拟合效果较好。同时,所取试样均为完整样,因此所计算试样的GSI值较大(>75)。
3.3 H-B准则中参数s,a和mb的定义H-B准则的原始表达式为[13]:



mb由小到大变化表示岩石由韧性逐渐转变为硬脆性;s和a的取值均为0~1,s可大体指示岩体节理等非连续构造发育程度,a可用来调节包络线曲率。
为了使获得的s,a及mb的数值范围合理,且不影响最终预测结果的精度,具体计算方法为:先利用前面计算的各组样品的GSI值及式(3)、式(4)分别计算出s和a;然后将各组样品实测的σ1,σ3,σc,s及a值代入式(2),获取最佳mb拟合值。H-B准则中,各参数的计算结果见表 4,单组样品在不同围压条件下的轴向峰值应力拟合效果见图 6。
| 试样组号 | a | mb | s |
| M1 | 0.500 438 | 28.97 | 0.154 6 |
| M2 | 0.500 593 | 18.15 | 0.108 4 |
| M3 | 0.500 648 | 29.76 | 0.097 0 |
| M4 | 0.500 492 | 30.84 | 0.135 3 |
| M5 | 0.500 201 | 47.23 | 0.329 2 |
| M6 | 0.500 707 | 26.47 | 0.086 8 |
从图 6可以看出,H-B准则较好地考虑了岩石在各级围压条件下峰值应力的非线性变化,拟合效果较好。对所求得的H-B参数(见表 4)进行讨论,作各参数与地层条件下的岩石三轴强度间关系(见图 7)。

|
| 图 6 M6试样轴向应力与围压的关系 Fig. 6 Relationship between axial stress and confining pressure |

|
| 图 7 H-B参数与岩石三轴强度的关系 Fig. 7 Relationship between H-B parameters and rock triaxial strength |
由图 7可知,mb和s与岩石三轴强度之间具有较好的正相关关系,相关系数分别为R=0.883和R=0.823;a与岩石三轴强度之间具有一定负相关关系,R=0.811;其中,mb与岩石三轴强度之间的相关性最好,R=0.883。参数mb的含义明确,在地层较高围压条件下,较高的mb值往往代表岩石具有较高的硬度及强度,因此也具有相对较高的抗压强度。同时发现,mb与s之间具有较好的正相关性(R=0.884),因此可以利用s对mb值进行预测,这样也避免了H-B准则中mi值[11]的引入,简化了计算过程。
3.4 岩石弹性模量解释利用式(1)对岩石的弹性模量进行测井解释的关键是岩石单轴抗压强度及地质强度指数的计算。由于研究发现地质强度指数及纵波波速值均与岩石三轴强度具有较好的相关性,因此考虑利用纵波波速值对岩石地质强度指数进行解释,结果见图 8。

|
| 图 8 试样地质强度指数与纵波波速的关系 Fig. 8 Relationship of GSI and longitudinal wave velocity |
对岩石单轴抗压强度进行解释,发现随着试样三轴强度的升高,单轴强度具有降低趋势(见图 9)。分析认为与岩石内部颗粒排列及微组构有关,不同岩石具有不同的σ1-σ3变化样式,随着σ3的升高,轴向应力σ1会升高。但当岩石内部组分及结构不同时,σ1随σ3增加而升高的幅度是不相同的,以M2及M5组试样为例,这2组试样的σ1-σ3变化样式及显微图像见图 10。

|
| 图 9 试样单轴抗压强度与三轴强度的关系 Fig. 9 Relationship between rock triaxial strength and rock uniaxial compressive strength |
M2组试样在地层围压条件下测得的三轴强度值最高,而单轴强度值最低;M5组试样在地层围压条件下测得的三轴强度值最低,而单轴强度值最高。M2组试样为粉砂岩,在显微镜下观察岩石具有微—粉砂状结构(见图 10),碎屑以石英粉砂为主,占84%,分选性差,圆度差,岩屑以云母和炭屑为主,炭屑呈粒状、线状及条带状。这些因素导致其轴向应力随围压的升高变化幅度减小,随着围压的升高,内部炭屑等物质会变形及产生微裂缝。而在单轴条件下,粉砂结构使其内部组分间较为紧密地联系在一起,因此单轴强度较高。M5组试样为杂砂岩,显微镜下观察岩石具有不等粒砂状结构,粗—中砂及粉砂形成“双峰态”分布(见图 10)。碎屑主要成分为石英和岩屑,岩屑以燧石岩屑为主(占15%),填隙物主要为泥质杂基,与粉砂混合,构成基底式胶结,岩石较致密,未见孔缝。这些组分及致密结构特征造成其轴向应力随围压升高而大幅度增大;但在单轴条件下,由于没有围压,在轴向应力作用下不同粒度颗粒之间可形成弱面,易产生滑脱及剪切破坏[14],从而造成单轴条件下的强度较低。因此,川西致密砂岩单轴强度与三轴强度之间呈现一定负相关。

|
| 图 10 M2及M5组试样σ1-σ3变化样式及显微图像 Fig. 10 The change style of σ1-σ3 and microscope image of M2 and M5 samples |
研究GSI,mb,a及s与σc的相关性发现,对于所取致密砂岩样品,a与σc之间正相关,而GSI,mb及s与σc之间负相关,由于主要根据地层条件下的纵波波速确定GSI,因此负相关的原因与前面类似。mb的确定综合考虑了各级围压条件,且最终发现该参数与σc之间相关性最好(见图 11),因此可以利用mb来预测σc。mb由低到高表示岩石逐渐由韧性转变为脆性,单轴强度随mb增大而略微发生降低,表明该参数考虑了不同岩性砂岩内部结构及粒度的变化,该变化规律在川西如图 10所示岩石颗粒变化特征的致密砂岩中是适用的。

|
| 图 11 mb与σc之间的关系 Fig. 11 Relationship between mb and σc |
图 12为地层条件下所取致密砂岩及泥页岩在线性段的应变关系,分别对应图 1中M2组砂岩AB段和N1组泥页岩A′B′段。

|
| 图 12 试样环向应变与轴向应变的关系 Fig. 12 Relationship between the circumferential and axial strains of samples |
从图 12可以看出,该段线性拟合关系非常好,此时斜率为泊松比,为一定值,2组样品泊松比分别为0.306和0.380,由于饱和地层水,致密砂岩泊松比略微偏高(超声测试的泊松比为0.272)。
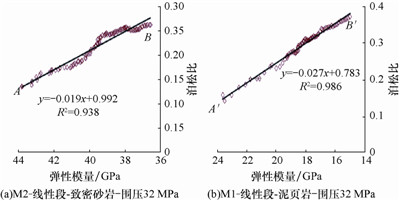
实际上,当对每个加载点的环向应变及轴向应变分别作对比,泊松比与弹性模量间的关系如图 13所示。
|
| 图 13 试样弹性模量与泊松比的关系 Fig. 13 Relationship between Em and Poisson's Ratio of samples |
从图 13可以看出,在2种岩性线的弹性段中,泊松比随着加载的进行逐渐升高。分析认为,这是因为岩石的轴向及环向应变都非常小,每2个数据值间的时间间隔仅约3 s,应变量可小于0.5×10-4 mm,因此很难根据图 12中的斜率对泊松比进行准确求取,M2组致密砂岩最终泊松比取值为0.239。图 13表明,在岩组石应力-应变线性段中,泊松比与弹性模量具有较好的相关性,因此针对某一地区的试样,在模拟地层测试条件下,根据确定的弹性模量对泊松比进行取值或预测是适用的。
地层条件下岩石弹性模量与泊松比的关系如图 14所示,可以看出,两者的相关性非常好。

|
| 图 14 试样弹性模量与泊松比的关系 Fig. 14 Relationship between Em and Poisson's Ratio |
通过利用纵波波速对GSI进行解释,利用GSI对s进行解释,利用s对mb进行解释,最终利用mb对σc进行解释,将解释结果代入式(1),完成对Em的测井解释。Em最终的测井解释结果见表 5。
| 试样组号 | Em/GPa | 相对误差,% | |
| 实测值 | 测井解释值 | ||
| M1 | 42.12 | 43.05 | 2.21 |
| M2 | 29.59 | 31.90 | 7.81 |
| M3 | 41.01 | 39.82 | 2.90 |
| M4 | 39.87 | 34.49 | 13.49 |
| M5 | 35.77 | 39.82 | 11.32 |
| M6 | 58.51 | 57.76 | 1.28 |
| 平均 | 6.50 | ||
由表 5可知,由于M4及M5组试样的Em基数较小,因而相对误差略微偏大,但从整体解释效果及绝对误差来看,能够满足工程需要。
采用动、静态参数转化方法,根据实测Em值对声学计算值进行校正,转换方程为Ems=1.131Emd-17.14,R2=0.761,最终结果见表 6。对比表 5和表 6可以看出,无论是最大相对误差还是平均相对误差,基于H-B准则的解释结果都要好一些。
| 试样组号 | Em/GPa | 相对误差,% | |
| 实测值 | 测井解释值 | ||
| M1 | 42.12 | 36.03 | 14.46 |
| M2 | 29.59 | 30.21 | 2.10 |
| M3 | 41.01 | 42.95 | 4.73 |
| M4 | 39.87 | 38.93 | 2.36 |
| M5 | 35.77 | 43.37 | 21.25 |
| M6 | 58.51 | 55.15 | 5.74 |
| 平均 | 8.44 | ||
利用前述新方法,根据地层围压测试条件下的弹性模量对泊松比进行预测,预测结果见图 14。同时,与利用校正后的声波波速及常规动静转换关系(见图 15)获得的泊松比值进行对比,对比结果见表 7。对比发现,常规方法的平均相对误差为5.78%,新方法的平均相对误差为5.55%,2种方法解释结果相差不大,表明2种方法都是可行的。

|
| 图 15 试样动静态泊松比关系 Fig. 15 Relationship between the dynamic and static Poisson's Ratio of samples |
| 试样组号 | 泊松比实测值 | 泊松比解释值 | 相对误差,% | ||
| 常规方法 | 新方法 | 常规方法 | 新方法 | ||
| M2 | 0.286 | 0.290 | 0.274 | 1.40 | 4.20 |
| M3 | 0.244 | 0.216 | 0.240 | 11.48 | 1.64 |
| M4 | 0.213 | 0.221 | 0.243 | 3.76 | 14.08 |
| M5 | 0.241 | 0.239 | 0.256 | 0.83 | 6.22 |
| M6 | 0.184 | 0.205 | 0.187 | 11.41 | 1.63 |
| 平均 | 5.78 | 5.55 | |||
利用上述新的解释方法,建立基于H-B准则单井弹性参数及所定义参数的测井解释剖面,同时与常规解释结果进行对比,结果见图 16。

|
| 图 16 单井弹性参数测井解释成果 Fig. 16 Log interpretation profile of elasticity parameters of single well |
从图 16可以看出,基于H-B准则的新方法解释的Em变化趋势与常规方法解释结果基本一致,两者相对误差为5%~35%,相对误差较大的主要原因是由于砂泥岩频繁互层引起的,一般泥岩的Em值较小,导致其相对误差较大;从绝对误差来看,2种方法的解释结果相差不大。对于泊松比,2种方法的解释结果变化趋势也大体相同,但在高泥质含量段,新方法的解释值要略低于常规方法的解释值;从相对误差及绝对误差来看,2种方法解释的泊松比值极为接近,彼此相差不大。以上对比结果表明,笔者基于H-B准则提出的岩石弹性参数测井解释方法可行,结果可靠,具有一定的工程应用价值,同时该方法在进行弹性参数解释时不需要用到横波时差资料。
5 结 论1) 川西三叠系取心段致密砂岩及泥页岩试样的应力-应变特征较为类似,可划分初始压密、线弹性变化、塑性延展和残余变形等4个阶段。
2 ) 基于H-B准则对岩石弹性参数中的弹性模量和泊松比进行了解释,与常规方法对比表明,基于H-B准则的解释方法误差更小;同时建立了单井弹性参数测井解释剖面,2种方法弹性参数解释结果变化趋势较为一致,可为工程施工提供依据。
3) 常规弹性参数测井解释在进行动静校正时需要用到横波时差,而笔者提出的方法不需要横波时差,因此该方法在缺少横波测井资料或横波资料不可靠时优势明显。
4 ) 要注意的是,将利用笔者提出的新方法解释的弹性参数结果,与具有可靠横波测井资料采用常规解释方法的井的解释结果进行对比,在获得较小误差的前提下,方可应用到其他没有横波测试的各井中。
| [1] |
蒋祖军, 肖国益, 李群生.川西深井提高钻井速度配套技术[J].石油钻探技术, 2010, 38(4):30-34. Jiang Zujun, Xiao Guoyi, Li Qunsheng.Technology to increase deep well drilling speed in Western Sichuan[J].Petroleum Drilling Techniques, 2010, 38(4):30-34. |
| [2] | Ruiz F, Cheng A.A rock physics model for tight gas sand[J].The Leading Edge, 2010, 29(12):1484-1489. |
| [3] |
陆黄生.测井技术在石油工程中的应用分析与发展思考[J].石油钻探技术, 2012, 40(6):1-7. Lu Huangsheng.Application and development analysis of well logging information in petroleum engineering[J].Petroleum Drilling Techniques, 2012, 40(6):1-7. |
| [4] |
曾义金.页岩气开发的地质与工程一体化技术[J].石油钻探技术, 2014, 42(1):1-6. Zeng Yijin.Integration technology of geology & engineering for shale gas development[J].Petroleum Drilling Techniques, 2014, 42(1):1-6. |
| [5] |
路保平, 鲍洪志.岩石力学参数求取方法进展[J].石油钻探技术, 2005, 33(5):44-47. Lu Baoping, Bao Hongzhi.Advances in calculation methods for rock mechanics parameters[J].Petroleum Drilling Techniques, 2005, 33(5):44-47. |
| [6] | Liu Zhiguang, Chen Jianyun, Bai Weifeng, et al.Improved parameter selection method for mesoscopic numerical simulation test of direct tensile failure of rock and concrete[J].Journal of Central South University of Technology, 2010, 17(5):1079-1086. |
| [7] | Hoek E, Marinos P G, Marinos V P.Characterisation and engineering properties of tectonically undisturbed but lithologically varied sedimentary rock masses[J].International Journal of Rock Mechanics and Mining Sciences, 2005, 42(2):277-285. |
| [8] |
申瑞臣, 屈平, 杨恒林.煤层井壁稳定技术研究进展与发展趋势[J].石油钻探技术, 2010, 38(3):1-7. Shen Ruichen, Qu Ping, Yang Henglin.Advancement and development of coal bed wellbore stability technology[J].Petroleum Drilling Techniques, 2010, 38(3):1-7. |
| [9] |
张元中, 楚泽涵, 李铭, 等.岩石声频散的实验研究及声波速度的外推[J].地球物理学报, 2001, 44(1):103-111. Zhang Yuanzhong, Chu Zehan, Li Ming, et al.An experimental study of acoustic dispersion of rock and extrapolation of the velocity[J].Chinese Journal of Geophysics, 2001, 44(1):103-111. |
| [10] | Marinos V, Marinos P, Hoek E.The geological strength index:applications and limitations[J].Bulletin of Engineering Geology and the Environment, 2005, 64(1):55-65. |
| [11] |
夏开宗, 陈从新, 刘秀敏, 等.基于岩体波速的 Hoek-Brown 准则预测岩体力学参数方法及工程应用[J].岩石力学与工程学报, 2013, 32(7):1458-1466. Xia Kaizong, Chen Congxin, Liu Xiumin, et al.Estimation of rock mass mechanical parameters based on ultrasonic velocity of rock mass and Hoek-Brown Criterion and its application to engineering[J].Chinese Journal of Rock Mechanics and Engineering, 2013, 32(7):1458-1466. |
| [12] |
闫长斌, 徐国元.对Hoek-Brown公式的改进及其工程应用[J].岩石力学与工程学报, 2005, 24(22):4030-4035. Yan Changbin, Xu Guoyuan.Modification of Hoek-Brown expressions and its application to engineering[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(22):4030-4035. |
| [13] |
廖异, 曾祥国, 符文熹, 等.Hoek-Brown岩体非线性强度的线性化方法[J].中南大学学报:自然科学版, 2012, 43(12):4902-4911. Liao Yi, Zeng Xiangguo, Fu Wenxi, et al.Linearization method of non-linear strength of Hoek-Brown rock mass[J].Journal of Central South University:Science and Technology, 2012, 43(12):4902-4911. |
| [14] | Alkan H, Cinar Y, Pusch G.Rock salt dilatancy boundary from combined acoustic emission and triaxial compression tests[J].International Journal of Rock Mechanics and Mining Sciences, 2007, 44(1):108-119. |



